泰勒公式学习笔记

泰勒公式学习笔记

这里可能只是对泰勒公式的粗略理解，具体还要等我把普林斯顿微积分读本看完。

本笔记参考自：https://www.bilibili.com/video/BV1Gx411Y7cz/?spm_id_from=333.337.search-card.all.click&vd_source=25d1a12ff92265ad29209fc06224b83d

1.对于0点

首先，百度百科的定义是：泰勒公式是一个用函数在某点的信息描述其附近取值的公式。如果函数满足一定条件，泰勒公式可以用函数在某一点的各阶导数值做系数构建一个多项式来近似表达这个函数。

例如，假设我们想求钟摆实验中某个角度下小球与地面的距离，可以用如下公式计算：

但这里存在的$cos(\theta )$使我们无法直观理解角度和高度的距离，但如果可以用$1-\frac{{\theta }^2}{2}$近似表达cos(θ)，带入后发现结果就很简单了。

从图像上看，这两个函数在0附近十分接近。

这就是我们学习泰勒公式的目的，通过一个多项式（由于多项式函数容易计算、求导、积分），在某点近似一个复杂的函数，以代替该函数研究相关性质。

那么如何构建这个多项式呢（如何选择$c_0$、$c_1$、$c_2$）？这里以cos（x）为例。

首先我们来看$c_0$。当x=0时，cos(0)=1，如果想让所得多项式与cos尽可能相似，我们最好让P(0)同样等于1。带入后就能计算出$c_0$的值为1。

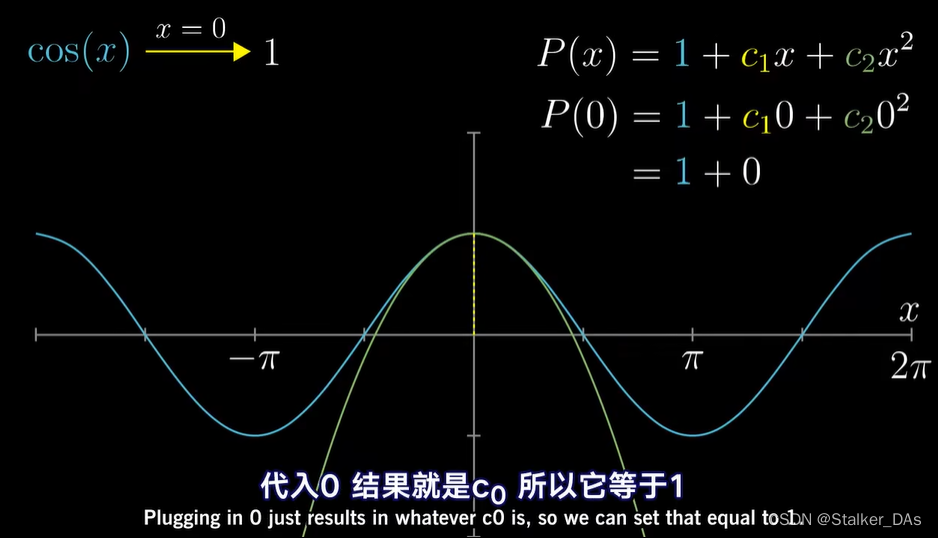
这时无论我们怎么选择$c_1$和$c_2$，x=0时两函数始终有共同的结果1

而在x=0时，如果我们能让函数的切线斜率和cos(x)相等的话就能得到更近似的函数如下图所示，否则近似的多项式函数的值在离x=0处很近的地方就会出现明显的偏差了。

此时，我们计算cos(x)在0处的导数为-sin(0)=0，并带入P(x)中，可以得到$c_1$的结果。也就是常数$c_1$控制着P(x)在x=0处对导数的近似。

而此时我们希望控制函数的凹凸性和函数增减速率（二阶导正负表示开口方向，大小表示斜率）尽可能一致，这时根据上面公式再次求导计算$c_2$

最终可以得到近似函数：$P(x)=1+0x+(-\frac{1}{2})x^2$

经过验证发现结果十分近似

而通过增加多项式的参数，可以使多项式函数与目标函数越来越近似，如下图：

下面将该公式推导至一般形式，首先对于系数$c_i$，想要得到的系数应为想要得到的导数值除以$i!$。

例如cos(x)的四阶导数是1，那么$x^4$的系数应该是1/4!=1/24

2.对于非0点

假设此时我们想在点$\pi$附近进行近似，此时需要使用关于(x-$\pi$)而不是x的多项式来达到相同的效果。

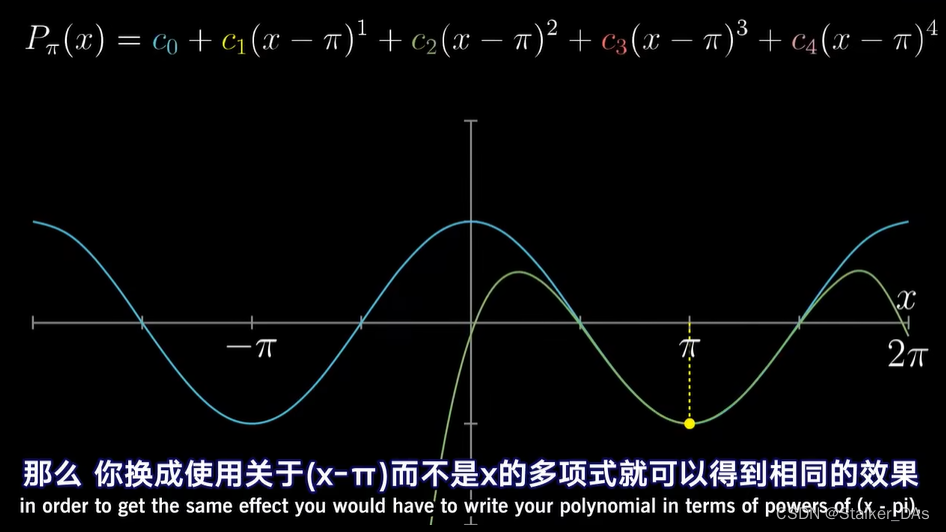
以为此时我们带入x=$\pi$，就可以根据以上方式计算$c_0$、$c_1$等参数。

3.一般性讨论

我们可以认为泰勒公式就是将一点处的导数值信息，转化成这一点附近的函数值信息

而我们通过对cos的讨论发现，可以将P(x)写成一个如下公式，这个公式就是泰勒多项式。

而当我们在处理不规则的函数时，也可以通过求导得到函数P中的每个参数，如上式所示，这就是泰勒多项式的一般形式。

当想要求的非0点的多项式时例如点a，这时就需要用(x-a)改写原多项式：

以上就是泰勒公式的原理和过程。