PnP算法详解

PnP概述
PnP(Perspective-n-Point)是求解3D到2D点的对应方法。它描述了当知道n个3D空间点及其位置，如何估计相机的位姿。如果两张图像中的一张特征点3D位置已知，那么至少需要3个点对(以及至少一个额外验证点验证结果)就可以计算相机的运动。

PnP的应用范围很广比如两阶段法的6D姿态估计以及视觉SLAM等等。

特征点的3D位置可以由三角化或者RGB-D相机的深度图确定，当然还有其他方法。

PnP数学模型
PnP问题的几何结构如下图所示，给定3D点的坐标以及对应2D点的坐标以及内参矩阵，求解相机的姿态。

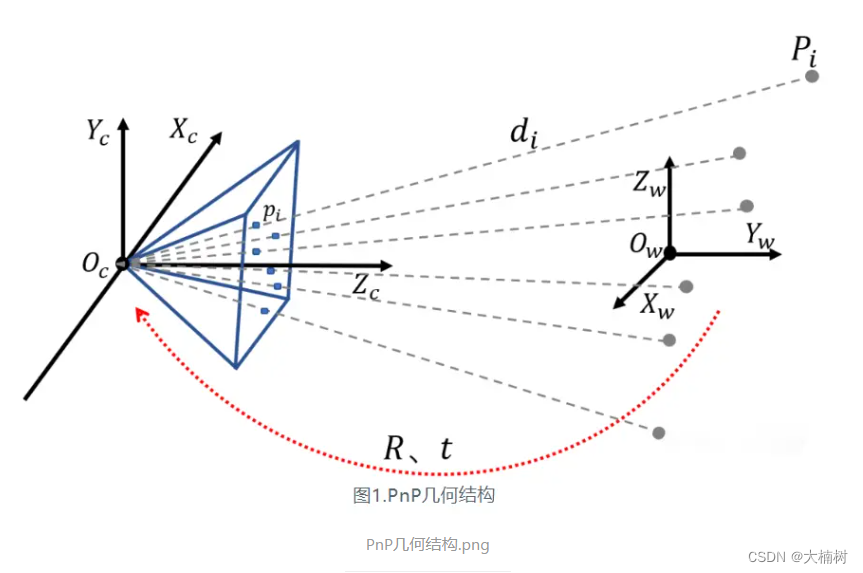
PnP求解方法
DLT直接线性变换
P3P三对点估计位姿
EPnP(Efficient Pnp)
BA(Bundle Adjustment)光速法平差





EPnP




那么为什么在摄像头坐标系中存在同样的加权关系，这里对(2)进行手写推导：



3.计算控制点在相机坐标系下的坐标
手推公式：







在N=4的情况下，有10个未知数，6个方程。在Opencv中实现EPnP算法很简单：

solvePnP(pts_3d, pts_2d, K, Mat(), r, t, CV_EPNP); // 调用OpenCV 的 PnP 求解，可选择EPNP，DLS等方法,默认采用迭代法（最小化重投影）

参考文章
https://zhuanlan.zhihu.com/p/361791835
https://blog.csdn.net/jessecw79/article/details/82945918#control_points_64
[泡泡机器人公开课]第三十九课：PnP 算法简介&代码解析-柴政