基于机器人的齐次变换矩阵及其运算

一 齐次变换矩阵及其运算

由于各种原因，变换矩阵应该写成方型形式，33或者44即可。

为保证所表示的矩阵为方阵，如果在同一矩阵中既表示姿态又表示位置，那么在矩阵中加入比例因子使之成为4*4的矩阵即可。

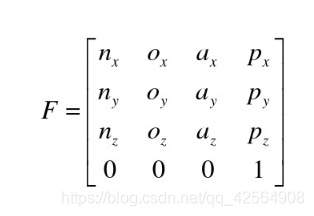
变换可以定义为空间的一个运动。

已知一直角坐标系中某点坐标，那么该点在另一直角坐标系中的坐标可通过齐次坐标变换来求得。

变换可分为如下形式：

纯平移

纯旋转

平移和旋转的结合

1.平移的齐次变换

空间的某一点在直角坐标系中的平移，由A（X,Y,Z）平移至A’(X’,Y’,Z’)，即

其中

@1算子左乘：表示点的平移是相对固定坐标系进行的坐标转换。

@2算子右乘：表示点的平移是相对动坐标系进行的坐标转换。

@3该公式亦适用于坐标系的平移转换，物体的平移转换，如机器人手部的平移转换。

具体解题步骤如下（A’）：
（因为是A相对于固定坐标系做平移，所以是左乘）

因为是A相对于动坐标系做平移，所以是左乘

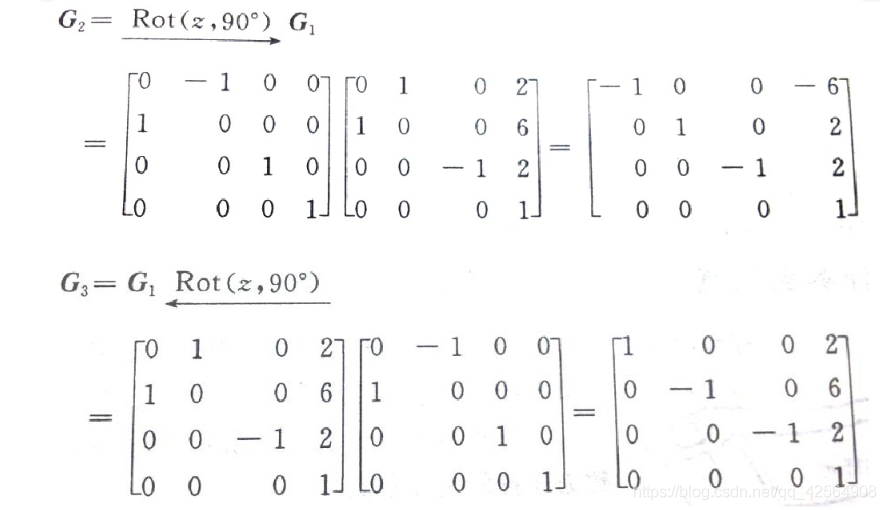
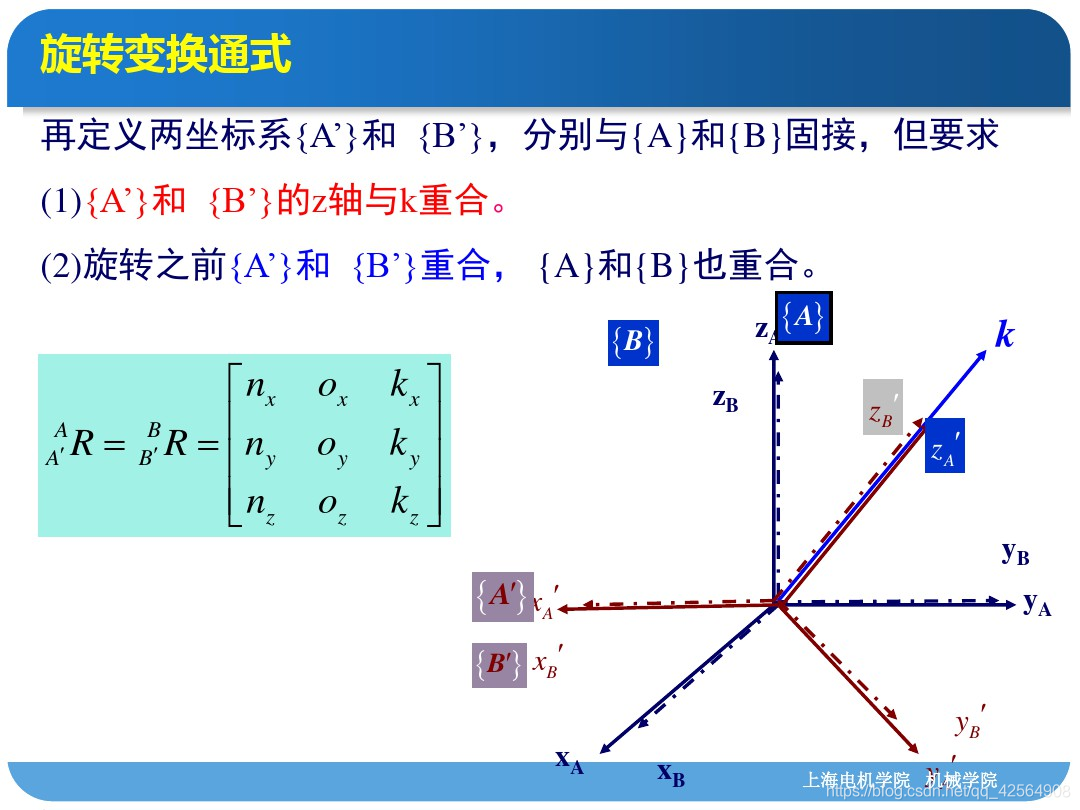
2.旋转的齐次变换

点在空间直角坐标系中的旋转如图所示，A（X,Y,Z）绕Z轴旋转sita角后至A’(X’,Y’,Z’)，则A与A‘之间的关系为：