引力势的球谐展开（从泰勒级数到勒让德多项式）

Sparse Direction

已于 2024-04-27 18:38:35 修改

阅读量422

点赞数 5

文章标签：几何学

于 2024-04-27 12:45:07 首次发布

本文链接：https://blog.csdn.net/qq_42691741/article/details/138245341

版权

1.从泰勒展开到勒让德再到球谐函数

小质元对引力势引起的作用

1.1引力位的泰勒级数表达

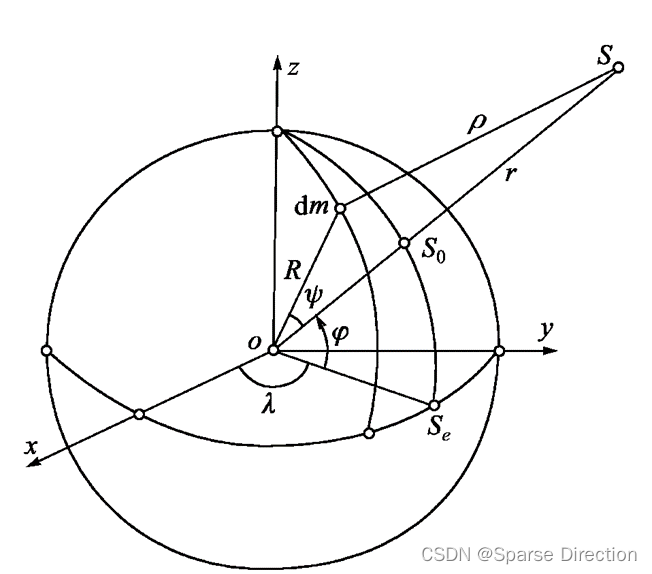
引力位表达式为
$\int _ { M } \frac { 1 } { \rho } d m$
其中
$\rho ^ { 2 } = r ^ { 2 } + R ^ { 2 } - 2 R r \cos \psi = r ^ { 2 } ( 1 + ( \frac { R } { r } ) ^ { 2 } - 2 \frac { R } { r } \cos \psi )$
令
$\frac { R } { r } ) ^ { 2 } - 2 \frac { R } { r } \cos \psi$
则原来的距离倒数为
$\frac { 1 } { \rho } = \frac { 1 } { r } ( 1 + l ) ^ { - \frac { 1 } { 2 } }$
对其进行泰勒展开
$\frac { f ( x _ { 0 } ) } { 0 ! } + \frac { f ^ { \prime } ( x _ { 0 } ) } { 1 ! } ( x - x _ { 0 } ) + \frac { f ^ { \prime \prime } ( x _ { 0 } ) } { 2 ! } ( x - x _ { 0 } ) ^ { 2 } + \cdots +\frac { f ^ { ( n ) } ( x _ { 0 } ) } { n ! } ( x - x _ { 0 } ) ^ { n }+R_n(x)$
将 $\frac{1}{\rho}$ 在 $l = 0$ 处展开得到
$\frac { 1 } { \rho } = \frac { 1 } { r } ( 1 + l ) ^ { - \frac { 1 } { 2 } } = \frac { 1 } { r } ( 1 - \frac { 1 } { 2 } l + \frac { 3 } { 8 } l ^ { 2 } - \frac { 5 } { 1 6 } l ^ { 3 } + \cdots )$
引力位级数表达为
$\frac { G } { r } \int ( 1 - \frac { 1 } { 2 } l + \frac { 3 } { 8 } l ^ { 2 } - \frac { 5 } { 1 6 } l ^ { 3 } + \cdots ) d m$
将 $l$ 表达式代入得
$\frac { G } { r } \int ( 1 - \frac { 1 } { 2 } \left[ ( \frac { R } { r } ) ^ { 2 } - 2 \frac { R } { r } \cos \psi \right] + \frac { 3 } { 8 } \left[ ( \frac { R } { r } ) ^ { 2 } - 2 \frac { R } { r } \cos \psi \right] ^ { 2 }- \frac { 5 } { 1 6 } \left[ ( \frac { R } { r } ) ^ { 2 } - 2 \frac { R } { r } \cos \psi \right] ^ { 3 } + \cdots ) d m$

1.2 泰勒级数到勒让德多项式

按照 $\frac{R}{r}$ 整理得
$\cdots = \sum _ { i = 0 } ^ { n } v _ { i }$
其中
$\frac { G } { r } \int _ { M } d m$
$\frac { G } { r } \int _ { M } \frac { R } { r } \cos \psi d m$
$\frac { G } { r } \int _ { M } ( \frac { R } { r } ) ^ { 2 } ( \frac { 3 } { 2 } \cos ^ { 2 } \psi - \frac { 1 } { 2 } ) d m$
当然，零阶项、一阶项、二阶项等的表达都有其实际的物理意义，此处暂不作展开。进行代换有
$\cos \psi ) = 1$
$\cos \psi ) = \cos \psi$
$\cos \psi ) = \frac { 3 } { 2 } \cos ^ { 2 } \psi - \frac { 1 } { 2 }$
于是就有（类似）勒让德表达。直接给出 $\cos \psi )$ 一般表达式
$\cos \psi ) = \frac { 1 } { 2 ^ { n } n ! } \frac { d ^ { n } ( \cos ^ { 2 } \psi - 1 ) ^ { n } } { d ( \cos \psi ) ^ { n } }$
当已知一阶项和二阶项时，有递推式
$\frac { 2 n + 1 } { n + 1 } x P _ { n } ( x ) - \frac { n } { n + 1 } P _ { n - 1 } ( x ),x = \cos \psi$
于是，用勒让德公式表示第 $\bm n$ 阶地球引力位公式为
$\frac { G } { r } \int ( \frac { R } { r } ) ^ { n } P _ { n } ( \cos \psi ) d m$

1.3 勒让德多项式到缔合勒让德和球谐函数

由于 $\psi$ 角余弦是M点和S点的直角坐标的函数。也可以用球面三角学公式表示为两点的球面坐标函数，经过变换之后，即可得到 $n$ 阶重力位的计算公式
$\frac { 1 } { r ^ { n + 1 } } \left[ A _ { n } P _ { n } ( \cos \theta ) + \sum _ { K = 1 } ^ { n } ( A _ { n } ^ { K } \cos K \lambda + B _ { n } ^ { K } \sin K \lambda ) P _ { n } ^ { K } ( \cos \theta ) \right]$
其中， $\theta$ 为极距， $\phi+\theta=90\degree$ ， $P_n(\cos\theta)$ 称为带球函数， $P_n^K(\cos\theta)$ 称为缔合勒让德函数。
$\sum _ { n = 0 } ^ { \infty } V _ { n } = \sum _ { n = 0 } ^ { \infty } \frac { 1 } { r ^ { n + 1 } } \left[ A _ { n } P _ { n } ( \cos \theta ) + \sum _ { K = 1 } ^ { n } ( A _ { n } ^ { K } \cos K \lambda + B _ { n } ^ { K } \sin K \lambda ) P _ { n } ^ { K } ( \cos \theta ) \right]$
其中， $\cos K\lambda P_n^K(\cos\theta)$ 和 $\sin K\lambda P_n^K(\cos\theta)$ 称为缔合球函数。
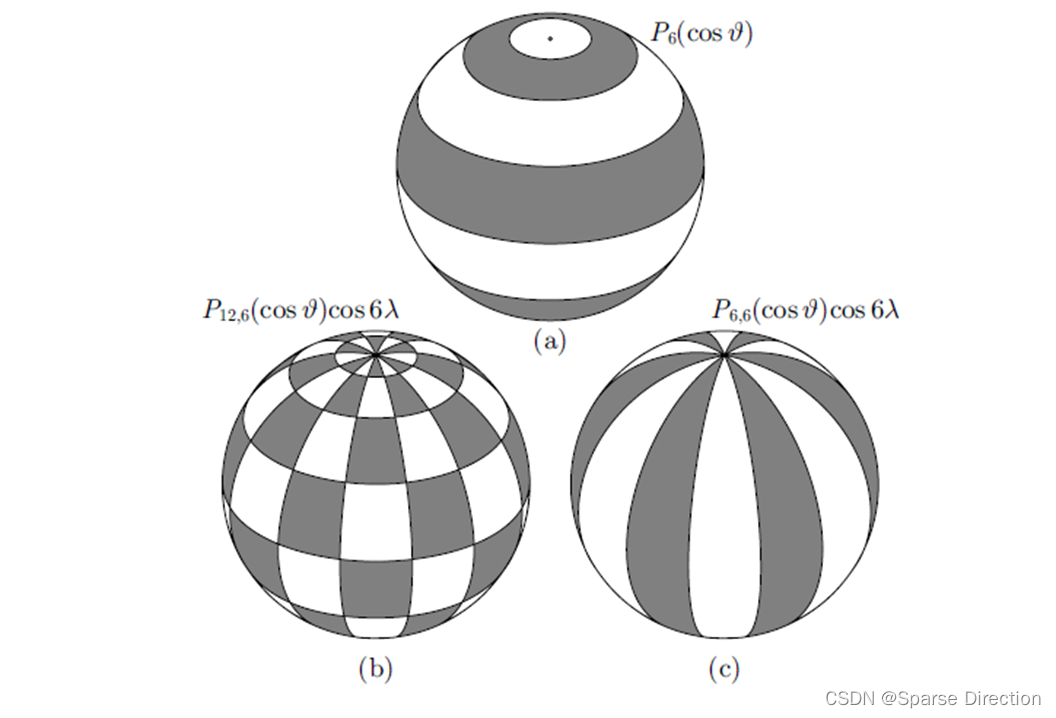
$K = n$ 时称扇球函数， $\neq n$ 时称田球函数
带谐、扇谐和田谐

2.低阶项的物理意义

2.1零阶项

$\frac { G } { r } \int _ { M } d m = \frac { G M } { r }$
解释和应用： $v_0$ 就是把地球质量集中到地球质心处时的点的位。也就是说，将地球看作为一个质点时，与其距离为𝑟点处的引力位为 $v_0$ 。

2.2一阶项

$\cos \psi = \frac { \bm R \cdot \bm r } { R r } = \frac { x x _ { m } + y y _ { m } + z z _ { m } } { R r }$
$\frac { G } { r } \int _ { M } \frac { R } { r } \cos \psi d m = \frac { G } { r } \int _ { M } ^ { }\frac{R}{r} \frac { x x _ { m } + y y _ { m } + z z _ { m } } { R r } d m = \frac { G } { r ^ { 3 } } \int _ { M } ( x x _ { m } + y y _ { m } + z z _ { m } ) d m$
$\frac { G } { r ^ { 3 } } ( \int _ { M } ^ { } x x _ { m } d m + \int _ { M } ^ { } y y _ { m } d m + \int _ { M } ^ { } z z _ { m } d m )$
物质质心坐标定义为
$\frac { \int _ { M } ^ {} x _ { m } d m } { M } , y _ { 0 } = \frac { \int _ { M } ^ {} y _ { m } d m } { M } , z _ { 0 } = \frac { \int _ { M } ^ {} z _ { m } d m } { M }$
因为坐标原点置于地球的质心，所以
$v _ { 1 } = 0$
解释和应用： 卫星的三维位置 $(x, y, z)$ 是在地心坐标系下给出的。若卫星反演出的地球重力场的一阶项 $\neq 0$ ，那么，则意味着所用的三维坐标系的原点不在地球质量中心，坐标系的原点需要重新进行标定。卫星在大气层外飞行，所以根据其确定的地球质心位置，是包含整个大气、海洋在内的地心位置。

2.3二阶项

$\frac { G } { r } \int _ { M } ( \frac { R } { r } ) ^ { 2 } ( \frac { 3 } { 2 } \cos ^ { 2 } \psi - \frac { 1 } { 2 } ) d m$
$R ^ { 2 } = x _ { m } ^ { 2 } + y _ { m } ^ { 2 } + z _ { m } ^ { 2 }$
$\cos \psi = \frac { \bm R \cdot \bm r } { R r } = \frac { x x _ { m } + y y _ { m } + z z _ { m } } { R r }$
替换可得
$\frac { G } { r } \int _ { M } ( \frac { R } { r } ) ^ { 2 } ( \frac { 3 } { 2 } ( \frac { x x _ { m } + y y _ { m } + z z _ { m } } { R r } ) ^ { 2 } - \frac { 1 } { 2 } ) d m$
$\frac { f } { 2 r ^ { 5 } } \left[ ( y ^ { 2 } + z ^ { 2 } - 2 x ^ { 2 } ) A + ( x ^ { 2 } + z ^ { 2 } - 2 y ^ { 2 } ) B +( x ^ { 2 } + y ^ { 2 } - 2 z ^ { 2 } ) C + 6 y z D + 6 x z E + 6 x y F \right]$

其中相关的符号说明：质点M对坐标轴的转动惯量
$\int _ { M } ( y _ { m } ^ { 2 } + z _ { m } ^ { 2 } ) d m \quad B= \int _ { M } ( x _ { m } ^ { 2 } + z _ { m } ^ { 2 } ) d m \quad C = \int _ { M } ( x _ { m } ^ { 2 } + y _ { m } ^ { 2 } ) d m$
离心力矩
$\int _ { M } ( y _ { m } z _ { m } ) d m \quad E = \int_ { M } ( x _ { m } z _ { m } ) d m \quad F = \int_ { M } ( x _ { m } y _ { m } ) d m$
化成球坐标系，S的极坐标系为
$\begin{matrix} x = r . \cos \varphi \cos \lambda \\ y = r . \cos \varphi \sin \lambda \\ z = r . \sin \varphi \end{matrix}$
于是
$v_2= \frac { G } { r ^ { 3 } } \left[ \frac { 2 C - A - B } { 2 } ( \frac { 1 } { 2 } - \frac { 3 } { 2 } \sin ^ { 2 } \varphi ) + 3 ( E \cos \lambda + D \sin \lambda ) \cos \varphi \sin \varphi + \frac { 3 } { 2 } ( \frac { B - A } { 2 } \cos 2 \lambda + F \sin 2 \lambda ) \cos ^ { 2 } \varphi \right]$
$v_2= \frac { G } { r ^ { 3 } } \left[ \frac { 2 C - A - B } { 2 } ( \frac { 1 } { 2 } - \frac { 3 } { 2 } \sin ^ { 2 } \varphi ) + \frac { 3 } { 2 } ( \frac { B - A } { 2 } \cos 2 \lambda \cos ^ { 2 } \varphi ) + 3 ( E \cos \lambda + D \sin \lambda ) \cos \varphi \sin \varphi + \frac { 3 } { 2 } F \sin 2 \lambda \cos ^ { 2 } \varphi \right]$
解释和应用： 引力位的二阶球谐系数与地球的扁率和极潮变化直接相关

Sparse Direction

关注

5
点赞
踩
6

收藏

觉得还不错? 一键收藏
1
评论
引力势的球谐展开（从泰勒级数到勒让德多项式）

1.从泰勒展开到勒让德再到球谐函数1.1引力位的泰勒级数表达引力位表达式为V=G∫M1ρdmV = G \int _ { M } \frac { 1 } { \rho } d mV=G∫Mρ1dm其中ρ2=r2+R2−2Rrcos⁡ψ=r2(1+(Rr)2−2Rrcos⁡ψ) \rho ^ { 2 } = r ^ { 2 } + R ^ { 2 } - 2 R r \cos \psi = r ^ { 2 } ( 1 + ( \frac { R } { r } ) ^ { 2 } - 2 \
复制链接

扫一扫