医图论文 Arxiv‘24 | MambaEviScrib：Mamba和证据引导的一致性使CNN在涂鸦基础的弱监督超声图像分割中稳健工作

论文信息

题目：MambaEviScrib: Mamba and Evidence-Guided Consistency Make CNN Work Robustly for Scribble-Based Weakly Supervised Ultrasound Image Segmentation

MambaEviScrib：Mamba和证据引导的一致性使CNN在涂鸦基础的弱监督超声图像分割中稳健工作

作者：Xiaoxiang Han, Xinyu Li, Jiang Shang, Yiman Liu, Keyan Chen, Qiaohong Liu, Qi Zhang

源码：https://github.com/GtLinyer/MambaEviScrib

论文创新点

1. 双分支涂鸦基础的弱监督分割框架：作者提出了一个包含CNN和Mamba的双分支网络框架，这一框架能够分别提取超声图像中的局部解剖细节和全局形态特征。这种结构的设计使得模型在处理局部特征的同时，也能够捕获图像的全局信息，提高了分割的准确性。
2. 证据引导的一致性（EGC）策略：作者引入了基于Dempster-Shafer理论的证据引导的一致性策略，该策略利用高证据预测来指导低证据预测的优化。这一策略特别针对超声图像中边缘区域的分割稳定性进行了增强，提高了模型对于边缘区域预测的鲁棒性。
3. 损失函数的协同优化：作者提出了一种新的损失函数，该函数结合了证据损失和门控条件随机场（CRF）损失，通过利用输入图像的特征和真值，共同优化两个分支中的伪标签生成。这种方法进一步提升了模型在边缘分割任务中的表现。

摘要

从超声图像中分割解剖结构和病变有助于疾病评估、诊断和治疗。基于稀疏注释的弱监督学习（WSL）已取得鼓舞人心的性能，并展示了减少注释成本的潜力。然而，超声图像常受到对比度差、边缘不清晰以及病变大小和位置不一等问题的困扰。这使得具有局部接受场的卷积网络难以从涂鸦注释提供的稀疏信息中提取全局形态特征。最近，基于状态空间序列模型（SSMs）的视觉Mamba在确保长期依赖性的同时显著降低了计算复杂性，与Transformers相比。因此，我们首次将涂鸦基础的WSL应用于超声图像分割，并提出了一种新颖的混合CNN-Mamba框架。此外，由于超声图像的特性和不足的监督信号，现有的一致性正则化经常过滤掉接近决策边界的预测，导致边缘的不稳定预测。因此，我们引入了Dempster-Shafer理论（DST）来设计一种证据引导的一致性（EGC）策略，该策略利用更有可能出现在高密度区域附近的高证据预测来指导可能位于决策边界附近的低证据预测进行优化。在训练期间，所提出的框架中的CNN分支和Mamba分支基于EGC策略相互启发。在四个超声公共数据集上的大量实验表明了所提方法的竞争力。

关键词

弱监督学习，Mamba，证据深度学习，图像分割，超声

1. 引言

医用超声成像在医学诊断领域占有举足轻重的地位，因为它具有多种优点，包括无放射性损伤、高实时性能、出色的动态显示能力以及方便和成本效益。它可以安全地应用于对辐射敏感的人群，如孕妇和儿童，并且还可以实时显示器官和组织的细节结构和动态变化，为临床医生提供直观的病理条件评估。此外，超声成像的操作简便和经济实惠促成了其在临床实践中的广泛应用，使其成为许多疾病的首选或必需的检查方法。[1]。从超声图像中分割解剖结构和病变在临床实践中起着重要作用。它可以为临床医生提供有价值的参考信息，如器官或病变的形态、大小、位置以及与周围组织的关系。随后，这些信息帮助临床医生进行早期疾病诊断、病情评估和治疗计划。[2]。随着深度学习（DL）[3, 4, 5]的进步，在医学图像分割方面取得了显著进展。通常，用于分割的监督学习方法需要大规模像素级注释数据来有效训练准确的模型。然而，医学超声图像的注释与自然图像不同，需要专业的医学专业知识。因此，大规模超声图像的像素级注释既昂贵又耗时。为了解决这一挑战，研究人员致力于开发不依赖精确密集注释的深度学习技术，如弱监督学习（WSL）[8, 9, 10]、半监督学习[11]和自监督学习[12, 5]。本研究专注于探索基于涂鸦注释的WSL方法。该方法采用的稀疏注释比密集注释更容易获得，并且比其他稀疏注释方法更便捷、多功能和适应性强[13]。

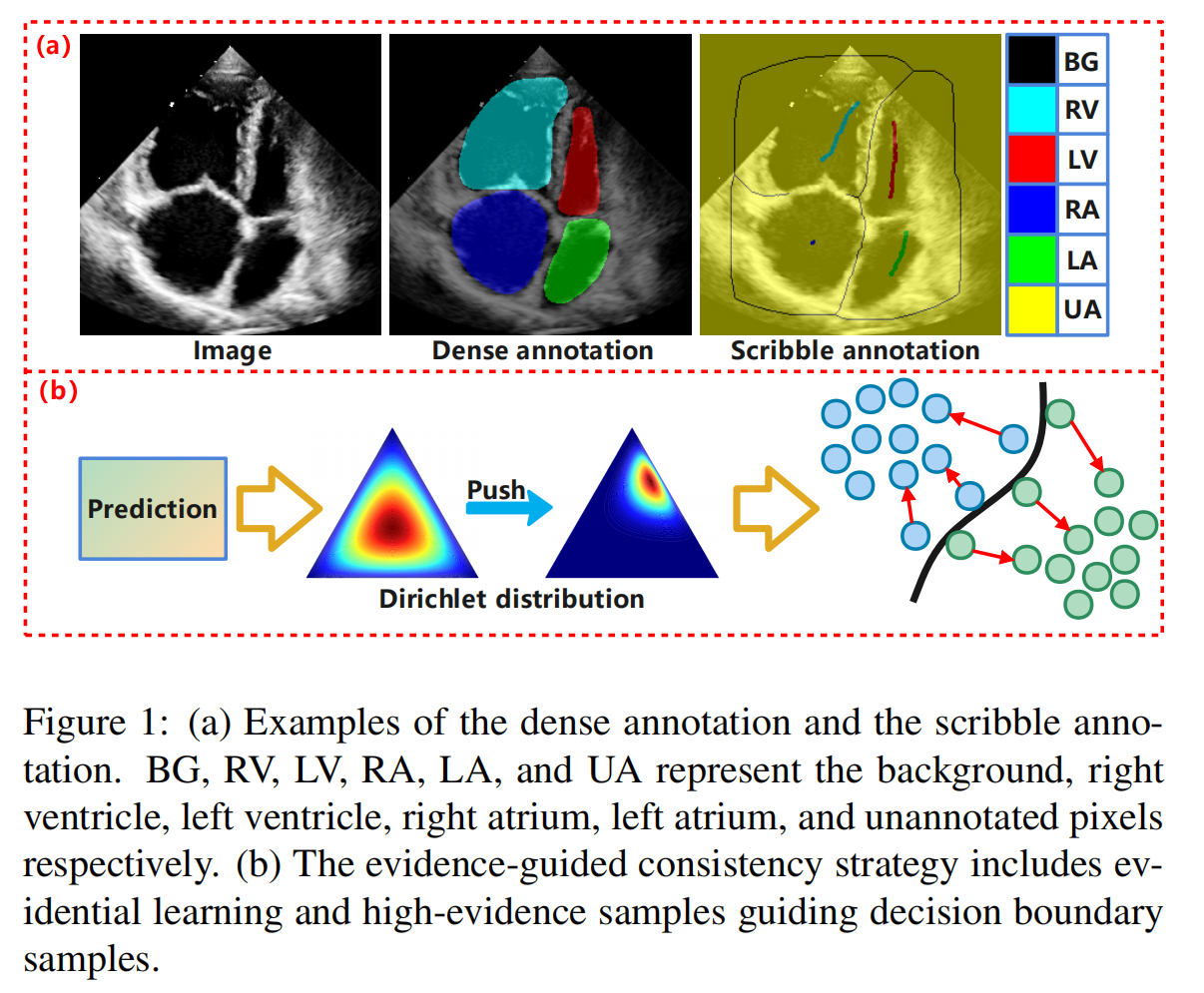
如图1(a)所示，通过提供涂鸦形式的掩码，仅注释一小部分像素，这种方法可以有效降低注释成本并提高注释效率。鉴于涂鸦代表感兴趣区域的一小部分，基于涂鸦注释的弱监督分割的主要挑战来自于训练监督信息的不足。为了有效利用未注释像素的信息，提出了许多方法。例如，一些方法使用生成器和鉴别器[14, 15]来学习特征，但它们需要额外的密集注释，从而增加了成本。一些方法设计了正则化损失函数，如归一化切割损失[16]和条件随机场损失[17]。一些方法引入了辅助任务，利用分割的替代表示，如距离图[18]或边缘图[19]。其他方法设计了一致性正则化策略[20, 21]，以鼓励网络对同一输入在各种扰动下产生一致的输出。然而，基于CNN的方法由于局部接受场的限制而难以捕获全局信息。然而，超声图像中病变的大小和位置不一的挑战需要模型感知全局特征。尽管Transformer及其变体在捕获长期依赖性方面表现出优越性，但其二次复杂度O(n^2)导致了高计算成本。最近，Mamba[22]因其独特的线性时间复杂度O(N)、低内存占用和有效处理长序列而受到广泛关注。通过有效地平衡计算复杂性和长期依赖性，Mamba显示出显著的性能，有望取代Transformers。此外，尽管一些方法[23]试图减少分割不确定性，但它们倾向于丢弃低置信度像素。然而，超声图像常表现出对比度差和斑点噪声，导致病变或解剖边界周围的边缘特征模糊且不明确。在这种情况下，忽略决策边界附近的低置信度预测可能导致信息丢失，最终干扰分割的准确性。为此，我们提出了一种新颖的基于涂鸦的弱监督模型，用于超声图像分割，称为MambaEviScrib，包括双分支网络，即混合CNN和Mamba分支，以及证据引导的一致性（EGC）策略。具体来说，CNN分支和Mamba分支分别提取局部特征和全局表示，使作者能够捕获超声图像中的局部解剖细节和全局形态特征。随后，Dirichlet分布被用来参数化分割概率的概率分布，即第二阶概率，并估计不确定性。这是通过利用更有可能出现在高密度区域附近的高证据预测来指导可能位于决策边界附近的低证据预测的优化过程。我们称这个过程为EGC策略，其概念在图1(b)中简单地显示。这种方法增强了模型的鲁棒性和可信度，同时也提高了边缘分割的稳定性。

此外，我们将证据损失函数与门控条件随机场（CRF）损失函数[17]结合起来。通过利用输入图像的特征和真值，我们共同优化两个分支中的伪标签生成。这种方法使模型能够利用输入图像的监督信息和形态信息更好地处理边缘。我们在四个超声公共数据集上进行了广泛的实验：CardiacUDA[26]、EchoNet[27]、BUSI[28]和DDTI[29]。注意，作者的方法仅在推理阶段使用U-Net，并且我们没有对U-Net进行任何修改。因此，与其他复杂模型相比，我们享有优越的推理效率。本文的主要贡献如下。

1. 作者提出了一个双分支涂鸦基础的弱监督分割框架，包括CNN和Mamba，分别从超声图像中提取局部解剖细节和全局形态特征。
2. 引入了证据引导的一致性（EGC）策略，充分利用决策边界附近的预测，增强边缘分割的稳定性和模型的鲁棒性。
3. 引入的损失函数共同优化了使用输入图像特征和真值生成的伪标签，进一步提高了边缘分割性能。
4. 据我们所知，我们是第一个将涂鸦基础的WSL应用于超声图像分割的。我们将公开发布四个超声数据集及其涂鸦注释，以及我们的代码。

3. 方法

我们定义B模式超声扫描的2D灰度图像为$X\in RW\times H$，其中$W$和$H$分别代表图像的宽度和高度。弱监督分割的目标是识别$X$中每个像素$k\in X$所属的类别，从而形成语义标签图 Y ^ ∈ { 0 , 1 , … , K } W × H \hat{Y} \in \{0, 1, \ldots, K\}W \times H Y^∈{0,1,…,K}W×H，其中$K=0$代表背景类别，$K>0$表示目标类别。我们使用包含$N$个样本的数据集$D=\{(X,Y_i){\}}_{i=1}^N$进行训练，其中$X_i$代表输入图像，$Y_i$表示涂鸦注释。在多类别分割的背景下，$Y_i$包含$K+1$个类别的标签：0表示未标记像素，$1\sim K-1$代表目标病变像素，$K$表示背景像素。我们的框架包括一个U-Net和一个MambaUNet，训练前随机初始化它们的参数。在将图像输入模型之前，它们会经过包括旋转、翻转和颜色抖动在内的变换。两个网络的输出将通过EGC策略进行优化。此外，证据损失函数和门控CRF损失函数被用来优化伪标签的生成。详细信息将在后续详细说明。所提出的流程在图2中进行了说明。

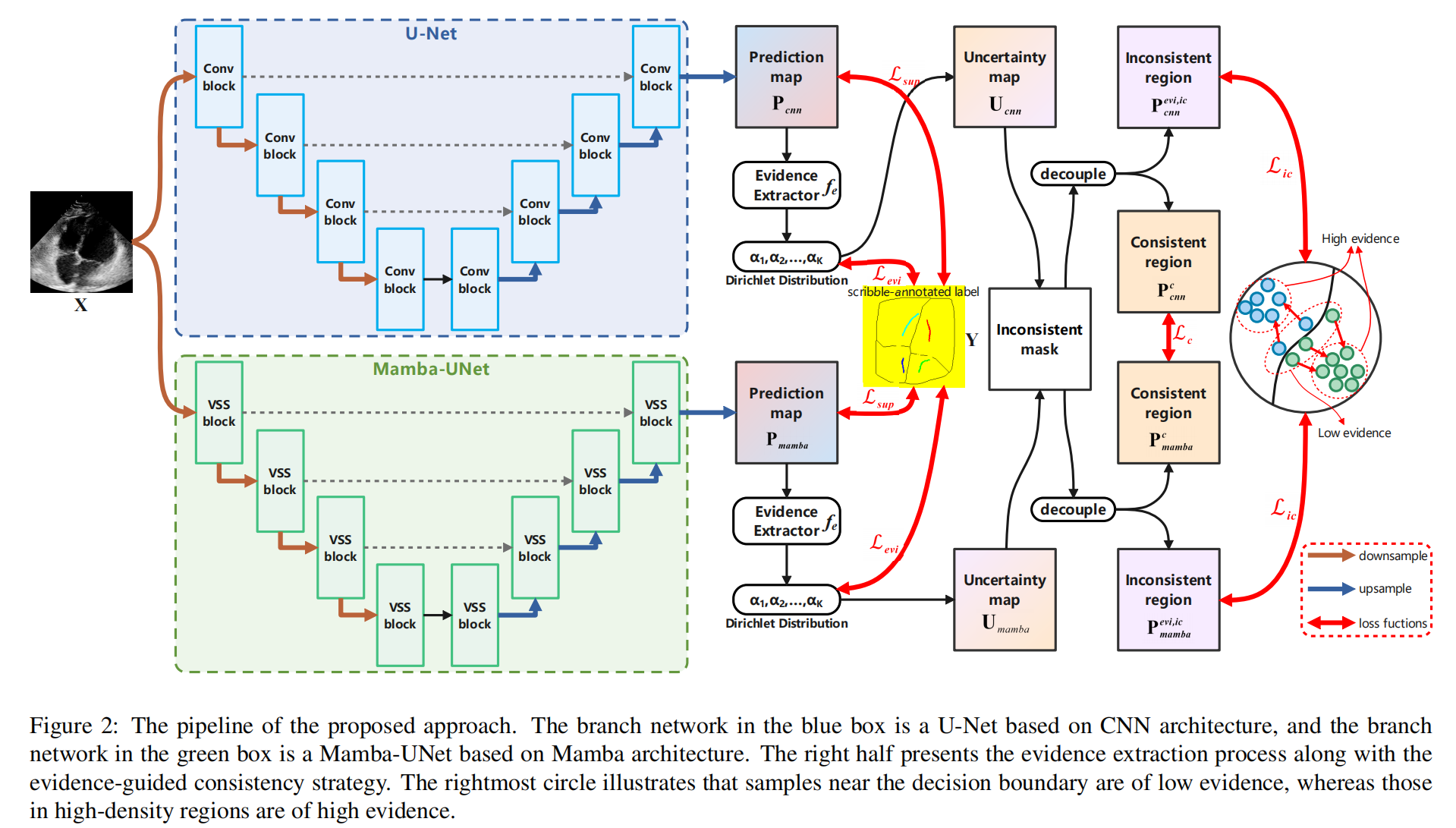
3.1. CNN-Mamba双分支网络

两个网络分支，U-Net和Mamba-UNet，分别表示为$F_{cnn}(\cdot ;{\Theta }_{cnn})$和$F_{mamba}(\cdot ;{\Theta }_{mamba})$，在图2中以蓝色和绿色突出显示。输入图像$X$被分别输入到两个网络中以获得预测$P_{cnn},P_{mamba}\in R^{K\times W\times H}$。整个过程简洁地表达为：
$$P_{cnn}=F_{cnn}(X;{\Theta }_{cnn})$$
$$P_{mamba}=F_{mamba}(X;{\Theta }_{mamba})$$
其中${\Theta }_{cnn}$和${\Theta }_{mamba}$分别代表网络的可学习参数。UNet[6]，作为一种经典的医学图像分割网络，已经被研究了很长时间，提供了良好的性能和计算效率。然而，基于CNN的UNet缺乏捕获全局信息的能力，这在Mamba-UNet[53]的指导下得到了增强。Mamba-UNet基于Mamba，它既能够捕获全局信息，又具有线性复杂度。

3.1.1. CNN分支

由于UNet被广泛认可，我们只给出一个简短的介绍。U-Net架构，形状像字母’U’，包括一个编码器和一个解码器。编码器由多个卷积块和池化层组成，用于下采样，每个卷积块通常包括$3\times 3$卷积、批量归一化和ReLU或LeakyReLU激活函数。解码器反过来由类似的卷积块以及转置卷积层组成，用于上采样。此外，解码器的每个层都通过跳跃连接与其对应的编码器层相连。

3.1.2. Mamba分支

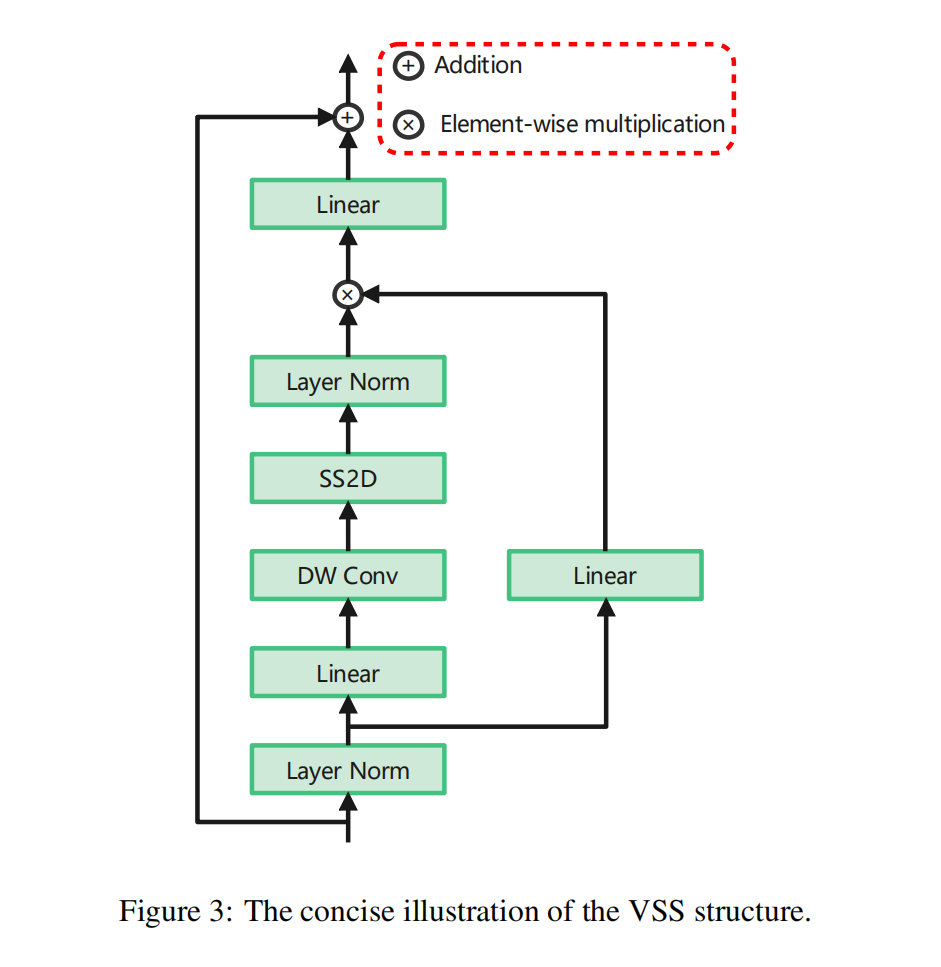
随着状态空间模型（SSM）和结构化SSM（S4）[54]的引入和发展，它们在处理长序列方面的高效性能有望成为高成本Transformers的经济有效的替代品。传统的SSM作为线性时不变系统的函数，由状态方程和观测方程组成，它们被表述为线性常微分方程（ODE）。状态方程描述了系统状态变量随时间的演变。它通常包括当前状态、输入和可能的系统参数。数学上，状态方程可以表示为：
$$h^{\prime }(t)=Ah(t)+Bx(t)$$
其中$h(t)\in RN$代表时间步$t$时的系统状态，$h^{\prime }(t)$表示状态向量$h(t)$关于时间$t$的导数，$x(t)\in R$是时间步$t$的输入，$A\in RN\times N$是状态转移矩阵，$B\in RN$是输入控制矩阵。观测方程描述了系统输出与其状态之间的关系，可以数学表达为：
$$y(t)=Ch(t)+Dx(t)$$
其中$y(t)\in R$代表时间步$t$的系统输出，$C\in RN$是输出矩阵，$D\in R^1$是直接馈通矩阵，它描述了输入信号如何直接影响输出。通过引入时间尺度参数$\Delta$，参数$A$和$B$可以使用零阶保持（ZOH）方法进行离散化，定义如下：
$$A=e^{\Delta A},B=(\Delta A{)}^{-1}\left(e^{\Delta A}-I\right)\cdot \Delta B$$
SSMs的离散化公式如下：
$$h^{\prime }(t)=Ah(t)+Bx(t)$$
$$y(t)=Ch(t)+Dx(t)$$
S4是SSM的离散化版本，引入了高振荡偏微分方程（HIPPO）矩阵来解决长期依赖性问题，同时使用低秩分解来降低计算复杂性。它采用卷积架构来表示离散化的SSM，可以表述如下：
$$K=\left[CB,CAB,\dots ,C{A}^{L-1}B\right]$$
$$y=x\ast K$$
其中$K\in RL$代表结构化卷积核，$L$代表输入序列$x$的长度。Mamba[22]继承了S4的优势，结合了选择性机制，并经过硬件优化，从而在处理复杂任务方面提高了性能。VMamba[55]提出了视觉状态空间（VSS）块，利用2D选择性扫描（SS2D）将Mamba技术引入计算机视觉领域，如图3所示。这种方法使空间域的遍历成为可能，并将非因果视觉图像转换为有序的补丁序列，然后由SSM处理每个特征序列。随后，VSS已成为众多视觉Mamba的核心模块。在本研究中，我们采用了Mamba-UNet[53]，它类似于U-Net架构，作为Mamba分支网络。网络输入的2D灰度图像首先通过一个投影层处理以获得1-D序列的不重叠补丁嵌入。输入尺寸$H\times W\times 1$被下采样并调整通道至$H/4\times W/4\times C$。随后，补丁令牌通过VSS块进行特征提取，然后通过补丁合并层进行下采样和维度扩展。编码器中的特征图经过多级处理，输出尺寸分别为KaTeX parse error: Undefined control sequence: \timesC at position 16: H/4 \times W/4 \̲t̲i̲m̲e̲s̲C̲，$H/8\times W/8\times 2C$，$H/16\times W/16\times 4C$和$H/32\times W/32\times 8C$。解码器包括VSS块以及为上采样和维度降低而设计的补丁扩展层。此外，跳跃连接被用来增强下采样过程中丢失的空间细节。

3.2. 证据引导的一致性策略

3.2.1. 证据和不确定性建模

为了建模证据和不确定性，我们引入了EDL。在EDL中，每个像素被分配信念质量和不确定性质量。我们首先使用一个转换函数$f_e(\cdot )$来得出对应于第$i$个像素（ i ∈ { 0 , 1 , … , W × H } i \in \{0, 1, \ldots, W \times H\} i∈{0,1,…,W×H}）的证据向量$e_i$。这确保了证据向量保持非负。过程如下：
$$e_i=f_e(P_i)=\tanh \left(\frac{P_i}{\tau }\right)$$
其中$P_i$代表CNN或Mamba分支网络输出的第$i$个像素，$\tau$表示缩放因子。对于具有$K$个互斥类别（包括背景类别）的分割任务，我们有$e_i=\left[e_{1i},e_{2i},\dots ,e_{Ki}\right]$。参数为${\alpha }_i$的Dirichlet分布被公式化为：
$${\alpha }_{ki}=e_{ki}+1$$
其中$k=1,2,\dots ,K$代表第$k$个类别。Dirichlet强度$S_i$被定义为：
$$S_i=\sum _{k=1}^K{\alpha }_{ki}$$
信念质量$b_{ki}$和总体不确定性质量$u_i$被公式化为：
$$b_{ki}=\frac{e_{ki}}{S_i},u_i=\frac{K}{S_i}$$
其中$b_{ki}\ge 0$, $u_i\ge 0$。这些质量值总和为一，即：
$$u_i+\sum _{k=1}^K{b}_{ki}=1$$
这意味着不确定性与证据的总量成反比。如果没有证据（即${\sum }_k{e}_{ki}=0$），每个类别的信念为零，不确定性为一。反之，如果总证据足够大，不确定性$u_i$将很小，这意味着模型对其预测有很高的信心。第$i$个像素的预测概率分布被公式化为：
$$p_{ki}=\frac{{\alpha }_{ki}}{S_i}$$
因此，预测概率的Dirichlet分布密度函数被公式化为：
$$D(p_i|{\alpha }_i)=\frac{1}{B({\alpha }_i)}\prod _{k=1}^K{p}_{ki}^{{\alpha }_{ki}-1}$$
其中$B({\alpha }_i)$表示$K$维多项式Beta函数，$S^K$代表$K$维单位单纯形：
$$S^K=\left\{p|\sum _{i=1}^K{p}_i=1\text{ and }0\le p_1,\dots ,p_K\le 1\right\}$$

3.2.2. 证据引导的一致性

首先，我们需要分离两个网络分支预测的不一致部分。鉴于预测信心和伪标签质量在训练过程中不断演变，需要一个动态阈值来确定不一致区域。在训练的初始阶段，应保持阈值尽可能低，以促进伪标签的多样化。阈值表达如下：
$${\lambda }_{iter}=\eta \frac{1}{B}\sum _{b=1}^B{f}_{max}(1-U)+(1-\eta ){\lambda }_{iter-1}$$
其中$iter$代表当前迭代索引，$\eta$是随着训练迭代增加而增加的权重，$B$表示批次大小，$f_{max}(\cdot )$表示获取最大值，$U\in RW\times H$是归一化不确定性图。阈值${\lambda }_{cnniter}$和${\lambda }_{mambaiter}$分别定义为Ucnn和Umamba。为了促进伪标签的多样性，我们选择它们中的较小者作为最终阈值。此外，阈值初始化为$1/C$（即，${\lambda }_0=1/C$），其中$C$是类别数量。因此，阈值最终调整为：
$${\lambda }_{iter}=\{\begin{array}{ll}\frac{1}{C}& \text{if }iter=0\\ \min ({\lambda }_{cnniter},{\lambda }_{mambaiter})& \text{otherwise}\end{array}$$
接下来，我们使用阈值生成分割掩码，包括一致区域的掩码 M c ∈ { 0 , 1 } W × H M_c \in \{0, 1\}^{W \times H} Mc​∈{0,1}W×H和不一致区域的掩码 M i c ∈ { 0 , 1 } W × H M_{ic} \in \{0, 1\}^{W \times H} Mic​∈{0,1}W×H：
$$M_c=[(1-U)>\lambda ]\wedge [(1-U)>\lambda ]$$
$$M_{ic}=\neg M_c$$
然后，掩码被用来从预测中分离出一致区域。预测概率分布图的不一致区域也被分离出来，并被视为后续EGC策略的证据。过程如下：
$$P_{ccnn}=P_{cnn}\odot M_c$$
$$P_{cmamba}=P_{mamba}\odot M_c$$
$$P_{eviiccnn}=P_{evicnn}\odot M_{ic}$$
$$P_{eviicmamba}=P_{evimamba}\odot M_{ic}$$
其中$\odot$表示逐元素乘法。

随后，我们进一步将不一致区域分离为可能接近决策边界的低证据预测和可能接近高密度区域的高证据预测。基于平滑性假设，两个网络分支的预测应该在高密度区域附近一致地表现出高证据。因此，我们专注于优化决策边界附近的低证据预测的概率分布。具体过程如下：我们首先比较$P_{eviiccnn}$和$P_{eviicmamba}$之间的证据大小，识别出$P_{eviiccnn}$中证据高于$P_{eviicmamba}$的区域。然后，我们锐化$P_{eviiccnn}$中高证据区域的预测概率分布，使其预测更接近高密度区域。最后，我们使用高证据预测来指导低证据预测。表达式如下：
$$M_{h}cnn=P_{eviiccnn}>P_{eviicmamba}$$
$$P_{eviichcnn}=P_{eviiccnn}\odot M_{h}cnn$$
$$P_{eviiclmamba}=P_{eviicmamba}\odot M_{h}cnn$$
$$P_{eviichhcnn}=(P_{eviichcnn}{)}^{1/\epsilon }$$
其中$\epsilon \in N>1$表示$P_{eviichcnn}$的$\epsilon$次根，用于锐化具有高证据的预测。类似地，$P_{eviicmamba}$中具有较高证据的区域被用来指导$P_{eviiccnn}$中具有较低证据的区域，可以表达如下：
$$M_{h}mamba=P_{eviicmamba}>P_{eviiccnn}$$
$$P_{eviichmamba}=P_{eviicmamba}\odot M_{h}mamba$$
$$P_{eviiclcnn}=P_{eviiccnn}\odot M_{h}mamba$$
$$P_{eviichhmamba}=(P_{eviichmamba}{)}^{1/\epsilon }$$

3.3. 损失函数

EGC的引导优化采用L2损失函数，表达如下：
$$L_{aEGC}={\ell }_{l2}(P_{eviiclmamba},\text{Odetach}(P_{eviichhcnn}))$$
$$L_{bEGC}={\ell }_{l2}(P_{eviiclcnn},\text{Odetach}(P_{eviichhmamba}))$$
其中$\text{Odetach}(\cdot )$表示与反向传播分离，${\ell }_{l2}(\cdot ,\cdot )$代表L2（也称为均方误差，MSE）损失函数，其计算公式如下：
$${\ell }_{l2}=\frac{1}{N}\sum _{i=1}^N(y_i-p_i{)}^2$$
其中$N$表示总像素数，$y_i$代表像素$i$的真值，$p_i$表示模型预测的像素$i$的概率。因此，不一致区域受EGC策略约束的损失计算如下：
$$L_{ic}=L_{aEGC}+L_{bEGC}$$
对于两个分支网络预测一致的区域，我们采用基于交叉熵的交叉伪监督方法来施加约束。首先，使用$\text{argmax}$函数$f_{\text{argmax}}(\cdot )$分别为两个分支的一致预测生成伪标签 Y ^ c c n n , Y ^ c m a m b a ∈ { 0 , 1 , … , K } W × H \hat{Y}_{c cnn}, \hat{Y}_{c mamba} \in \{0, 1, \ldots, K\}^{W \times H} Y^ccnn​,Y^cmamba​∈{0,1,…,K}W×H：
$${\hat{Y}}_{ccnn}=f_{\text{argmax}}(P_{ccnn})$$
$${\hat{Y}}_{cmamba}=f_{\text{argmax}}(P_{cmamba})$$
然后，一致区域的损失通过交叉伪监督[25]计算如下：
$$L_c={\ell }_{ce}(P_{ccnn},{\hat{Y}}_{cmamba})+{\ell }_{ce}(P_{cmamba},{\hat{Y}}_{ccnn})$$
其中${\ell }_{ce}$表示交叉熵损失函数，其计算公式如下：
$${\ell }_{ce}=-\frac{1}{N}\sum _{i=1}^N\sum _{k=1}^K{y}_{ki}\log (p_{ki})$$
其中$N$表示总像素数，$C$表示类别数。$y_{ki}$是指示变量，如果第$i$个样本属于第$k$个类别，则$y_{ki}=1$，否则$y_{ki}=0$。然后$p_{ki}$代表模型预测第$i$个样本属于第$k$个类别的概率。此外，对于涂鸦注释的像素，我们在两个分支的输出上使用部分交叉熵（pCE）监督，同时忽略未标记像素。并引入门控条件随机场（CRF）损失来减轻无关像素对当前像素分类的影响。这有助于模型更好地感知输入图像中的形态信息，从而强调语义边界。因此，两个分支网络的预测的监督损失计算如下：
$$L_{cnnsup}={\ell }_{pce}(P_{cnn},Y)+\gamma {\ell }_{crf}(P_{cnn})$$
$$L_{mambasup}={\ell }_{pce}(P_{mamba},Y)+\gamma {\ell }_{crf}(P_{mamba})$$
其中${\ell }_{pce}$表示部分交叉熵（pCE）损失函数，其计算公式与CE损失函数相似，不同的是$N$表示标记涂鸦的总像素数，未标记区域的像素不贡献于计算。 Y ∈ { 0 , 1 , … , K } W × H Y \in \{0, 1, \ldots, K\}^{W \times H} Y∈{0,1,…,K}W×H代表涂鸦注释的标签，$\gamma$表示权重。门控CRF损失函数的计算公式如下：
$${\ell }_{crf}=\sum _{i=1}^N\sum _{j=1}^N{w}_{ij}\varphi (x_i,x_j)(p_i-p_j{)}^2$$
其中$N$表示总像素数，$w_{ij}$表示门控函数以掩盖意外像素位置，函数$\varphi (\cdot ,\cdot )$用于量化像素$x_i$和$x_j$之间的相似性。此外，$p_i$和$p_j$分别代表像素$i$和$j$的预测概率值。在EDL中，由于使用Dirichlet分布来表示类别概率，因此不能直接使用交叉熵损失函数进行优化。相反，优化目标转移到Dirichlet分布的期望交叉熵损失。直接计算这个积分可能是具有挑战性的，因此使用Dirichlet分布的均值作为预测概率分布：
$${\ell }_{ece}={\mathbb{E}}_{D(pi|{\alpha }_i)}[-\sum _{k=1}^K{y}_{ki}\log (p_{ki})]=\sum _{k=1}^K{y}_{ki}(\psi (S_i)-\psi ({\alpha }_{ki}))$$
其中$\psi (\cdot )$是digamma函数。ECE鼓励为正样本在各个类别中生成证据。此外，为了减少负样本的证据，KL散度被用来惩罚负样本的生成证据：
$${\ell }_{kl}=\text{KL}(D(pi|{\alpha }_i)||D(pi,1))=\log \left[\frac{\Gamma ({\sum }_{k=1}^K{\alpha }_{ki})}{\Gamma (K){\prod }_{k=1}^K\Gamma ({\alpha }_{ki})}\right]+\sum _{k=1}^K({\alpha }_{ki}-1)\left[\psi ({\alpha }_{ki})-\psi \left(\sum _{k=1}^K{\alpha }_{ki}\right)\right]$$
$${\bar{\alpha }}_i=y_i+(1-y_i)\odot {\alpha }_i$$
其中$\Gamma (\cdot )$表示gamma函数，$D(pi,1)$是均匀Dirichlet分布，${\bar{\alpha }}_i$表示在去除误导性证据后样本$i$的预测参数${\alpha }_i$的Dirichlet参数。因此，总监督损失计算如下：
$$L_{sup}=L_{cnnsup}+L_{mambasup}+L_{pedl}$$
最终，以下联合目标函数与涂鸦注释一起优化以训练模型：
$$L_{all}=L_{sup}+L_{ic}+L_c$$

4. 实验和结果

4.1. 数据集

我们验证了所提出的方法在四个常见的公共超声数据集上的性能，这些数据集专门用于分割任务，分别是CardiacUDA[26]、EchoNet[27]、BUSI[28]和DDTI[29]，并与其他方法进行了比较。这些数据集涵盖了乳房、甲状腺和心脏等多种解剖区域，包括二元和多类分割任务。CardiacUDA：CardiacUDA数据集来自两家匿名医院，包括经过5-6名经验丰富的医生批准的精心收集和注释的病例。每位患者接受了四个视图的扫描：胸骨旁长轴左心室（LVLA）、肺动脉长轴（PALA）、左心室短轴（LVSA）和心尖四腔（A4C），每位患者产生四个视频。视频分辨率范围从800×600到1024×768不等，具体取决于扫描仪（Philips或Hitachi）。该数据集大约包括来自每家医院100名患者的516和476个视频。每个视频包含100多帧，覆盖至少一个心脏周期，每五个视频中有五帧被注释为左心室（LV）、右心室（RV）、左心房（LA）和右心房（RA）。EchoNet：EchoNet-Dynamic数据集包括10030个心尖四腔超声心动图视频，这些视频来源于2016年至2018年在斯坦福医院进行的临床扫描。这些视频已经被预处理以排除非必要内容，调整大小至112×112像素，并在收缩末期和舒张末期注释左心室心内膜边界。我们从在线分享这些注释帧的同行那里获得了这些注释，并将它们用作本研究图像分割任务的分割目标，形成了一个新的数据集。这个分割数据集包含20046张图像，每张图像都附有相应的分割图。BUSI：乳房超声图像（BUSI）数据集，于2018年获得，包括来自600名25至75岁女性患者的780张乳房超声图像，平均图像大小为500×500像素。它包括正常、良性和恶性乳腺癌病例的超声图像，以及相应的分割图。DDTI：数字甲状腺超声图像数据库（DDTI），是科学界公开资源，由哥伦比亚国立大学、CIM@LAB和医学诊断研究所（IDIME）支持，包括99个案例，134张图像，涵盖甲状腺炎、囊性结节、腺瘤和癌症。我们的研究使用了MICCAI 2020 TNSCUI挑战赛第一名解决方案的作者提供的预处理版本，他们清洁、裁剪并移除了无关区域。

4.2. 实施细节和评估指标

对于本研究，BUSI和DDTI来源的图像被调整为256×256像素以保持一致性。对于BUSI数据集，我们仅使用带有病变和分割掩码的样本，丢弃了没有分割目标的正常样本。此外，对于具有多个病变区域的样本，分割掩码被合并。对于EchoNet数据集，我们使用原始大小，即112×112像素的图像。此外，从CardiacUDA提取的注释帧被调整为256×256像素的新分割数据集，包括2250张图像。所有的涂鸦注释都是由HiLab在UESTC提供的代码2生成的。在生成的注释中，背景类别被表示为0，未标记的类别被表示为K（即不包括其他类别的最大数）。我们生成的涂鸦注释相对稀疏。我们使用五折交叉验证评估了所有方法在所有数据集上的性能。训练模型使用的优化器是随机梯度下降（SGD），权重衰减为$10^{-4}$，动量为0.9，以最小化联合目标函数方程54。我们基于Python 3.8、PyTorch 1.12和WSL4MIS代码库2实现了我们提出的方法和其他比较方法，并在装有2个Nvidia Geforce RTX 3080 GPU的服务器上进行了训练，总计20GB内存。图像在训练前进行了预处理，包括随机水平或垂直翻转、随机角度旋转、随机均衡、随机调整亮度、对比度、饱和度和色调。学习率由多项式学习率调度器[10]在线调整：
$$L{R}_{iter}={\left(1.0-\frac{iter}{ite{r}_{max}}\right)}^{0.9}L{R}_0$$
其中$L{R}_{iter}$表示第$iter$次迭代的学习率。批量大小和总迭代次数（$iter$）分别设置为12和60k。超参数$\tau$、$\epsilon$和$\gamma$分别设置为0.25、0.5和0.1。为了公平比较，我们在测试阶段仅使用U-Net的输出作为最终结果，不应用任何后处理方法。所有实验都在相同的实验环境中进行。我们使用4个在弱监督或半监督医学图像分割任务中广泛采用的指标来定量评估所有方法。评估指标包括Dice分数、Jaccard指数、平均表面距离（ASD）和95% Hausdorff距离（95HD）。Dice分数和Jaccard指数评估了真值和预测之间的像素级重叠，而ASD和95HD测量了它们之间的表面距离。注意，对于CardiacUDA数据集上的多类分割任务，我们仅呈现了Dice和95HD作为评估指标。

4.3. 与现有方法的比较

本小节比较了我们提出的MambaEviScrib与4个不同数据集上的5种先进的涂鸦监督学习方法。这些方法包括pCE[16]、USTM[49]、Gated CRF[17]、DMPLS[10]、ScribbleVC[47]和ScribFromer[48]。pCE作为基线方法，为所有方法设定了下限。USTM和Gated CRF的骨干是U-Net架构，而ScribbleVC和ScribFromer都融合了Transformers。此外，训练了完全监督的U-Net[6]作为参考。值得注意的是，尽管我们的方法包含了U-Net和Mamba-UNet，但在测试或推理阶段仅需要U-Net。

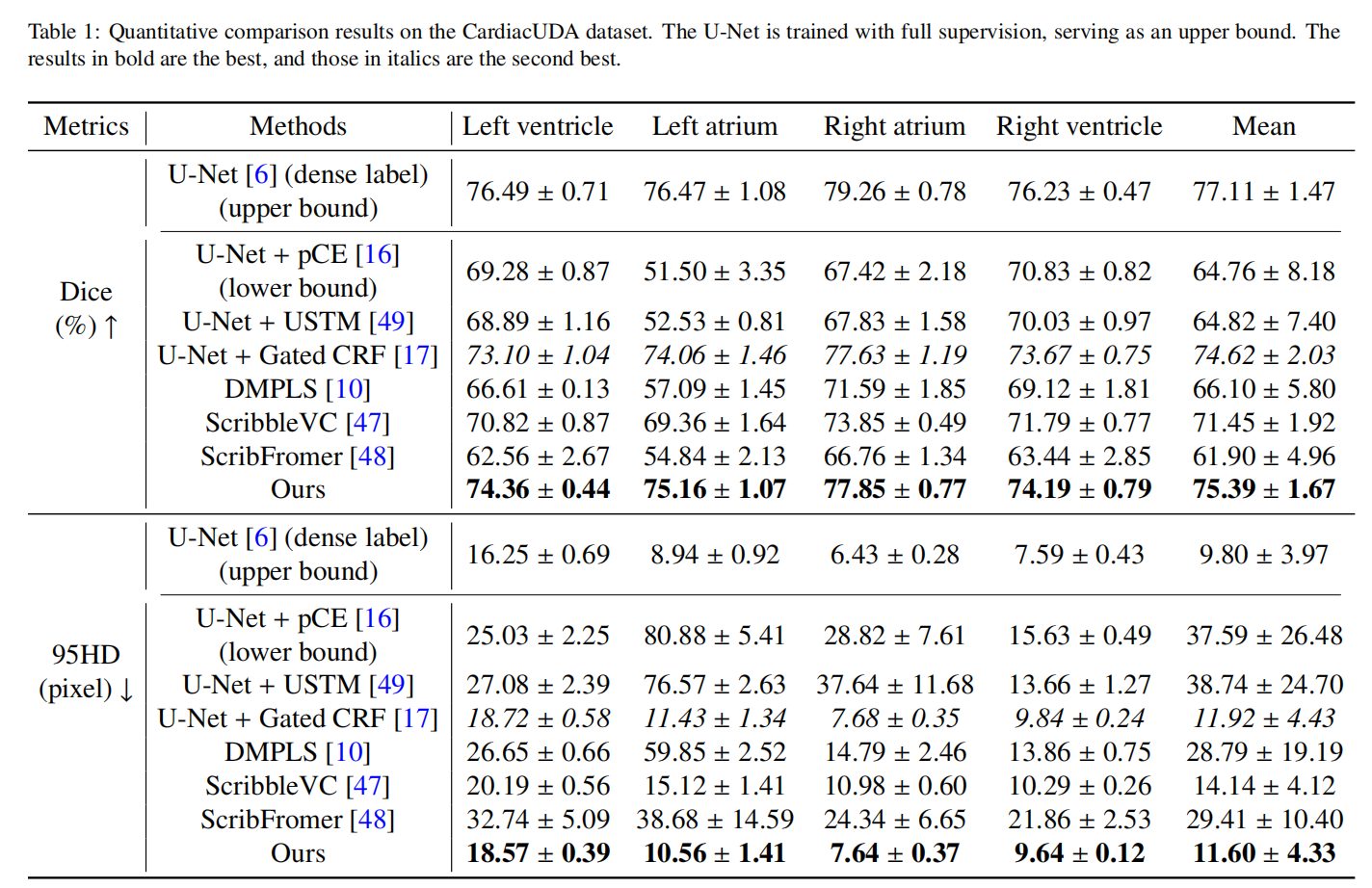
4.3.1. 在CardiacUDA数据集上的结果

所有方法在CardiacUDA数据集上的实验定量结果如表1所示。从表中可以看出，基线方法pCE表现平庸，为涂鸦监督分割性能设定了基准。所有其他方法的表现都超过了pCE。在现有方法中，Gated CRF表现出色，仅次于提出的方法，平均Dice分数为74.62%，95HD为11.74。这表明Gated CRF在超声数据集的涂鸦监督分割任务中具有优势，归因于其感知解剖结构形态特征的能力。我们提出的方法在所有评估指标上都取得了最佳性能，平均Dice分数为74.62%，95HD为11.74，超过了Gated CRF 0.77%的Dice分数。这可能源于模型倾向于优先学习易于分割的类别，从而引入了不公平性。相比之下，我们的方法不仅在整体上取得了优越的分割性能，而且在不同类别之间的性能差距较小，突出了其优越性和鲁棒性。

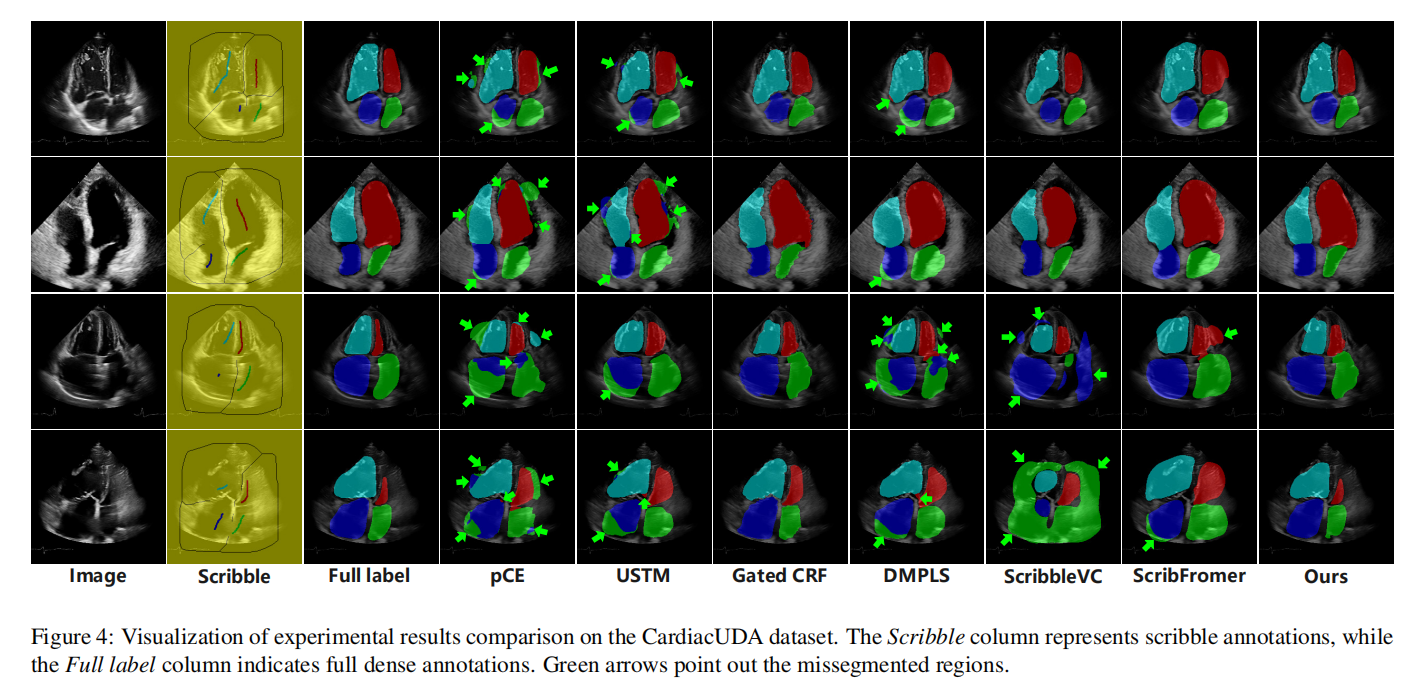
我们可视化了分割结果，如图4所示，旨在清晰直观地理解各种方法之间的性能差异。图中的绿色箭头指出了分割错误区域。从图中可以看出，第一行和第二行的图像质量较高，边界更清晰，因此总体分割结果更好。大多数分割方法在第三行和第四行的图像中犯了错误，而我们的方法避免了严重错误，即误识别解剖结构位置。相对而言，pCE、USTM和DMPLS显示出更多的分割错误区域。我们的观察发现，最常见的错误是将其他心脏腔室误识别为左心房，可能归因于左心房在大多数超声心动图图像中所占比例较小，使得弱监督模型难以充分捕捉左心房的特征。此外，我们观察到ScribbleVC在分割某些区域（如图中的左、右心室）时趋于保守，未能完全描绘目标对象。相反，它在其他区域（如图中的左、右心房）的分割中表现出更激进的分割，错误地将大量非目标区域包含在分割中。尽管据报道在磁共振图像分割中表现优异[47]，但可能不适应超声图像的分割。

总之，我们的MambaEviScrib在多类分割超声心动图方面表现出色，减少了严重错误，并总体上提高了分割精度。此外，我们的方法更准确地描绘了边缘细节，表明其对全局形态特征的感知能力。

4.3.2. 在EchoNet数据集上的结果

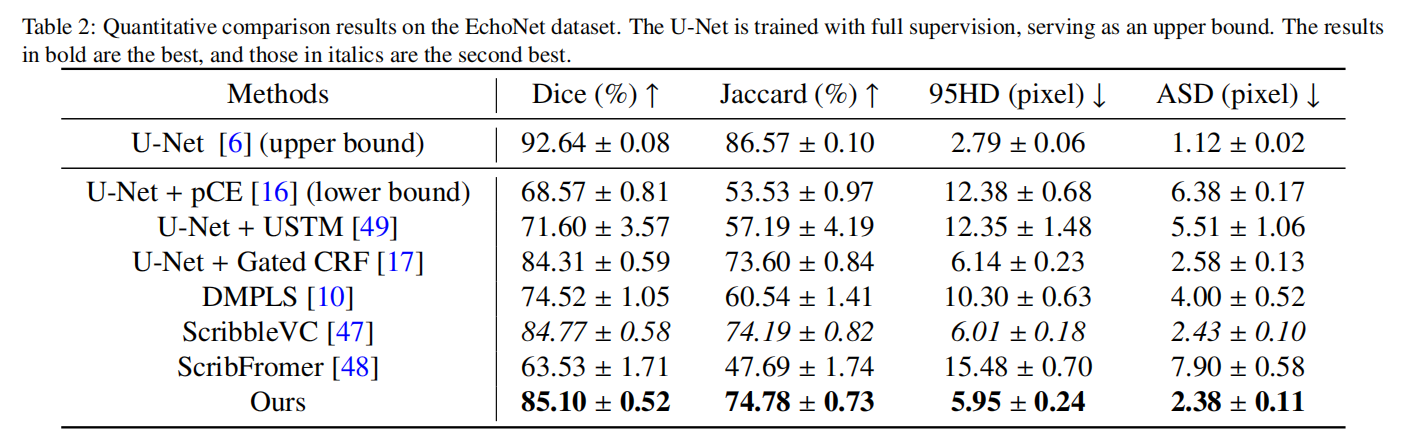
我们还在另一个超声心动图数据集EchoNet上进行了比较实验，定量结果如表2所示。pCE仍然是基线方法。令人惊讶的是，ScribFormer在该数据集上表现不佳，甚至低于基线。这可能归因于注释信息有限，阻止了它准确捕捉分割对象的特征，如形态和边缘。大多数其他方法超过了基线方法，ScribbleVC表现良好，仅次于我们的方法，Dice分数和95HD分别为84.77%和6.01。与在CardiacUDA数据集上的表现相比，在该数据集上，ScribbleVC超过了Gated CRF方法，使后者降至第三位。我们的方法表现最佳，Dice分数为85.10%，95HD为5.95，尽管与完全监督方法相比存在差距，但重要的是，这是在极其稀疏的涂鸦注释的前提条件下实现的，这些注释构成了被分割对象的一小部分，带来了巨大挑战。此外，面对EchoNet数据集中变化的左心室形状，我们的方法表现出令人满意的性能，表明其能够捕获全局信息和形态特征。

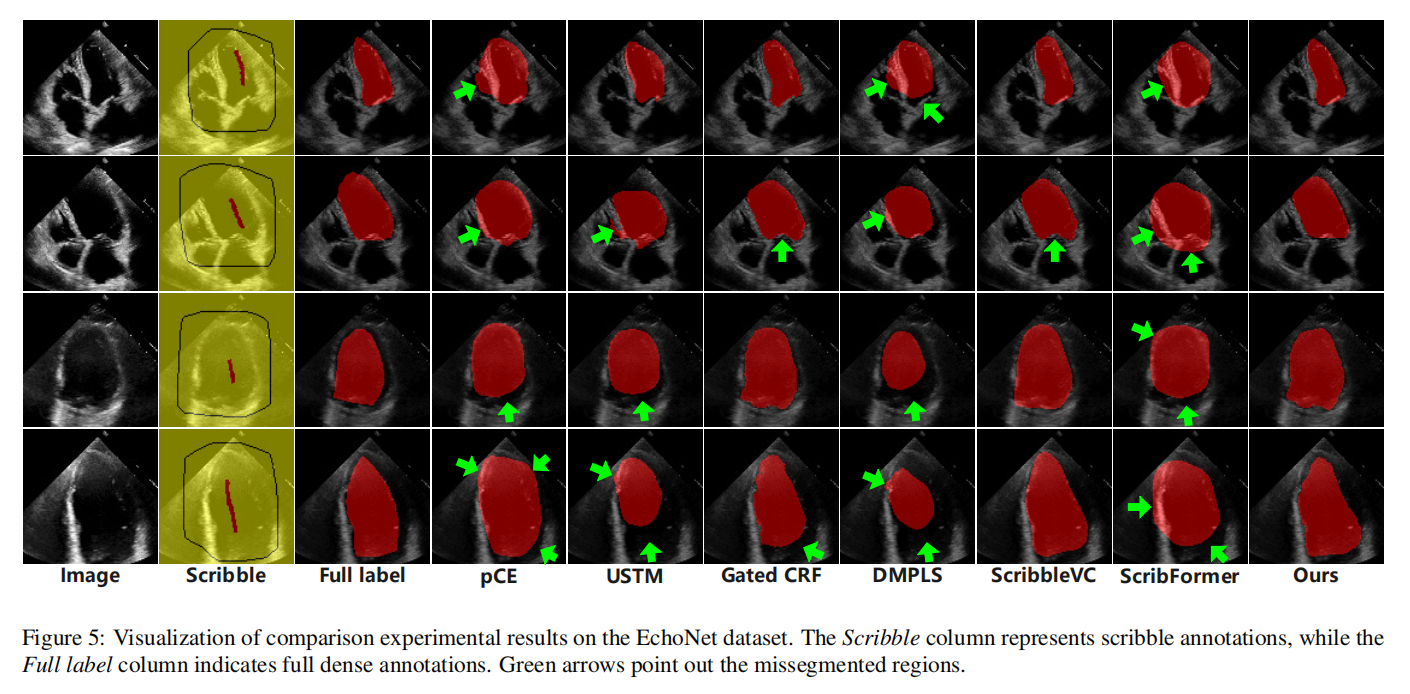
所有分割结果如图5所示。我们选择了四个不同大小的左心室超声心动图图像，并从上到下按大小顺序排列。图中的绿色箭头指出了分割错误明显的区域。从图中可以看出，一些方法在分割时趋于激进，特别是处理小左心室时。在大尺寸左心室的情况下，USTM和DMPLS等方法显示出明显的保守分割趋势，显著损害了解剖描绘的精度。这表明这些方法在充分捕获全局信息方面存在不足。在这两种方法中，ScribFormer的分割区域明显比DMPLS更激进，我们假设这可能受到Transformer架构的影响。尽管如此，它们仍然不足以充分捕获形态特征。此外，我们注意到一些方法未能分割被二尖瓣覆盖的区域，将其从左心室中排除。我们推测这可能是由于该区域的涂鸦注释覆盖不足，导致模型无法捕捉其特征。总之，我们的方法能够克服上述大部分问题，在超声数据方面展现出优势。

4.3.3. 在BUSI数据集上的结果

除了超声心动图数据外，我们还在乳房超声数据集BUSI上进行了比较实验，结果如表3所示。在现有方法中，Gated CRF方法继续保持最佳表现，Dice分数为71.39%，显著优于基线方法pCE。然而，我们提出的方法超过了Gated CRF，Dice分数为74.62%，比Gated CRF提高了3.23%，并进一步缩小了与完全监督上限77.91%的差距。我们的方法在四个数据集中的这个数据集上表现出最大的改进，表明在乳房病变检测中具有一定的优势。

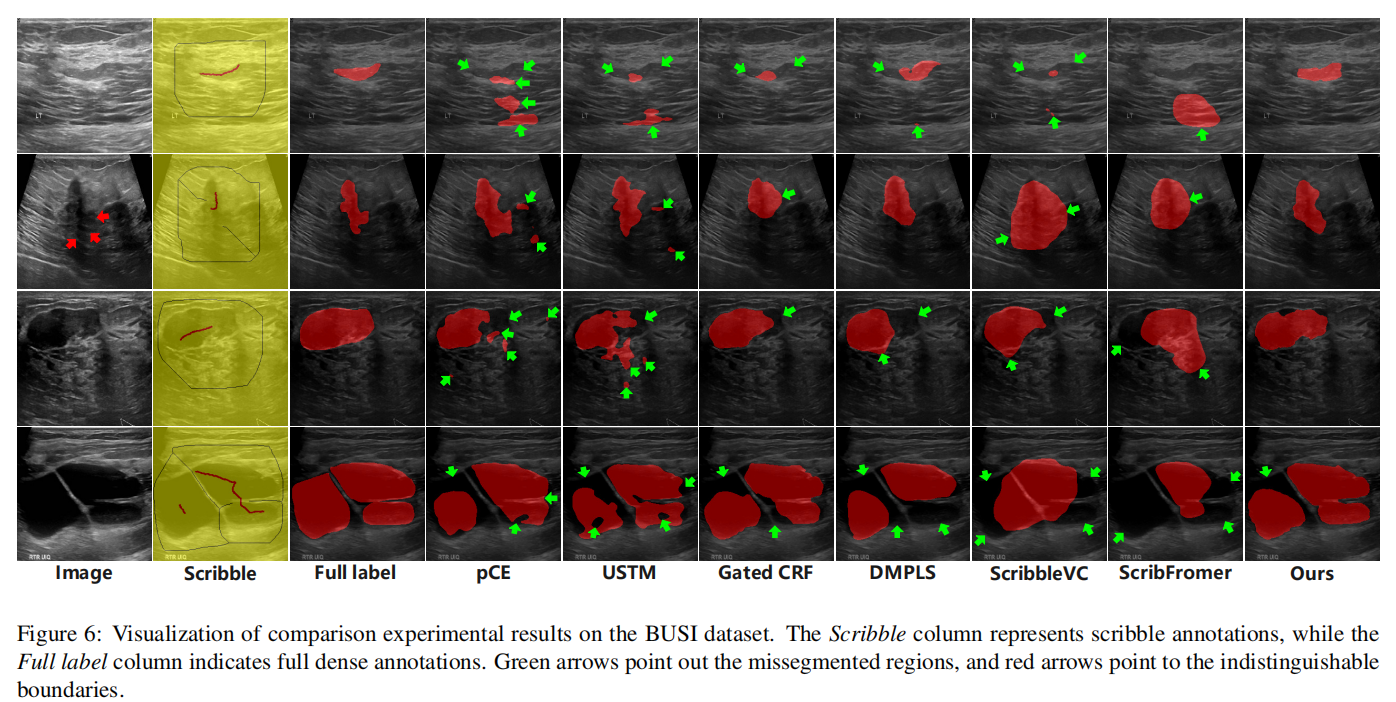
所有分割结果如图6所示。我们选择了一组代表性的图像及其相应的分割结果，包括不同形态和大小的病变，进行了展示。第一行图像中的病变相对较小，对一些方法来说是一个挑战，它们倾向于错误地将类似区域分割为病变，导致假阳性，而其他方法可能未能完全分割病变，导致假阴性。第二行图像中的病变下边界不清晰（由红色箭头指示），即使对人类眼睛来说也难以辨认，阻碍了一些方法准确分割边界。第四行图像中的病变由多个相邻病变组成，这在数据集中相对罕见。因此，大多数方法难以准确捕捉其形态特征。此外，该病变的尺寸较大，需要模型具备理解全局信息的能力。虽然我们的方法并未达到完美，但它优于现有方法。从可视化结果来看，pCE和USTM方法在该数据集中的一些图像中分割出相对较多的假阳性病变，这比我们的方法差。

4.3.4. 在DDTI数据集上的结果

我们还在另一个具有挑战性的数据集DDTI上进行了甲状腺结节超声图像分割的实验，结果如表4所示。在这个数据集上，Gated CRF方法继续在现有方法中保持最佳表现，而USTM方法不幸再次低于基线。我们的方法继续超越其他方法，Dice分数为68.04%，比Gated CRF方法提高了1.51%。然而，与上限相比仍有差距，这归因于该数据集对弱监督的巨大挑战。

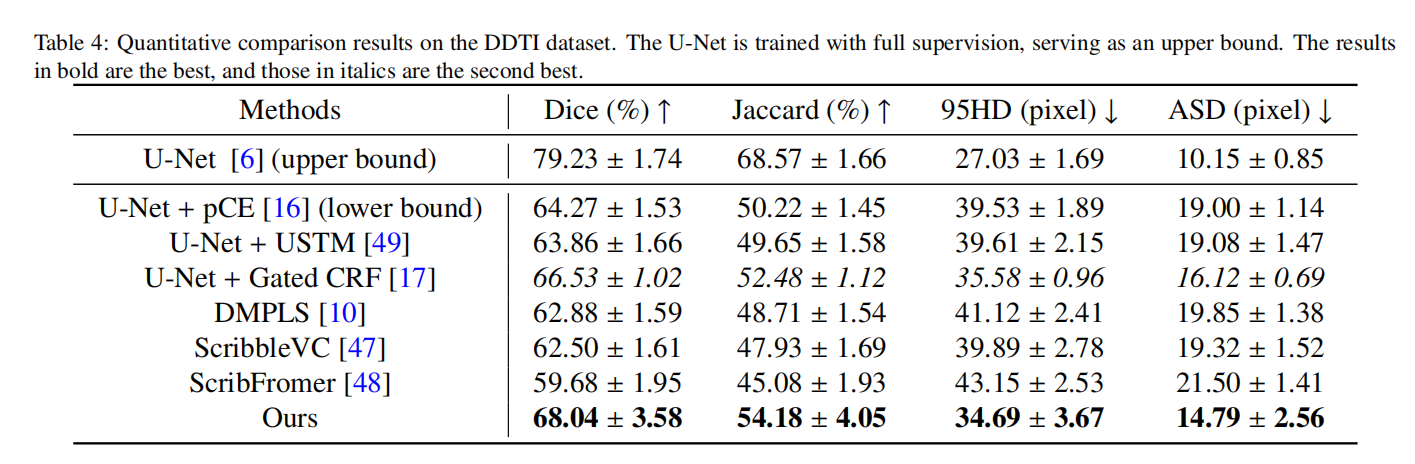
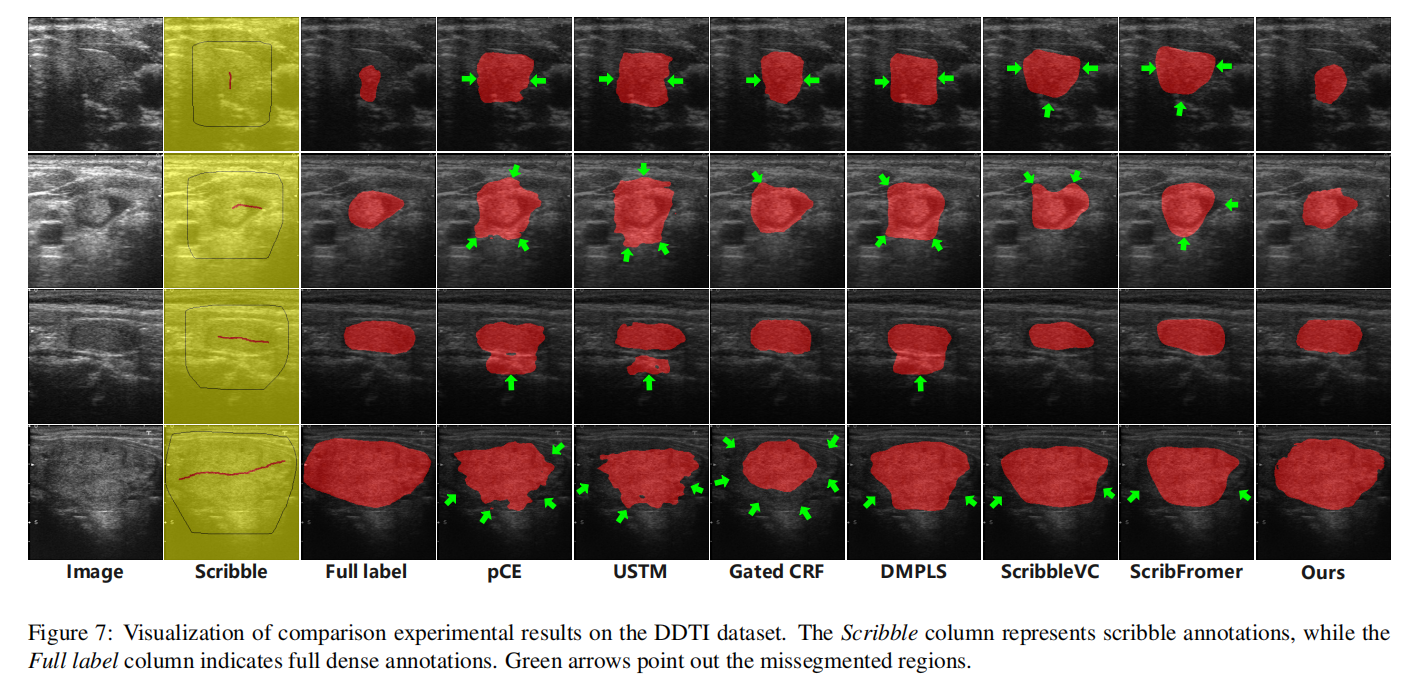
所有分割结果如图7所示，所选病变从大小上排列。一些方法倾向于对小尺寸病变产生假阳性，对大尺寸病变产生假阴性。总体而言，我们的方法相比现有方法表现更好。然而，观察四个可视化示例中的超声图像，可以明显看出病变边界不清晰，难以区分病变和正常组织。这对弱监督分割来说是一个重大挑战，并强调了未来超声图像分割领域需要持续关注和改进的必要性。

4.4. 消融研究

4.4.1. 双分支网络的比较

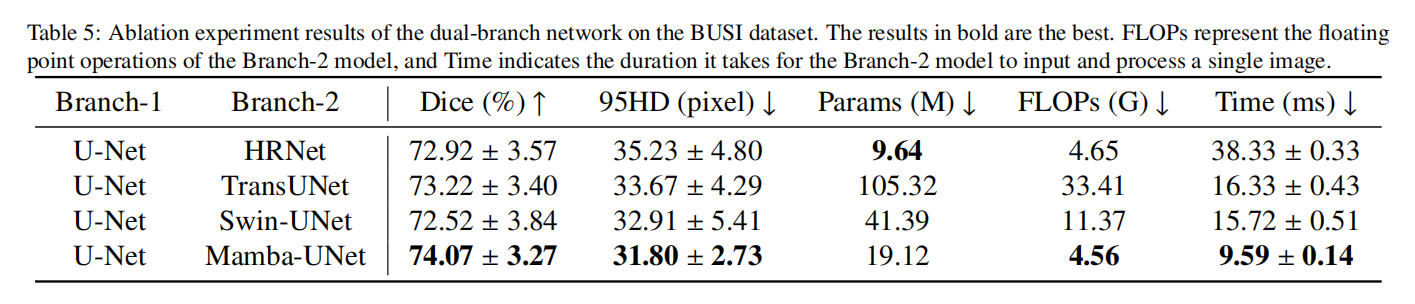
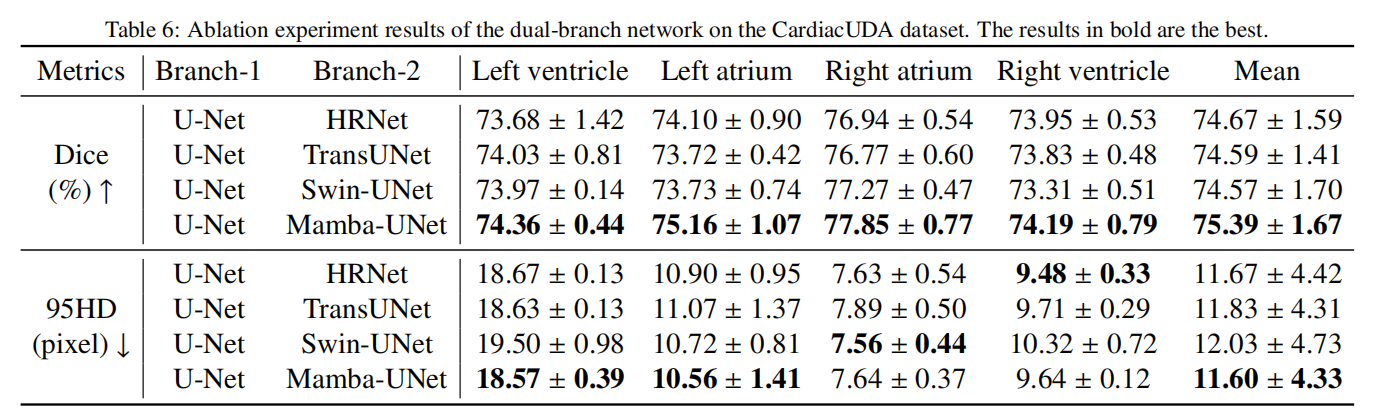
为了证明Mamba-UNet在我们提出的方法中的Mamba分支中的优越性，我们进行了实验，用其他先进网络替换了它。这些网络包括利用Transformer架构的Swin-UNet和TransUNet，以及纯基于CNN的HRNet。我们在BUSI和CardiacUDA数据集上比较了它们的表现和效率。为了公平，测试阶段仅使用U-Net进行推理。实验结果如表5和表6所示，我们的方法以第二少的参数数量实现了最佳性能，仅次于HRNet。然而，在浮点运算（FLOPs）方面，我们的方法甚至超过了基于CNN的HRNet，记录了最低的FLOPs 4.56G。此外，我们的方法以最快的速度运行，大约需要9.59ms来处理和分割一个256×256像素的输入图像，比第二快的Swin-UNet快1.64倍。这突显了Mamba模型在显著降低计算复杂性的同时有效捕获长期依赖性的能力。

4.4.2. 一致性策略的比较

为了验证EDL和EGC的有效性，我们在BUSI和CardiacUDA数据集上进行了消融实验，实验结果如表7和表8所示。鉴于EGC依赖于EDL，我们首先从框架中移除EGC，并用传统的均方误差（MSE）约束替换它，以验证EGC的优越性。根据实验结果，我们完整的方法优于移除EGC或同时移除EGC和EDL的条件。具体来说，与同时移除EGC和EDL的条件相比，我们完整的方法在BUSI数据集上实现了1.32%更高的Dice分数，在CardiacUDA数据集上实现了1.49%更高的Dice分数。总之，提出的EGC展现了一定的优势，帮助模型更好地处理位于决策边界的像素，例如超声图像中的模糊边缘，从而提高性能。

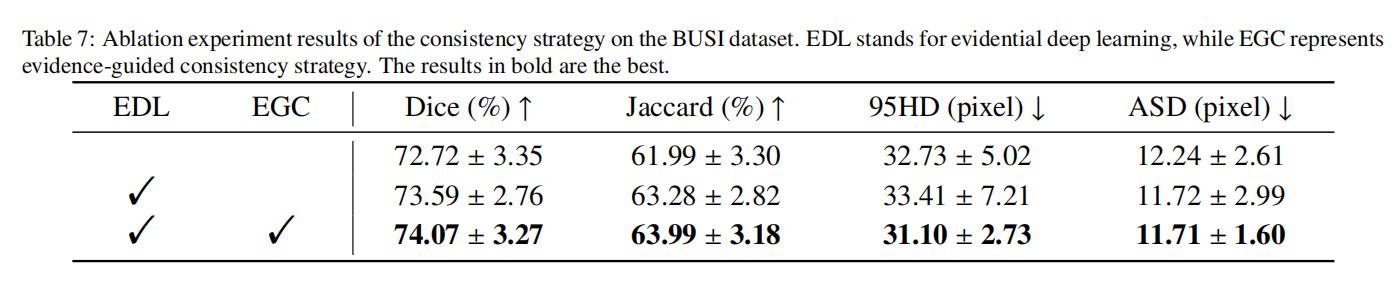
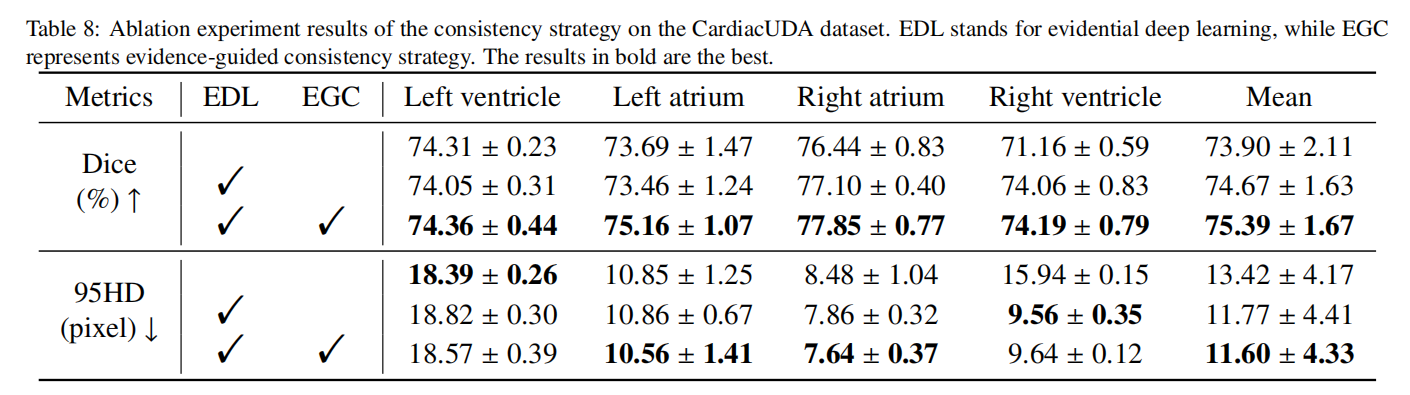
4.4.3. 超参数分析

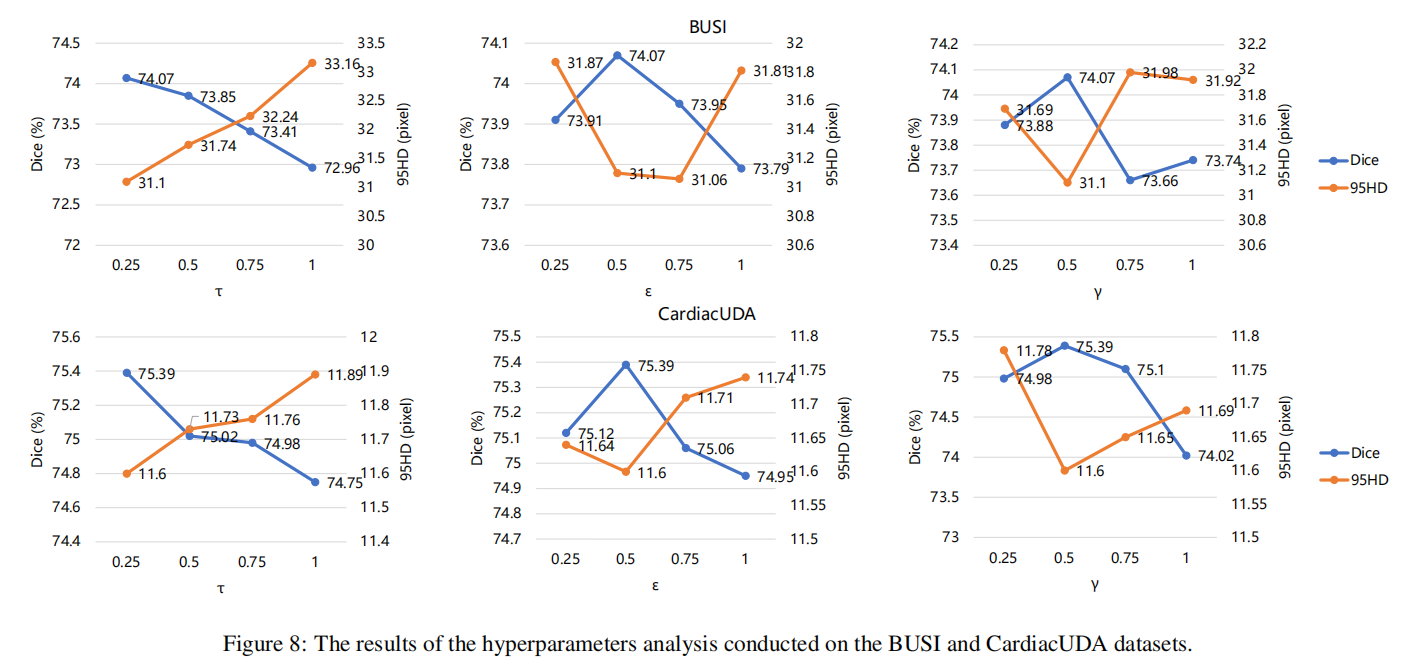
我们对需要手动调整的3个超参数进行了分析，即$\tau$、$\epsilon$和$\gamma$。参数$\tau$作为转换函数$f_e(\cdot )$（见方程10）中的缩放因子，调节函数的平滑度。$\epsilon$作为方程30和34中的锐化温度，使高证据预测偏向更高密度区域。参数$\gamma$在方程43和44中作为损失函数pCE和Gated CRF之间的平衡权重。如图8所示，当$\tau$、$\epsilon$和$\gamma$分别设置为0.25、0.5和0.1时，模型实现了最佳性能。总之，这些超参数的设置变化对模型的性能有一定的影响，其中$\epsilon$的影响最小，Dice差异最大仅为0.44%，而$\gamma$的影响更大，Dice差异最大为1.37%。这种差异可能归因于Gated CRF损失的影响力。

4.5. 泛化和鲁棒性分析

4.5.1. 泛化分析

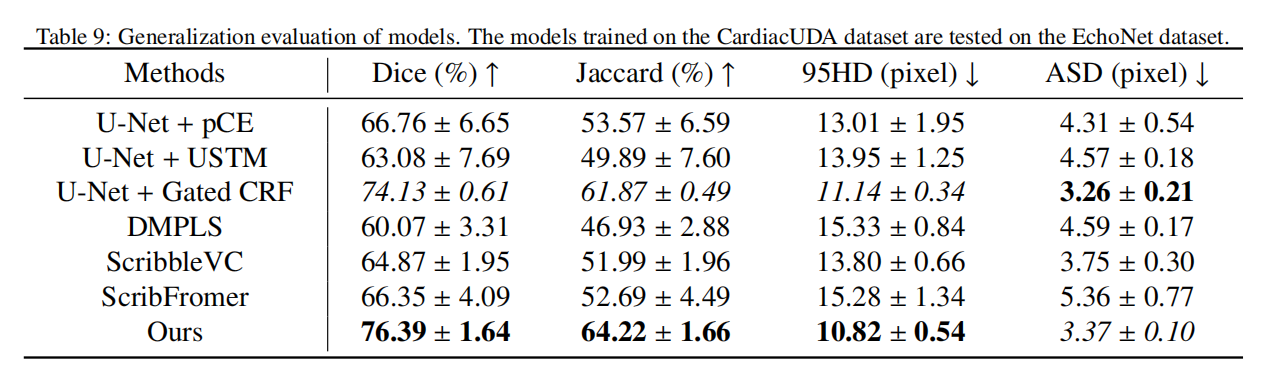
为了评估每个模型的泛化能力，我们将在CardiacUDA数据集上训练的模型应用于EchoNet数据集的测试，该数据集作为分布外（OOD）数据集。这对于将模型应用于现实世界临床场景至关重要。由于EchoNet数据集专门用于分割左心室，而CardiacUDA数据集包括所有四个心脏腔室，包括左心室，因此在EchoNet数据集的测试中仅保留了左心室分割结果。此外，鉴于CardiacUDA数据集中的图像大小为256×256像素，而EchoNet数据集中的图像为112×112像素，所有图像首先被上采样到256×256像素，然后才在EchoNet数据集上进行测试。随后，获得的预测掩码被缩放回112×112像素，之后计算评估指标。评估结果如表9所示。结果表明，在现有方法中，Gated CRF方法表现最佳，而其他现有方法甚至低于基线pCE方法，表明它们泛化能力不足，可能存在过拟合问题。相比之下，我们的方法优于所有其他方法，Dice分数比第二好的Gated CRF方法高出2.26%，显示出其优越的泛化能力。这是因为证据理论为EDL提供了坚实的数学基础，使模型能够准确量化预测不确定性。证据损失函数指导模型在最小化预测错误的同时，也最小化对不确定性的低估或高估。这种稳健的学习过程使模型能够学习更泛化的特征表示，而不仅仅是记忆训练数据中的噪声或特定模式。

4.5.2. 鲁棒性分析

在现实世界的临床场景中应用模型时，它们有时需要面对噪声数据。因此，有必要在噪声数据上测试模型的性能以验证其鲁棒性。我们在BUSI数据集和CardiacUDA数据集上应用高斯噪声来降低图像质量，模拟低质量数据采集的场景。我们考虑了三个不同水平的高斯噪声，分别以标准差$\sigma$的0.05、0.1和0.15为特征，在图像像素被归一化到0到1的范围内。从实验结果（表10和表11）来看，当$\sigma =0.05$时，所有方法的性能下降相对较小，而我们的方法保持最佳性能，Dice分数仅下降了0.31%。当$\sigma$增加到0.1时，我们的方法仍然是最佳且性能下降最小的。然而，在$\sigma$达到0.15的极端条件下，尽管大多数方法经历了显著的性能下降，我们的方法仍然保持优势，表现出最佳性能且下降最小。

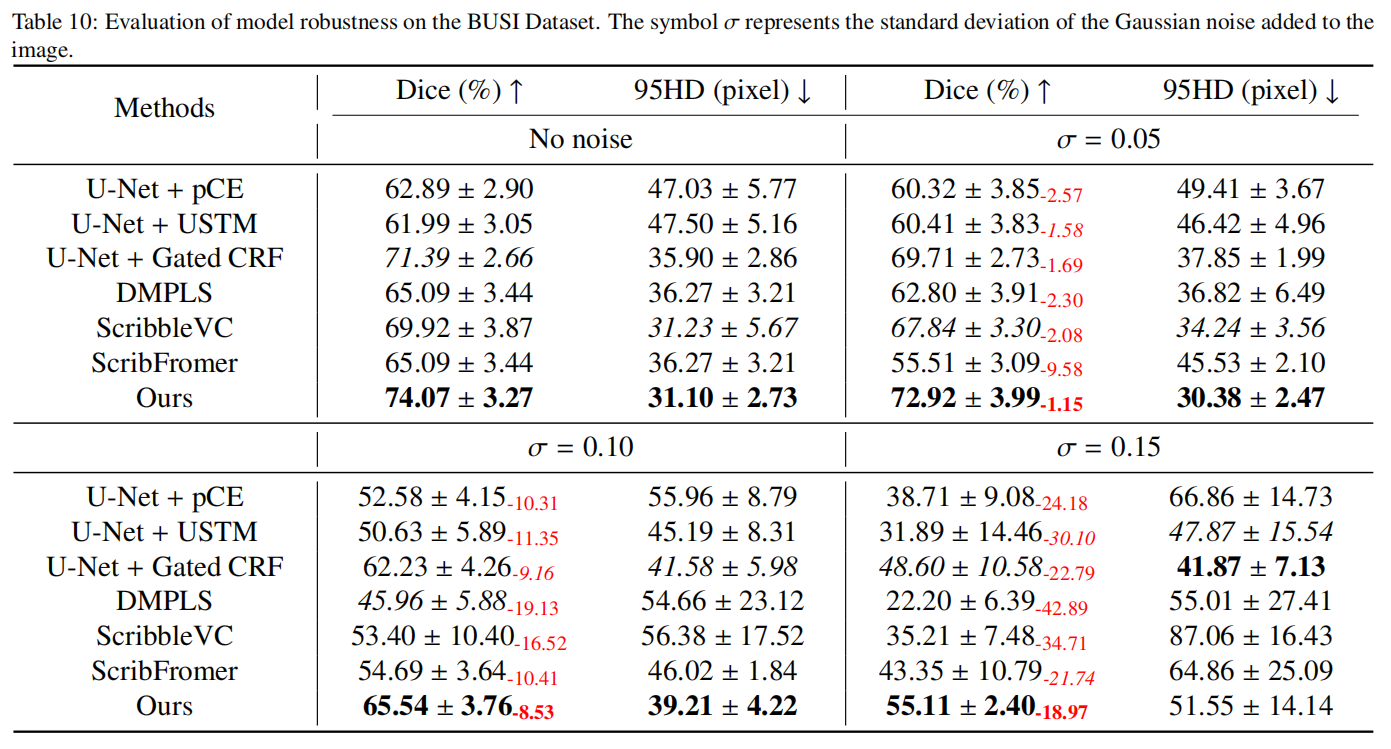
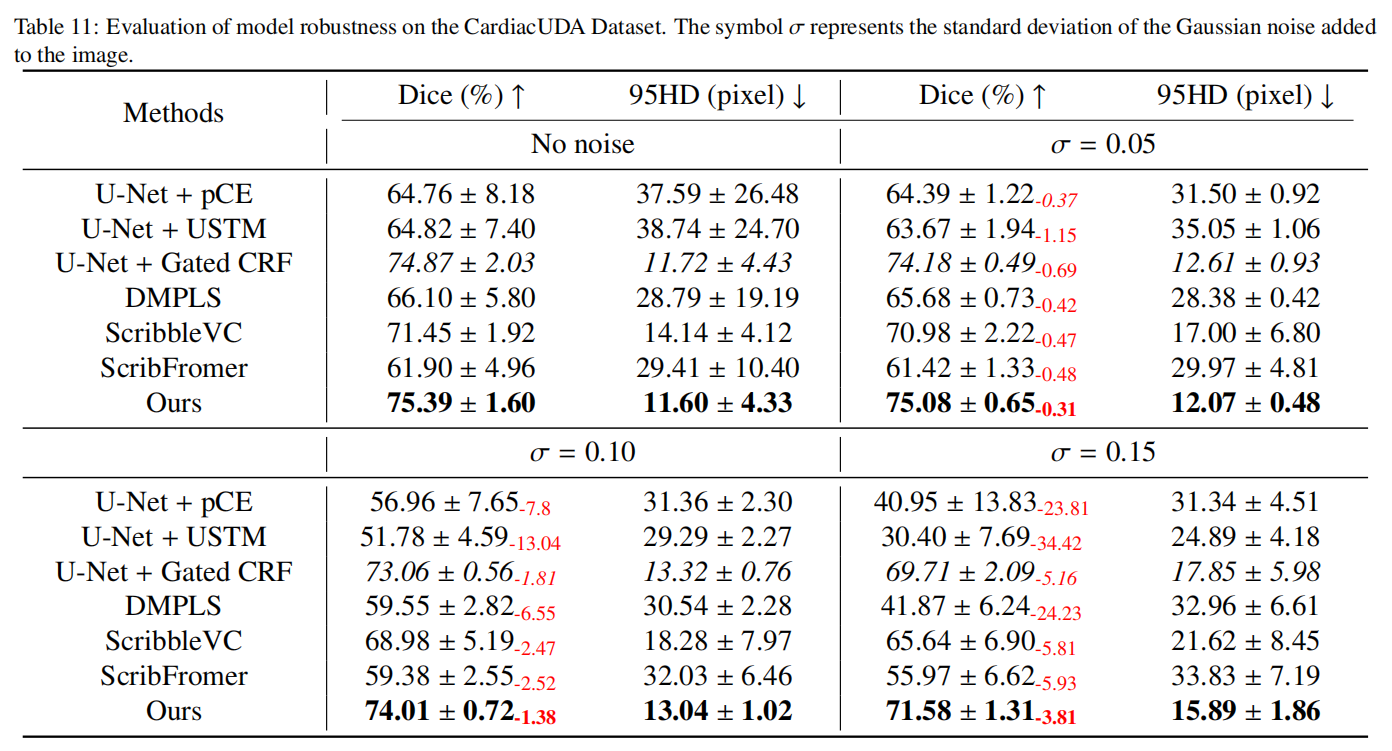
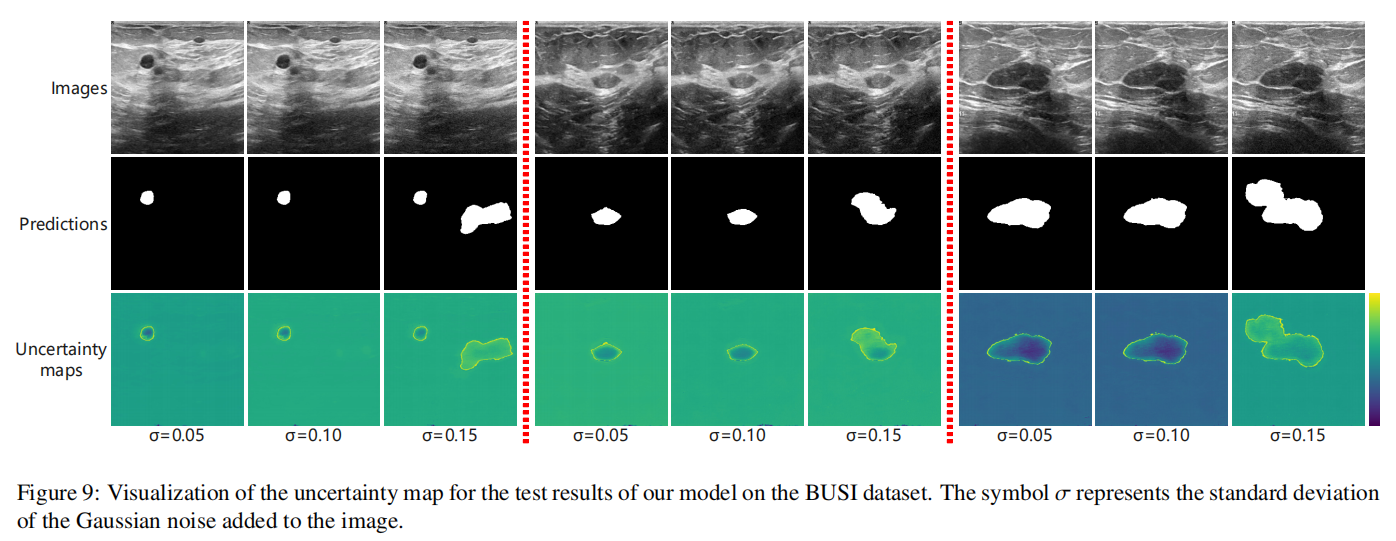
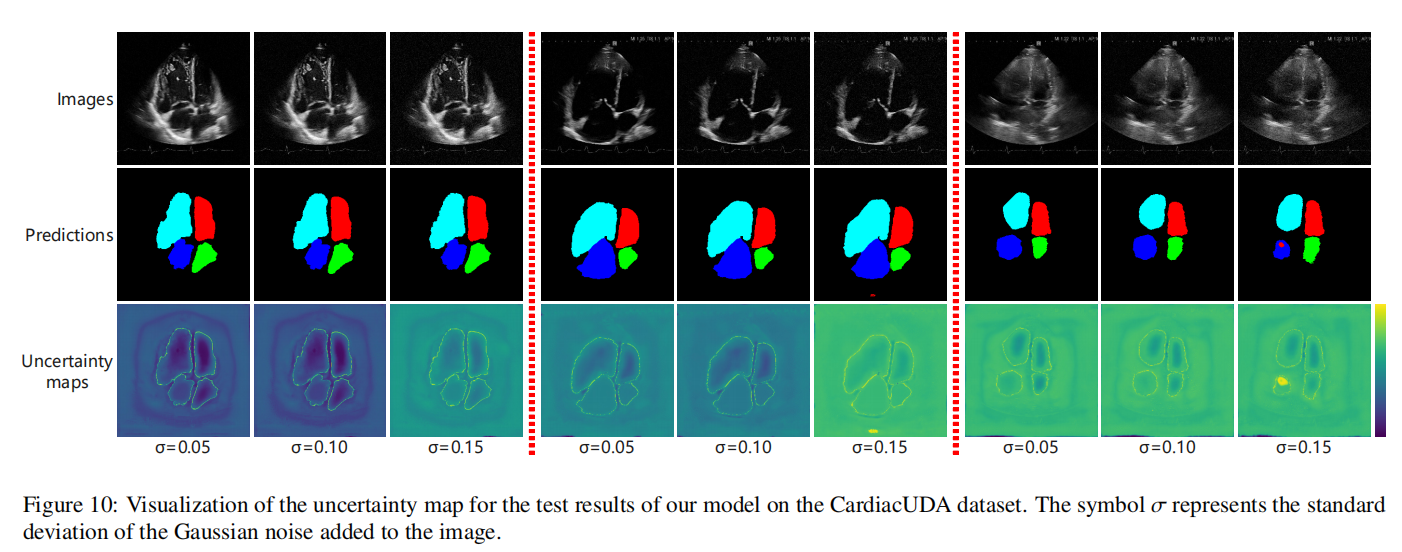
具体来说，在BUSI数据集上，我们的方法比表现最差的DMPLS的Dice分数高出32.91%，显示出显著的优势。在CardiacUDA数据集上，我们的性能下降仅为3.81%。我们观察到模型在BUSI和CardiacUDA数据集之间的性能下降存在显著差异，随着噪声水平的增加，模型在BUSI上的性能下降更为明显。我们假设这可能归因于多类数据提供的更丰富的监督信息。鉴于类别数量更多，模型可能需要学习更复杂的特征来表示数据，使它们能够更好地适应并克服噪声的影响。总之，我们的方法表现出鲁棒性，因为Dirichlet分布能够对预测结果在不同类别上的信心分布进行建模，即概率的概率。这种方法通过引入证据理论来量化预测不确定性，提供了更大的灵活性，使模型能够区分不确定性是来自数据噪声还是自身知识的局限性。这种对不确定性的显式建模帮助模型在面对复杂或异常输入时保持稳定。此外，我们可视化了不确定性图，如图9和图10所示。在大多数情况下，整体不确定性随着噪声的增加而增加。模型的预测在目标区域的边缘倾向于表现出更高的不确定性，而目标的内部区域通常显示出较低的不确定性。随着噪声的增加，一些区域可能被错误预测，但这些区域通常表现出高不确定性，可以从图中观察到。值得注意的是，图10显示了涂鸦注释对一些图像预测的显著影响，涂鸦注释的背景区域附近出现了低不确定性区域。这验证了我们不确定性估计的有效性，因为涂鸦注释区域内的预测应该是高度证据的。

5. 结论

本文提出了一种基于涂鸦的WSL方法，用于超声图像分割，有效降低了注释成本。引入的CNN-Mamba双分支网络有效地捕获了局部和全局特征，同时降低了计算复杂性。此外，基于EDL的EGC策略优化了模型对边缘区域的预测，保留了低置信度像素，并利用它们增强了目标边缘预测的稳定性。在四个公共超声图像数据集上的广泛实验表明，我们的方法在性能、泛化能力和鲁棒性方面优于现有的WSL方法，验证了我们方法的有效性及其在临床应用中的潜力。

声明

本文内容为论文学习收获分享，受限于知识能力，本文对原文的理解可能存在偏差，最终内容以原论文为准。本文信息旨在传播和学术交流，其内容由作者负责，不代表本号观点。文中作品文字、图片等如涉及内容、版权和其他问题，请及时与我们联系，我们将在第一时间回复并处理。