TMI 2024 | 基于扩散模型的脑图像反事实生成与异常检测

论文信息

题目：Diffusion Models for Counterfactual Generation and Anomaly Detection in Brain Images

基于扩散模型的脑图像反事实生成与异常检测

作者：Alessandro Fontanella, Grant Mair, Joanna Wardlaw, Emanuele Trucco, Amos Storkey

论文创新点

1. 弱监督方法：提出了一种弱监督方法，能够自动生成病变图像的健康版本，并利用它来获取像素级的异常图。该方法仅使用图像级标签，而不需要像素级注释。

2. 扩散模型结合：结合了去噪扩散概率模型（DDPM）和去噪扩散隐式模型（DDIM），在采样过程的每一步中对病变区域进行有针对性的修改，同时保留图像的其余部分。

3. 显著性图引导：使用ACAT生成的显著性图来引导图像生成过程，确保病变区域的修改基于周围的解剖结构。

4. 无缝融合：在每一步采样过程中，将DDPM和DDIM的结果进行无缝融合，确保生成的图像具有一致的外观，并在编辑和未编辑部分之间实现平滑过渡。

摘要

病理区域的分割掩码在许多医学应用中非常有用，例如脑肿瘤和卒中的管理。此外，健康的反事实图像可以用于增强放射科医生的训练文件，并提高分割模型的可解释性。在本研究中，我们提出了一种弱监督方法，用于生成病变图像的健康版本，并利用它来获取像素级的异常图。为此，我们首先使用ACAT生成一个大致覆盖病理区域的显著性图。然后，我们提出了一种技术，允许对这些区域进行有针对性的修改，同时保留图像的其余部分。具体来说，我们使用在健康样本上训练的扩散模型，并在采样过程的每一步结合去噪扩散概率模型（DDPM）和去噪扩散隐式模型（DDIM）。DDPM用于修改显著性图内受病变影响的区域，而DDIM保证在显著性图外的正常解剖结构的重建。这两部分在每一步都进行融合，以确保生成的样本具有一致的外观，并在编辑和未编辑部分之间实现无缝过渡。我们验证了当我们的方法应用于健康样本时，输入图像在没有显著修改的情况下被重建。我们在脑病变分割任务中与替代的弱监督方法进行了比较，在所考虑的模型中获得了最高的平均Dice和IoU分数。

关键词

异常图，反事实示例，扩散模型，分割掩码

I. 引言

先进成像技术的显著进步显著提高了患者的医疗质量。这些尖端工具使放射科医生能够在诊断可疑区域（如肿瘤、息肉和血管破裂区域）时达到越来越高的准确性[46]。此外，医生现在能够实施精确且经过仔细测量的治疗方法，这得益于这些成像技术提供的宝贵支持。事实上，医学图像中病理标志物的检测在疾病诊断和进展监测中起着重要作用。然而，在许多情况下，感兴趣区域（ROI）的分割是由放射科医生手动进行的，这不仅是一个昂贵的过程，而且容易出错，并且在不同注释者之间存在不一致性[3, 47]。因此，开发自动化的ROI检测系统是一个非常活跃的研究领域，因为它具有节省时间和成本的潜力，同时减轻了与人工评估相关的一些固有偏差。

当患者被诊断为脑肿瘤时，病理区域的分割对于规划手术治疗、监测肿瘤的生长以及图像引导干预非常重要[12]。特别是，磁共振成像（MRI）是一种广泛使用的非侵入性技术，可以生成多种组织对比度。医学专家已广泛使用它来诊断脑肿瘤。然而，肿瘤可能会严重扭曲正常解剖结构，使得规划避免关键结构的手术方法变得更加困难。因此，生成等效的健康图像可以通过帮助识别解剖区域来改善手术规划。

另一个临床应用中，病变体积的检测在卒中管理中起着重要作用。特别是在预后决策、急性治疗选择过程[14]以及预测并发症[13]中非常重要。通常使用计算机断层扫描灌注（CTP）、灌注加权成像（PWI）或MRI扩散加权成像（DWI）来估计风险组织和缺血核心[15]。还开发了自动从灌注成像中计算这些估计的软件包，以促进卒中治疗的临床决策[16]。然而，计算机断层扫描（CT）是卒中成像中最常用的工具，因为它价格低廉、效率高且广泛可用[16]。因此，从CT扫描中定量测量梗死迹象虽然在灌注图像上更难执行，但在临床实践中将非常有帮助。

基于这些原因，我们提出了一种弱监督方法，能够自动分割MRI图像中的脑肿瘤和CT扫描中的卒中病变。特别是，我们生成异常图时不使用像素级注释，而是仅使用图像级标签（仅在训练时需要）。同样的方法也可以应用于医学图像中的其他像素级异常检测任务。

放射科医生对机器学习工具的看法从接受和热情到怀疑不一[18]。提供简单的异常图可能会被高度训练的放射科医生负面接受，他们可能认为这贬低了他们的专业知识[17]。因此，在我们的方法中，我们从病理图像中移除病变，并基于原始图像与其正常外观版本之间的差异生成异常图。健康版本的图像可以代替或补充异常图，以更好地与临床医生互动，并允许他们使用自己的推理来检测异常。事实上，放射科医生通常通过从正常图像的心理表征中检测偏差来发现异常[20]。了解自动图像分割工具的内部工作原理也可以增加临床医生对模型的信任[41]。此外，比较正常和异常图像是培训放射科医生的常见做法[19]。由于正常解剖结构可能差异很大，因此培训人员需要接触大量健康图像[18]。然而，大多数教学文件偏向于病理样本[21]。因此，通过将异常示例转换为匹配正常解剖结构，我们可以防止这种数据不平衡，并帮助更有效地培训放射科医生。

先前的工作使用了在健康样本上训练的自编码器[5, 6, 7]或GAN[8, 9, 27]将病变图像映射到其相应的正常版本。然而，自编码器并不总是生成清晰的图像，并且不能保证正确映射到健康版本。另一方面，GAN训练有时不稳定，依赖于许多超参数，并生成较差的样本[22]。因此，我们的方法基于扩散模型，这是一类生成模型，最近由于其在计算机视觉领域的卓越能力而受到欢迎。它们已被证明在样本质量上优于之前的最先进GAN[4]。

在[10]中，作者使用扩散模型和分类器引导[4]来恢复正常解剖结构。然而，引导采样过程所需的梯度必须从在噪声样本上训练的分类器中计算。该分类器通常产生不可靠的预测，因为在医学成像中，样本的类别通常由小细节决定，这些细节可能在仅经过几次噪声步骤后就会丢失。因此，使用这种方法，我们不能保证保留样本的原始结构，并且正常组织的许多细节可能会被修改。

最近的一项研究[39]引入了对抗性反事实注意力（ACAT），这是一种将病变图像映射到其健康对应物并识别感兴趣区域（ROI）的方法。特别是，为了生成反事实示例，作者使用了一个自编码器和一个单独训练的分类器来分别重建和分类图像。具体来说，他们确定了自编码器潜在空间中的最小偏移，该偏移将输入图像过渡到由分类器输出确定的所需目标类别。作者广泛比较了各种反事实和基于梯度的方法，用于生成归因图以识别脑和肺CT扫描中的疾病。他们证明了他们的方法在定位脑CT扫描中六个潜在区域的病变位置方面得分最高。此外，它在肺CT扫描上获得了最佳的IoU和Dice分数。

III. 方法

ACAT解决了潜在偏移方法在生成归因图方面的局限性；然而，通过ACAT获得的反事实示例并不完全令人满意。换句话说，ACAT能够识别图像中需要修改的区域，但不能准确说明如何修改以获得可信的反事实。这种限制是可以理解的，因为他们的论文的主要重点是将这些显著性图用于分类管道，而不是生成精确的反事实。

在我们的工作中，我们旨在通过提出一种两步方法来解决这一挑战。首先，我们使用ACAT获得初始显著性图，这些图提供了需要修改区域的粗略识别。然后，我们引入了一种新颖的扩散模型采样技术，该技术允许对这些区域进行有针对性的修改，同时保留图像的其余部分不变。通过在每一步融合这两个组件，我们实现了编辑和未编辑部分之间的无缝过渡，从而产生了一个现实的输出。通过考虑反事实示例与原始图像之间的差异，我们还可以获得最终的异常图。

我们观察到，我们的采样方法不仅生成了高度现实的反事实，还增强了使用ACAT在第一步中获得的初始显著性图。这是可能的，因为所选区域可能不会完全被扩散模型修改，从而保留了初始归因图中识别的健康解剖特征。图1展示了我们方法的视觉表示。

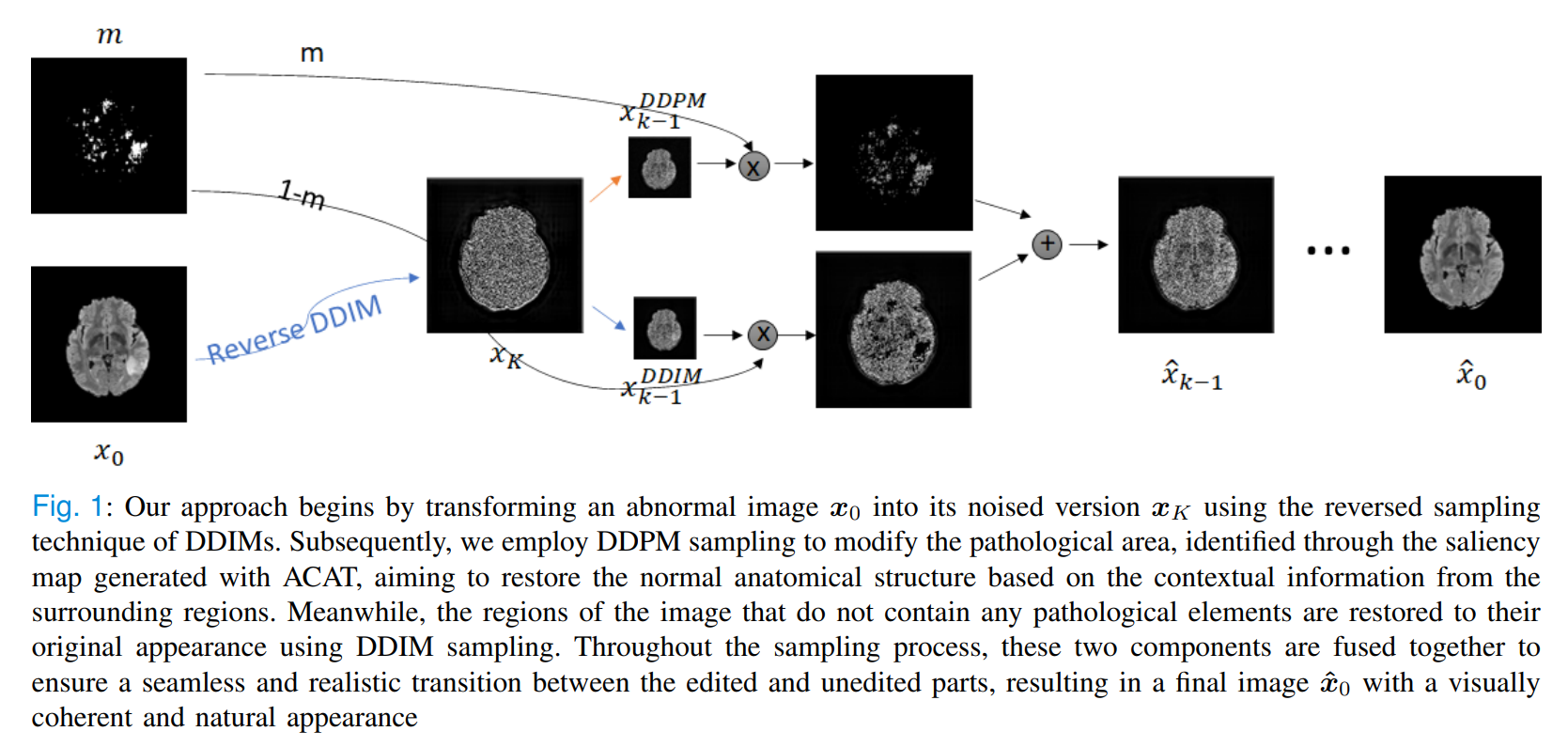
在接下来的部分中，我们首先简要概述扩散模型，然后介绍我们的采样技术，以生成可信的反事实并获取医学图像中病理区域的像素级异常图。

A. 扩散模型

扩散模型由前向过程定义，该过程从${\mathbf{x}}_0\sim q({\mathbf{x}}_0)$开始，逐步向数据添加噪声，经过$T$个时间步[1]：

$$q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)=\prod _{t=1}^{T}q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})$$

其中$q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})=\mathcal{N}({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I})$，以及后向过程：$p_{\theta }({\mathbf{x}}_0)=\int p_{\theta }({\mathbf{x}}_{0:T})d{\mathbf{x}}_{1:T}$，其中：

$$p_{\theta }({\mathbf{x}}_{0:T})=p({\mathbf{x}}_T)\prod _{t=1}^T{p}_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t),$$

$$p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)=\mathcal{N}({\mathbf{x}}_{t-1};{\mathbf{\mu }}_{\theta }({\mathbf{x}}_t,t),{\mathbf{\Sigma }}_{\theta }({\mathbf{x}}_t,t))$$

前向过程的参数${\beta }_t$设置为使${\mathbf{x}}_T$近似服从标准正态分布，因此$p({\mathbf{x}}_T)$也设置为标准正态先验。我们可以通过优化证据下界（ELBO）来训练后向过程以匹配前向过程的分布：$-L_{\theta }({\mathbf{x}}_0)\le log(p_{\theta }({\mathbf{x}}_0))$：

$$L_{\theta }({\mathbf{x}}_0)={\mathbb{E}}_q[L_T({\mathbf{x}}_0)+\sum _{t>1}{D}_{KL}(q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)||p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t))-log{p}_{\theta }({\mathbf{x}}_0|{\mathbf{x}}_1)]$$

其中$L_T({\mathbf{x}}_0)=D_{KL}(q({\mathbf{x}}_T|{\mathbf{x}}_0)||p({\mathbf{x}}_T))$。

前向过程的后验$q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)$和边缘$q({\mathbf{x}}_t|{\mathbf{x}}_0)$是高斯分布，KL散度可以以闭式形式计算。因此，扩散模型可以通过在(3)的随机项上采取随机梯度下降步骤来训练。如[1]所述，(1)中定义的噪声过程允许我们采样任意步骤的潜在变量，条件是$x_0$。设${\alpha }_t:=1-{\beta }_t$和${\hat{\alpha }}_t:={\prod }_{s=0}^t{\alpha }_s$，我们可以写：

$$q({\mathbf{x}}_t|{\mathbf{x}}_0)=\mathcal{N}({\mathbf{x}}_t;\sqrt{{\alpha }_t}{\mathbf{x}}_0,(1-{\hat{\alpha }}_t)\mathbf{I}).$$

因此：

$${\mathbf{x}}_t=\sqrt{{\alpha }_t}{\mathbf{x}}_0+\sqrt{(1-{\hat{\alpha }}_t)}\mathbf{ϵ},$$

其中$\mathbf{ϵ}\sim \mathcal{N}(0,\mathbf{I})$。

有许多方法可以参数化${\mathbf{\mu }}_{\theta }({\mathbf{x}}_t,t)$(2)在先验中。例如，我们可以使用神经网络预测${\mathbf{\mu }}_{\theta }({\mathbf{x}}_t,t)$。或者，我们可以预测${\mathbf{x}}_0$并使用它来计算${\mathbf{\mu }}_{\theta }({\mathbf{x}}_t,t)$。网络也可以用于预测噪声$\mathbf{ϵ}$。在[1]中，作者发现这种选择产生了最佳的样本质量，并引入了重新加权的损失函数：

$$L_{\text{simple}}={\mathbb{E}}_{t,{\mathbf{x}}_0,ϵ}[\Vert \mathbf{ϵ}-{\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t){\Vert }^2]$$

在训练扩散模型后，给定从$\mathcal{N}(0,\mathbf{I})$采样的${\mathbf{X}}_T$，我们可以通过递归应用采样方案生成新样本${\mathbf{x}}_0$：

$${\mathbf{x}}_{t-1}=\sqrt{{\hat{\alpha }}_{t-1}}\left(\frac{{\mathbf{x}}_t-\sqrt{(1-{\hat{\alpha }}_t){\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)}}{\sqrt{{\hat{\alpha }}_t}}\right)+\sqrt{1-{\hat{\alpha }}_{t-1}-{\sigma }_t^2}{\mathbf{ϵ}}_{\theta }({\mathbf{x}}_t,t)+{\sigma }_t\mathbf{ϵ}$$

在DDPM中：

$${\sigma }_t=\sqrt{(1-{\hat{\alpha }}_{t-1})/(1-{\hat{\alpha }}_t)}\sqrt{1-{\hat{\alpha }}_t/{\hat{\alpha }}_{t-1}}.$$

在DDIM中，通过设置${\sigma }_t=0$去除随机分量，采样过程变为确定性。

B. Dif-fuse

在我们的方法中，我们使用在健康样本上训练的DDPM和从对抗性生成的反事实示例中获得的显著性图，如ACAT[39]所示。我们选择ACAT是因为它在识别脑和肺CT扫描中的病理区域方面表现出色。然而，原则上，显著性图也可以使用任何其他方法生成。给定一个病变图像${\mathbf{x}}_0$，我们首先选择一个噪声量$K\in [0,T]$，并使用[2]中提出的逆DDIM采样方案将图像映射到其噪声版本${\mathbf{x}}_K$：

$${\mathbf{x}}_{t+1}={\mathbf{x}}_t+\sqrt{{\hat{\alpha }}_{t+1}}\left[\left(\sqrt{\frac{1}{{\hat{\alpha }}_t}}-\sqrt{\frac{1}{{\hat{\alpha }}_{t+1}}}\right){\mathbf{x}}_t+\left(\sqrt{\frac{1}{{\hat{\alpha }}_{t+1}}-1}-\sqrt{\frac{1}{{\hat{\alpha }}_t}-1}\right){ϵ}_0({\mathbf{x}}_t,t)\right]$$

然后，我们使用大小为$5\times 5$的高斯核平滑显著性图，以获得更均匀且孤立像素较少的掩码$\mathbf{m}$。我们使用DDPM采样编辑掩码内的病变区域。由于扩散模型是在正常样本上训练的，这些区域被映射到健康外观。解剖结构的其余部分需要保留，因此我们使用DDIM采样来处理掩码外的区域，如(7)所示，${\sigma }_t=0$。为了获得一致的结果，我们在每个采样步骤中将掩码部分与图像的其余部分混合。换句话说，给定${\hat{\mathbf{x}}}_t$，我们计算：

$${\hat{\mathbf{x}}}_{t-1}={\mathbf{x}}_{t-1}^{DDPM}\odot \mathbf{m}+{\mathbf{x}}_{t-1}^{DDIM}\odot (1-\mathbf{m})$$

其中$\odot$是Hadamard积。通过这种方式，编辑过程集中在显著性图捕获的部分，防止对扫描的结构特征进行随机更改。事实上，DDIM采样保证了不需要编辑的部分的重建。此外，病理部分的更改由DDPM考虑周围的解剖结构进行。我们的方法总结在算法1中。

当使用(9)计算${\hat{\mathbf{x}}}_{t-1}$时，两个组件的总和可能不会产生完全一致的结果。然而，这种不一致性在下一个扩散步骤中得到解决，该步骤更好地融合了两个组件。如果我们简单地使用DDPM计算${\hat{\mathbf{x}}}_0$，然后在采样过程结束时仅应用掩码，则不会出现这种情况。图3展示了这种效果的图示，我们可以观察到，仅在采样过程结束时应用掩码生成的正常图像（b）表现出一些伪影，并且在编辑和未编辑区域之间缺乏无缝过渡。

通过这种方式，我们能够获得给定病理图像的正常版本。为了获得异常图，我们首先计算原始图像与生成图像之间的差异，然后对结果图应用大小为$5\times 5$的核进行腐蚀和膨胀，以去除噪声，最后使用相同的核进行膨胀和腐蚀，以关闭图中的小孔。

C. 训练细节

扩散模型训练了60,000次迭代，批量大小为10，使用[11]中提出的损失和AdamW优化器，学习率为1e-4，${\beta }_1=0.9$，${\beta }_2=0.999$，权重衰减系数为0.05。我们使用了EMA率为0.99，噪声调度如[1]中所述，将前向过程方差设置为从第一步的$10^{-4}$线性增加到最后一步的0.02。训练在一台NVIDIA A100 GPU上大约需要两天时间。我们使用了1000个采样步骤和一个U-Net架构，第一层有128个通道，分辨率为8,16,32的注意力头。U-Net模型使用了一系列残差层和下采样卷积，然后是另一系列残差层和上采样卷积。这些层通过跳过连接连接，连接具有相同空间大小的层。特别是，我们每个分辨率使用了两个残差块。

IV. 实验

A. 数据

我们在IST-3[24]、BraTS 2021[25]和白质高信号（WMH）[49]数据集上进行了实验。

IST-3是一项随机对照试验，收集了3035名出现卒中症状的患者的脑成像数据，主要是CT扫描。扫描在两个时间点进行：患者入院后立即进行，然后在24-48小时后再次进行。参与试验的放射科医生评估了早期缺血迹象的存在与否，并记录了阳性扫描中任何识别到的病变位置。在我们的分析中，我们总共考虑了5681次扫描，其中46.31%被分类为阴性（无病变），其余扫描为阳性。特别是，我们考虑了每次扫描的11个切片，并将每个切片调整为256×256。有关试验协议、数据收集和数据使用协议的更多详细信息，请参阅以下URL：IST-3信息[1]。

BraTS 2021包括为脑肿瘤分割（BraTS）挑战收集的数据。该数据集由术前基线多参数磁共振成像（mpMRI）扫描组成，使用不同的临床协议和各种扫描仪从多个机构获得。该挑战的主要目标是评估和比较在mpMRI扫描中分割不同亚区域的高度异质性脑胶质母细胞瘤的先进技术。它包括四种模态的扫描（FLAIR、T1、T1加权和T2）。特别是，我们考虑了公开可用的BraTS 2021训练数据集，包含1251名患者的扫描。每次扫描有155个切片。然而，我们移除了顶部和底部的25个切片，因为它们的内容最少，并且在将剩余的切片零填充到256×256（从原始尺寸240×240）之前，移除了任何其他空切片。最终，我们剩下131,164个切片，其中79,113个为阳性。有关数据集的更多信息，请参阅：BraTS 2021信息[2]。

WMH是为白质高信号分割挑战收集的。我们使用了测试集中的数据，该数据集由来自五个MR扫描仪的110次扫描组成，包括FLAIR和T1模态。我们将每个切片中心裁剪并调整为256×256。

由于IST-3中没有病变注释，我们使用该数据集来评估生成图像的质量，而不是分割准确性。另一方面，对于BraTS 2021和WMH数据集，我们可以访问病变注释，从而能够对我们创建的异常图进行定量分析。IST-3和BraTS 2021被分为训练集、验证集和测试集，比例为70-15-15。在WMH上，我们评估了在BraTS 2021上训练的模型，没有进一步微调，以测试它们的跨域泛化能力。

B. 实验设置

我们将我们的方法与使用自编码器、GAN和扩散模型的竞争性弱监督方法进行了比较。特别是，我们考虑了DenoisingAE[50]，遵循官方仓库[3]的实现，f-Ano GAN[23]，其中我们训练了WGAN和izi编码器各500,000次迭代，使用分类器引导（CG）的扩散模型，遵循[10]的实现，噪声水平$K=500$和梯度比例$s=100$，无分类器引导（CFG）[26]引导比例$s^{\prime }=3$（在我们的实验中获得了最佳结果）。此外，我们还评估了AnoDDPM[51][4]和AutoDDPM[52][5]。对于前者，我们在验证数据上观察到使用100个噪声步骤获得了最佳结果，而对于后者，我们遵循[52]的超参数，并设置掩码阈值以获得最多5%的误报，同时在验证数据上调整最终的异常二值化阈值（最佳阈值被发现为0.1）。作为消融实验，我们还考虑了直接使用ACAT获得的显著性图作为异常图的结果，如我们的方法中所阈值化的，以及不同的DDIM和DDPM采样组合用于前向和后向采样过程（无掩码）。特别是，我们考虑了从扩散模型的前向过程噪声图像进行DDPM采样（在实验中称为DDPM），从DDIM反演噪声图像进行DDPM采样（DDIM-DDPM），从扩散模型的前向过程噪声图像进行DDIM采样（DDPM-DDIM），以及从DDIM反演噪声图像进行DDIM采样（DDIM）。

为了将BraTS 2021中的四种MRI模态作为模型的输入，我们将它们在通道维度上进行了连接。

C. 反事实示例

在图2和4中，我们展示了使用不同方法获得的健康图像和异常图的示例。我们可以观察到，f-Ano GAN无法生成可信的反事实，通常生成的图像质量较差且外观不真实。另一方面，其他方法能够生成更高质量的结果。

然而，使用DenoisingAE、AnoDDPM和AutoDDPM获得的结果中，病理病变仍然部分可见，而使用CG和CFG获得的反事实似乎存在一些伪影，这不仅可能影响反事实示例的真实性，还可能影响从它们获得的异常图的精度。为了更好地量化这些方法在准确分割病理区域方面的能力，我们计算了它们生成的异常图的Dice和IoU分数。

我们还在健康样本上测试了我们的方法。理想情况下，我们希望我们的生成过程在给定正常图像作为输入时充当恒等函数。图6展示了一些示例，我们可以观察到，我们的采样技术引入的变化相对较小，Dif-fuse保留了图像的结构和整体外观。

D. 超参数

在早期实验中，我们观察到，当使用显著性图生成Dif-fuse中所需的掩码时，对其进行二值化会产生更好的结果。因此，在验证集上，我们探索了显著性图二值化的最佳阈值水平以及在我们扩散模型采样期间使用的最合适的噪声量。

在图5中，我们绘制了不同超参数值获得的Dice分数。正如我们所观察到的，当使用500个噪声步骤并选择显著性图中第90百分位的像素时，我们获得了最佳性能。在图7中，我们展示了使用不同噪声水平获得的反事实。我们可以观察到，较小的噪声参数值不允许扩散模型对图像进行足够的修改，而较大的值会引入影响生成图像质量的伪影，从而也影响了相应异常图的Dice分数。

E. 定量评估

我们在BraTS 2021和WMH上评估了使用不同方法获得的异常图。结果显示在表I中。我们可以观察到，我们的方法在WMH上获得了最佳性能（平均Dice和IoU分别为0.569和0.526），在BraTS 2021上获得了0.699的Dice和0.620的IoU（DenoisingAE在BraTS 2021上排名第二，Dice和IoU分别为0.681和0.614，ACAT在WMH上排名第二，Dice为0.530，IoU为0.497）。

对作为我们方法一部分的ACAT获得的显著性图的消融实验显示，如Dif-fuse中那样从扩散模型采样对于获得最佳结果和提高显著性图的病变检测能力至关重要。此外，对前向和后向采样的不同DDPM和DDIM组合的消融实验表明，我们的方法中引入的每一步结合两者以及掩码引导对于实现最佳结果非常重要。我们还在BraTS 2021上使用Grad-CAM[33]和梯度方法[32]获得的显著性掩码对我们的方法进行了消融实验，以引导扩散模型的采样。特别是，使用前一种方法，我们获得了平均Dice为0.539和平均IoU为0.512，而使用后一种方法获得了0.576和0.533。正如预期的那样，由于这些显著性图的质量较低，结果不如使用ACAT获得的掩码（Dice：0.699，IoU：0.620）好，这与ACAT中的发现一致。

表I中还显示了在IST-3上获得的KID分数，将生成的正常图像与数据集中的真实阴性图像进行比较。我们选择此指标是因为它减少了Fréchet Inception Distance[55]中固有的偏差，特别是在处理少量样本时。我们使用Inception v3模型的最后一个卷积层的特征计算它。我们可以观察到，DDIM反演后接DDPM采样的消融实验在IST3上获得了最佳KID（0.037），其次是DDPM（0.039）和Dif-fuse（0.040）。这可以解释为，如消融实验中那样无约束采样（无掩码）可以获得更真实的图像。然而，它也有修改样本整体解剖结构的缺点，导致异常图的分割效果较差。

为了为我们的结果提供背景，重要的是考虑最先进的监督分割方法的性能。在BraTS2021测试数据上，最佳监督方法[6]在“增强肿瘤”（ET）、“肿瘤核心”（TC）和“整个肿瘤”（WT）类别上分别获得了0.837、0.877和0.925的Dice分数。对于WMH数据，表现最佳的监督方法获得了0.81的Dice分数[7]。虽然我们的方法尚未匹配这些监督结果，但它展示了在没有注释的情况下具有竞争力的性能。这突显了生成方法在医学图像分析中的潜力，特别是在注释数据稀缺或获取成本高的情况下。

F. 与修复方法的比较

虽然我们提出的方法与修复技术有相似之处，但有两个关键区别。1）与传统的修复不同，传统修复假设要修改的区域有预定义的掩码，我们的方法解决了自动识别目标区域的挑战，包括考虑固有的位置不确定性。2）修复通常涉及仅使用上下文线索完成完全缺失的部分。相比之下，我们的方法利用了现有的病理特征，我们旨在将其呈现为健康组织。这些差异需要一种更细致的方法，将修复元素与专门用于医学图像分析和转换的技术相结合。

作为修复方法的代表，我们测试了Repair[56]，使用ACAT获得的掩码（因为原始方法假设有要修复区域的地面实况掩码）。我们使用了250个时间步，跳跃大小为10的10次重采样，如[56]中推荐的那样。我们在BraTS2021上获得了Dice分数为0.649和IoU为0.575，在WMH上获得了Dice为0.532和IoU为0.484。

值得注意的是，修复方法在我们的设置中可能会遇到困难，因为它们不是设计用来利用掩码区域中的现有信息或处理要修复区域的不确定性。

V. 结论

在本研究中，我们提出了一种通过扩散模型从病理图像中移除病变的方法，以生成可信的反事实并生成异常图。为了实现这一目标，我们采用了一种两步方法。首先，我们使用ACAT生成初始显著性图。这些图提供了需要修改区域的初步近似。接下来，我们引入了一种新颖的扩散模型采样方法。该技术使我们能够对识别出的区域进行有针对性的修改，同时保留图像的其余部分。我们在每一步融合这两个组件，以确保编辑和未编辑部分之间的平滑过渡和现实的输出。特别是，我们使用DDPM采样修复ROI，并使用DDIM重建正常解剖结构。通过对反事实示例与原始图像之间的差异应用一些后处理步骤，我们还可以获得最终的异常图。

我们观察到，我们的采样方法不仅生成了高度现实的反事实图像，还增强了ACAT在第一步中生成的初始显著性图。特别是，我们在BraTS 2021和WMH上获得了所有考虑方法中最高的平均Dice和IoU分数，同时在IST-3上获得了较低但可比的KID，与无约束（无掩码）扩散采样方法相比。我们的模型展示了在具有视觉相似病理的数据集（BraTS2021和WMH）上的有希望的泛化能力。这种跨数据集性能表明其具有更广泛的适用性。然而，我们承认，我们的方法的泛化能力的全面评估，特别是对罕见或未见过的疾病的泛化能力，值得进一步探索。用于计算初始显著性图的二元分类器在这方面是一个关键组件。为了增强模型的通用性，未来的工作可以专注于在更多样化的病理上训练该分类器。这将揭示并可能提高模型识别和处理更广泛异常的能力，从而扩展其适用性。我们将我们的方法应用于脑部的MRI和CT扫描，但我们相信它也可以应用于许多其他需要图像分割的医学成像应用中。我们留待未来工作进一步测试。

声明

本文内容为论文学习收获分享，受限于知识能力，本文对原文的理解可能存在偏差，最终内容以原论文为准。本文信息旨在传播和学术交流，其内容由作者负责，不代表本号观点。文中作品文字、图片等如涉及内容、版权和其他问题，请及时与我们联系，我们将在第一时间回复并处理。