Lagrange对偶法

最新推荐文章于 2024-07-04 13:07:02 发布

zzz的学习笔记本

最新推荐文章于 2024-07-04 13:07:02 发布

阅读量812

点赞数 21

分类专栏：优化算法凸优化文章标签：凸优化

本文链接：https://blog.csdn.net/qq_42806204/article/details/135554028

版权

凸优化同时被 2 个专栏收录

3 篇文章 0 订阅

订阅专栏

优化算法

1 篇文章 0 订阅

订阅专栏

本文介绍了Lagrangian函数、拉格朗日乘子、拉格朗日对偶问题，探讨了强对偶性和斯莱特条件在凸优化中的作用，以及Karush-Kuhn-Tucker条件在满足强对偶性时的优化问题中的应用。

摘要由CSDN通过智能技术生成

这里写自定义目录标题

Lagrange dual
上海交通大学 CS257 Linear and Convex Optimization
南京大学 Duality (I) - NJU

the standard form (5.1)
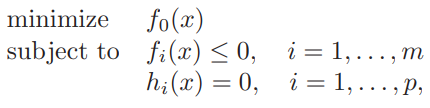
在这里插入图片描述
$\begin{array}{l} {\mathop {\min }_{\bf{X}} \;\;f\left( {\bf{X}} \right)}\\ {{\rm{s}}.{\rm{t}}.\;{g_i}\left( {\bf{X}} \right) \le 0,\forall i = 1, \ldots ,m,} \end{array}$

5.1.1 The Lagrangian

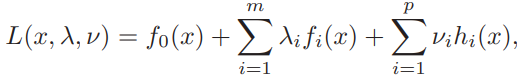
在这里插入图片描述
the dual variables or Lagrange multiplier vectors associated with the problem (5.1).

5.1.2 The Lagrange dual function

the minimum value of the Lagrangian
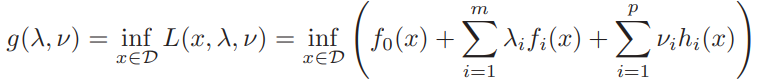
在这里插入图片描述

5.2 The Lagrange dual problem

the Lagrange dual problem associated with the problem (5.1).
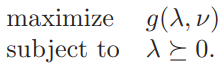
在这里插入图片描述

5.2.3 Strong duality and Slater’s constraint qualification

在这里插入图片描述

5.2.3 Strong duality and Slater’s constraint qualification

Slater’s theorem states that
strong duality holds, if Slater’s condition holds (and the problem is convex).
strong duality obtains, when the primal problem is convex and Slater’s condition holds

Slater’s Condition for Convex Problems
上海交通大学 CS257 Linear and Convex Optimization
在这里插入图片描述

5.5.3 KKT optimality conditions

Karush-Kuhn-Tucker (KKT) conditions
在这里插入图片描述
for any optimization problem with differentiable objective and constraint functions for which strong duality obtains, any pair of primal and dual optimal points must satisfy the KKT conditions (5.49).