本文概述了安全强化学习中的关键算法，如TrustRegionPolicyOptimization(TRPO),ConstrainedPolicyOptimization(CPO),Reward-CorrectedPolicyOptimization(RCPO),Projection-BasedCPO(PCPO),First-OrderConstraintOptimizationinPolicySpace(FOCOPS),PenalizedProximalPolicyOptimization(P3O),ConstraintRectifiedPolicyOptimization(CRPO)以及CUP。讨论了它们的数学原理、会议发表和开源实现，包括在gym和safety-gym等环境中应用。
这里写自定义目录标题
TRPO
如何看懂TRPO里所有的数学推导细节? - 小小何先生的回答 - 知乎
参考资料 Safe Reinforcement Learning
安全/约束强化学习路线图（Safe RL Roadmap）编辑于 2023-05-06
Safe RL 的一点点总结编辑于 2021-04-25
1.CPO
2.RCPO
3.CPPO-PID
4.SafeLayer+DDPG
5.Safety-Gym
【安全强化学习· 一】Safe Reinforcement Learning（一）2020
Constrained reinforcement learning
constrained markov decision processes
OpenAI/safety-starter-agents github
综述论文
J. García and F. Fernández, “A comprehensive survey on safe reinforcement learning,” J. Mach. Learn. Res., Aug. 2015.
Liu, Yongshuai, Avishai Halev, and Xin Liu. “Policy learning with constraints in model-free reinforcement learning: A survey.” The 30th international joint conference on artificial intelligence (IJCAI). 2021.
Shangding Gu; Long Yang; Yali Du; Guang Chen; Florian Walter; Jun Wang, “A Review of Safe Reinforcement Learning: Methods, Theories, and Applications,” in IEEE Transactions on Pattern Analysis and Machine Intelligence, Dec. 2024.
A Review of Safe Reinforcement Learning: Methods, Theory and Applications github
安全强化学习方法、理论与应用综述
Shangding Gu, Jakub Grudzien Kuba, Yuanpei Chen, Yali Du, Long Yang, Alois Knoll, and Yaodong Yang. Safe multi-agent reinforcement learning for multi-robot control. Artificial Intelligence, 2023.
NeurIPS 2023: Safe Policy Optimization: A benchmark repository for safe reinforcement learning algorithms
PKU-Alignment/Safe-Policy-Optimization
OmniSafe: An Infrastructure for Accelerating Safe Reinforcement Learning Research
PKU-MARL/OmniSafe github
PKU-MARL/OmniSafe
omnisafe算法
杨耀东团队
环境
Gymnasium
Safety-Gym
Alex Ray, Joshua Achiam, and Dario Amodei. Benchmarking safe exploration in deep reinforcement learning. arXiv preprint arXiv:1910.01708, 7(1):2, 2019.
safety-gym
safety-gym openai网页
TRPO Lagrangian and PPO Lagrangian
Benchmarking Safe Exploration in Deep Reinforcement Learning
Safety-Gymnasium
Jiaming Ji, Borong Zhang, Jiayi Zhou, Xuehai Pan, Weidong Huang, Ruiyang Sun, Yiran Geng, Yifan Zhong, Josef Dai, Yaodong Yang
“Safety gymnasium: A unified safe reinforcement learning benchmark.” Advances in Neural Information Processing Systems 36 (2023).
Safety-Gymnasium文档
safety-gymnasium文档
Safety-Gymnasium, a collection of environments specifically for SafeRL, built upon the Gymnasium and MuJoCo. Enhancing the extant Safety Gym framework
Figure 2: Upper: The Single-Agent Robots of Gymnasium-based Environments.
Lower: The Multi-Agent Robots of Gymnasium-based Environments.
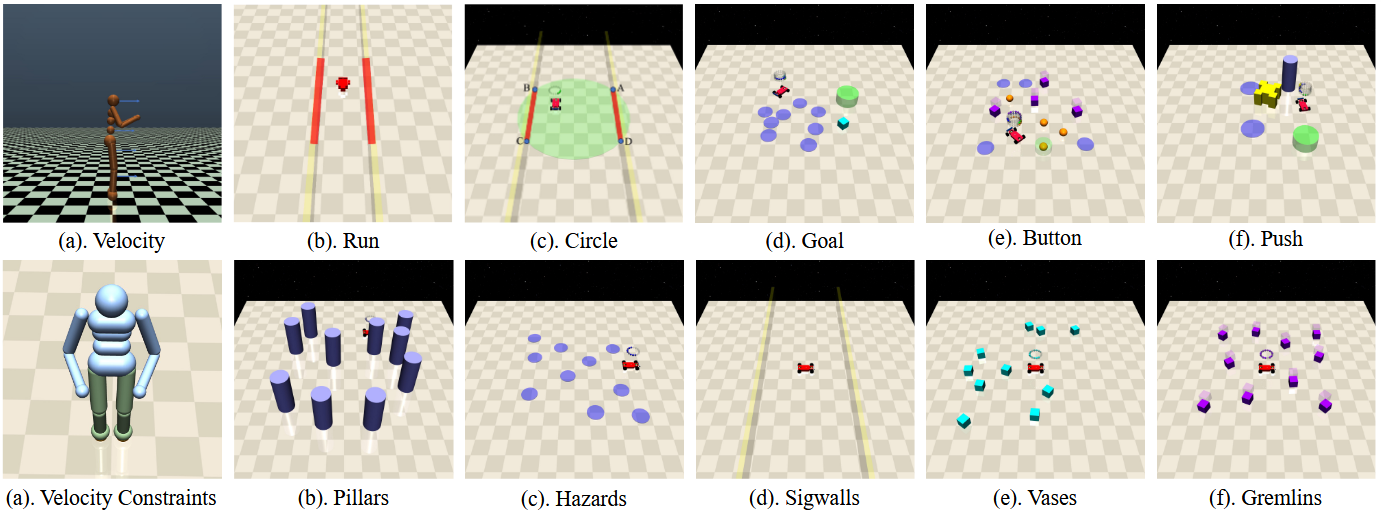
Figure 3: Upper: Tasks of Gymnasium-based Environments;
Lower: Constraints of Gymnasiumbased Environments.
Bullet-Safety-Gym
安装教程
Win 10、Win 11 安装 MuJoCo 及 mujoco-py 教程
日期：20240118
操作系统：Windows 10
python版本：3.8.18
mujoco版本：mjpro150
mujoco-py版本：1.50.1.0
gym版本：pip install gym==0.25.2
vs_buildtools_2017.exe
Cython.Compiler.Errors.CompileError: F:\Anaconda\envs\envpy38\lib\site-packages\mujoco_py-1.50.1.0-py3.8.egg\mujoco_py\cymj.pyx
pip install Cython==3.0.0a10
安全强化学习简介
算法
OmniSafe: An Infrastructure for Accelerating Safe Reinforcement Learning Research
omnisafe算法
On-Policy
| Algorithm | Type | Time | Conference | Citations | |
|---|---|---|---|---|---|
| CPO | 约束策略优化 | Convex Optimization 二阶 | 2017 | ICML | 1214 |
| RCPO | 奖励CPO | Primal Dual | 2018 | ICLR | 452 |
| PCPO | 基于投影的CPO | Convex Optimization 二阶 | 2019 | ICLR | 188 |
| FOCOPS | 策略空间中的一阶约束优化 | Convex Optimization 一阶 | 2020 | NIPS | 87 |
| CRPO | 约束修正策略优化 | Primal | 2021 | ICML | 84 |
| P3O | 惩罚PPO | Penalty Function | 2022 | IJCAI | 32 |
| CUP | 约束更新投影 | Convex Optimization 一阶 | 2022 | NIPS | 18 |
王雪松, 王荣荣, 程玉虎. 安全强化学习综述. 自动化学报, 2023, 49(9): 1813−1835 doi: 10.16383/j.aas.c220631
安全强化学习综述
2.2.2 信赖域法
约束型策略优化 (Constrained policy optimization, CPO)
基于投影的约束策略优化 (Projection-based constrained policy optimization, PCPO)
一阶约束优化方法 (First order constrained optimization in policy space, FOCOPS)
惩罚近端策略优化 (Penalized proximal policy optimization, P3O)
约束修正策略优化 (Constraint-rectified policy optimization, CRPO)
约束变分策略优化 (Constrained variational policy optimization, CVPO)
PPO-Lagrangian TRPO-Lagrangian 2019
Alex Ray, Joshua Achiam, and Dario Amodei. Benchmarking safe exploration in deep reinforcement learning. arXiv preprint arXiv:1910.01708, 7(1):2, 2019.
safety-gym
safety-gym openai网页
TRPO Lagrangian and PPO Lagrangian
Benchmarking Safe Exploration in Deep Reinforcement Learning
github代码
This repo contains the implementations of PPO, TRPO, PPO-Lagrangian, TRPO-Lagrangian, and CPO used to obtain the results in the “Benchmarking Safe Exploration” paper, as well as experimental implementations of SAC and SAC-Lagrangian not used in the paper.
omnisafe网页
omnisafe代码 PPO-Lagrangian
omnisafe代码 优化Lagrangian乘子
omnisafe代码 PPO
CPO 2017 ICML
CPO github
CPO omnisafe
知乎 南山张学有
Constrained Policy Optimization 上海交通大学 工学硕士
PCPO 2019 ICLR
PCPO omnisafe
FOCOPS 2020 NIPS
github代码
omnisafe代码
FOCOPS omnisafe
FOCOPS slideslive ★★★
FOCOPS slideslive 短
CPO的问题
从当前策略获取样本轨迹时产生的错误。
泰勒近似引起的近似误差。
使用共轭法计算Fisher信息矩阵的逆矩阵会产生近似误差。
FOCOPS的优势
实现简单，只使用一阶近似。
简单的一阶法避免了泰勒法和共轭法引起的误差。
在实验中表现优于CPO。
不需要任何恢复步骤。
Two-stage Policy Update
∇ ^ θ L π ( θ ) ≈ 1 B ∑ j = 1 B [ ∇ θ D K L ( π θ ∥ π θ ′ ) [ s j ] − 1 β ∇ θ π θ ( a j ∣ s j ) π θ ′ ( a j ∣ s j ) ( A ^ j − ν A ^ j C ) ] 1 D K L ( π θ ∥ π θ ′ ) [ s j ] ≤ δ \hat{\nabla}_\theta \mathcal{L}_\pi(\theta) \approx \frac{1}{B} \sum_{j=1}^B\left[\nabla_\theta D_{\mathrm{KL}}\left(\pi_\theta \| \pi_{\theta^{\prime}}\right)\left[s_j\right]-\frac{1}{\beta} \frac{\nabla_\theta \pi_\theta\left(a_j \mid s_j\right)}{\pi_{\theta^{\prime}}\left(a_j \mid s_j\right)}\left(\hat{A}_j-\nu \hat{A}_j^C\right)\right] \mathbf{1}_{D_{\mathrm{KL}}\left(\pi_\theta \| \pi_{\theta^{\prime}}\right)\left[s_j\right] \leq \delta} ∇^θLπ
最低0.47元/天 解锁文章
扫一扫
1639
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
