本文详细介绍了如何使用向量法将凹多边形转换为凸多边形，涉及判断凹点、延长边的相交测试、求交点以及广度优先分割等步骤，以进行更精确的碰撞检测。
在进行凹多边形碰撞检测的时候需要先将凹多边形转换为多个凸多边形，凸多边形再利用分离轴算法进行碰撞检测,这篇文章介绍利用向量法实现凹多边形转凸多边形的具体实现。算是碰撞检测的一个进阶话题，有刚需的朋友可以看看。
需要知道分离轴检测可以点传送门。
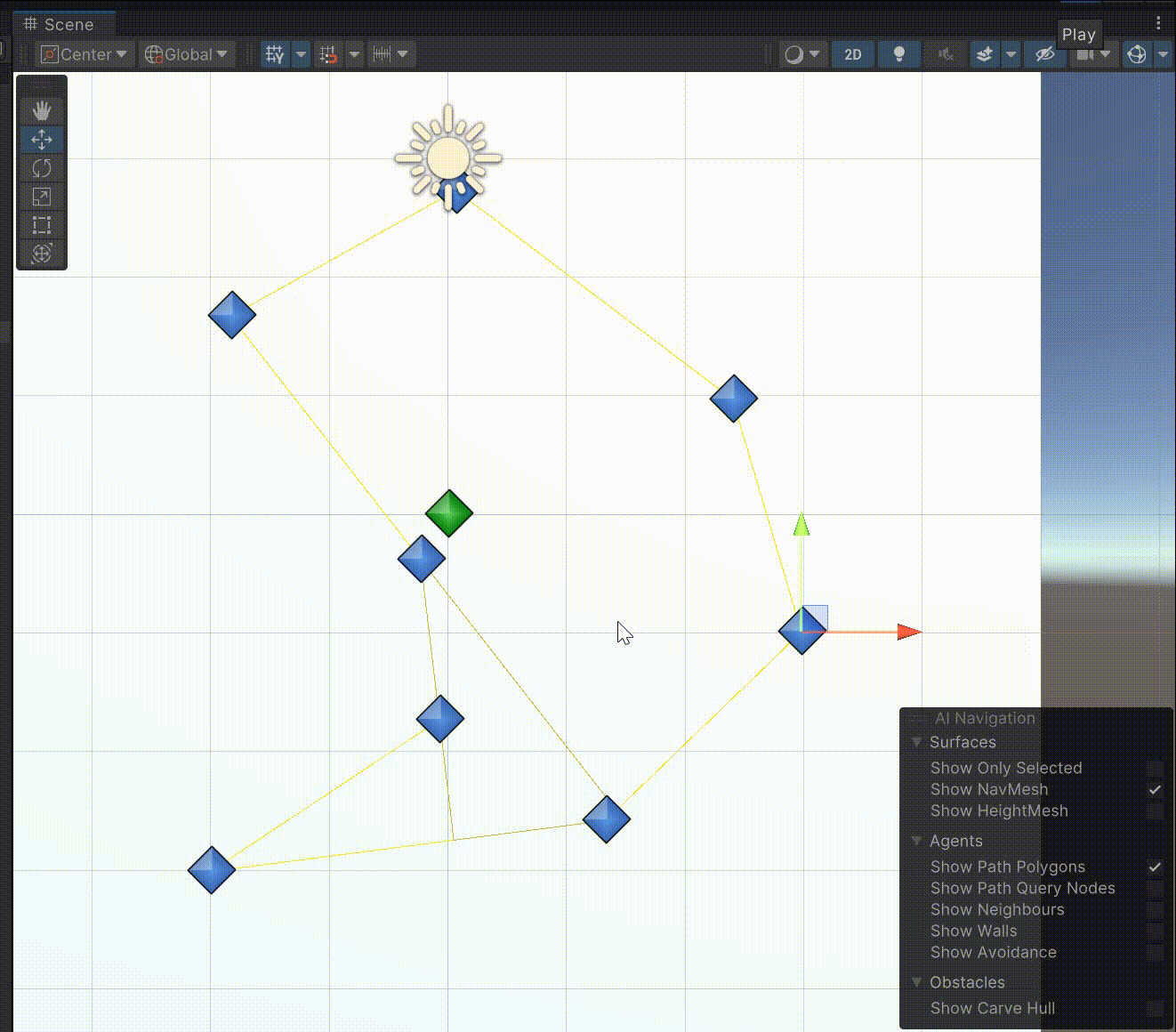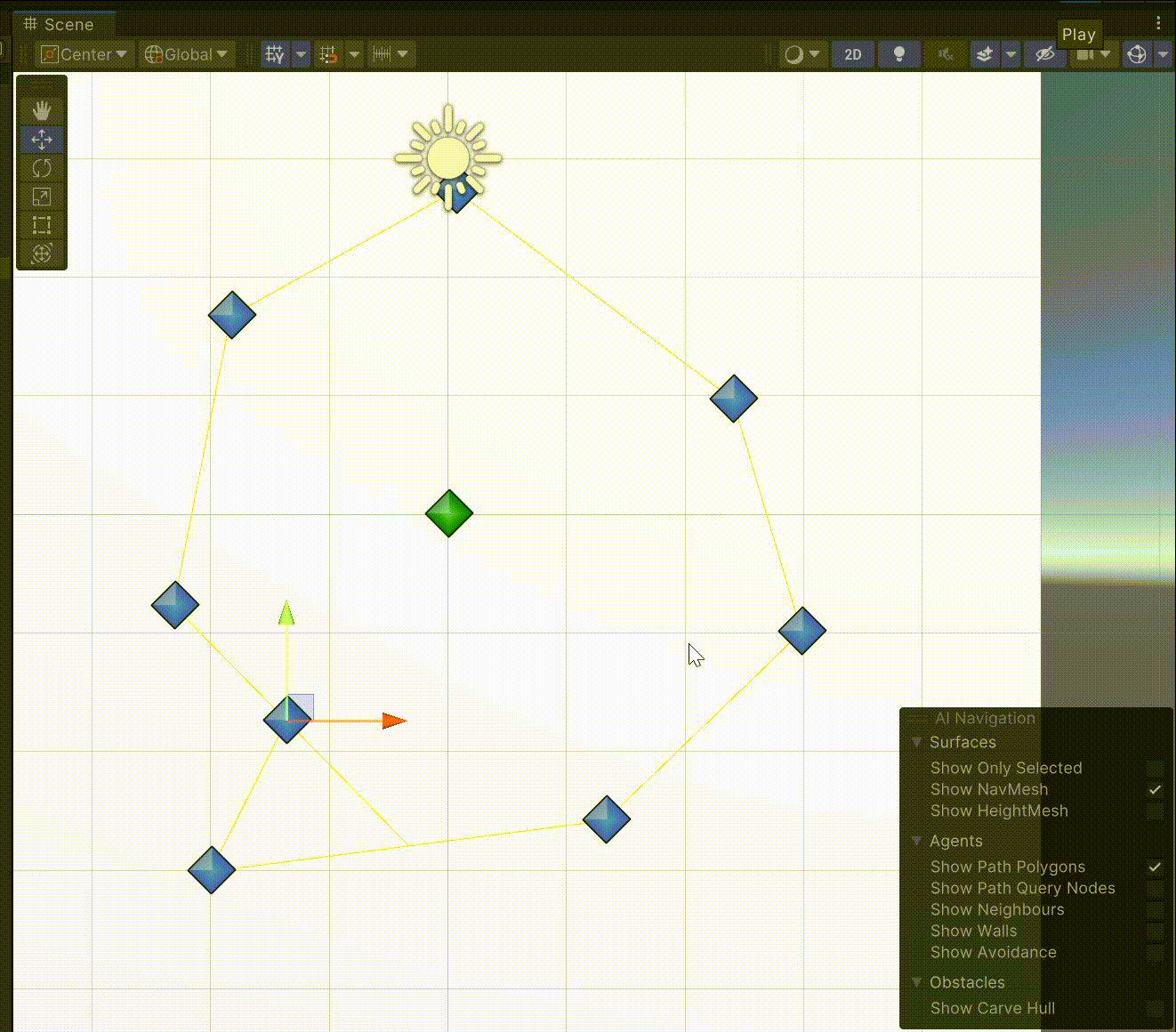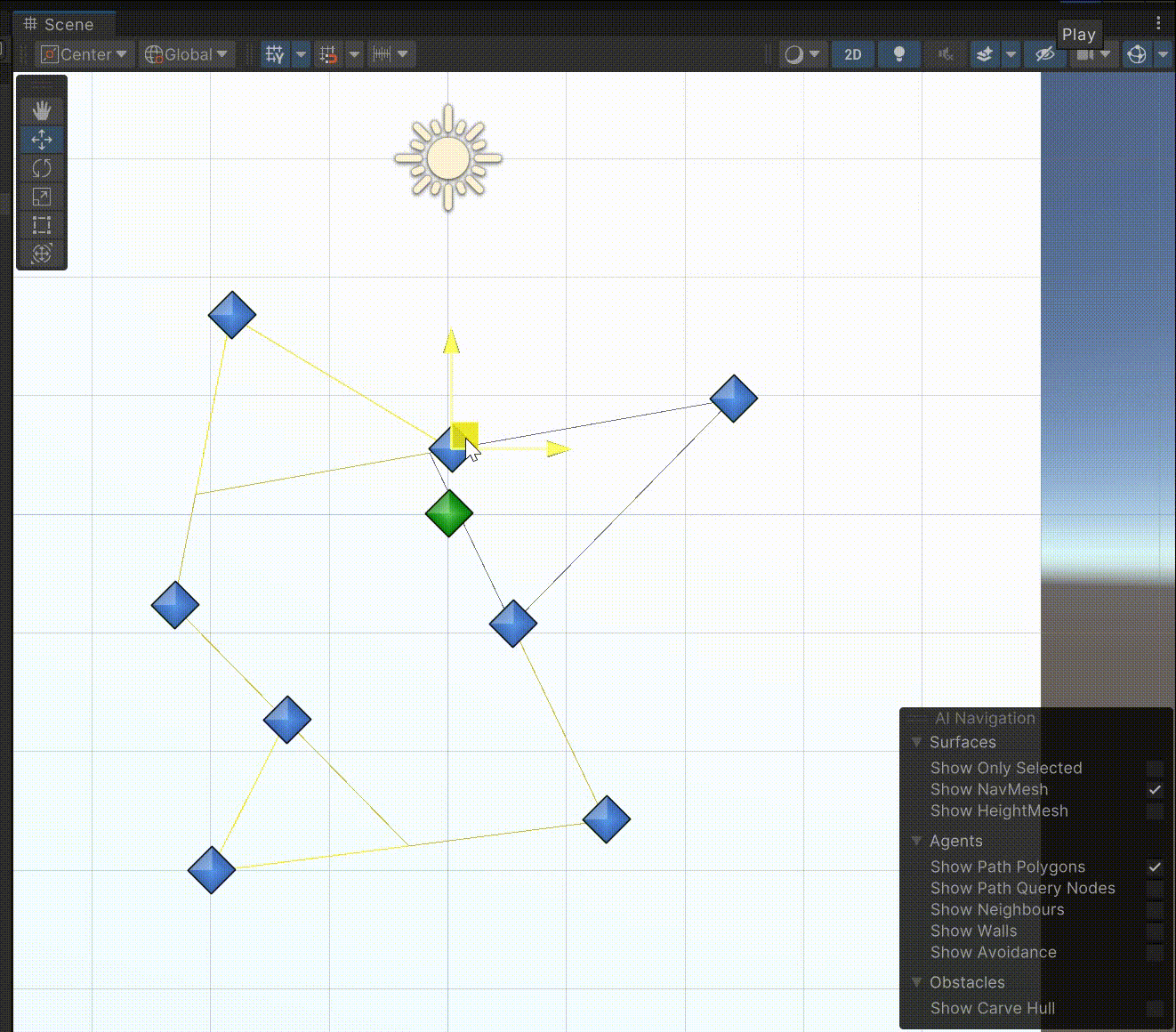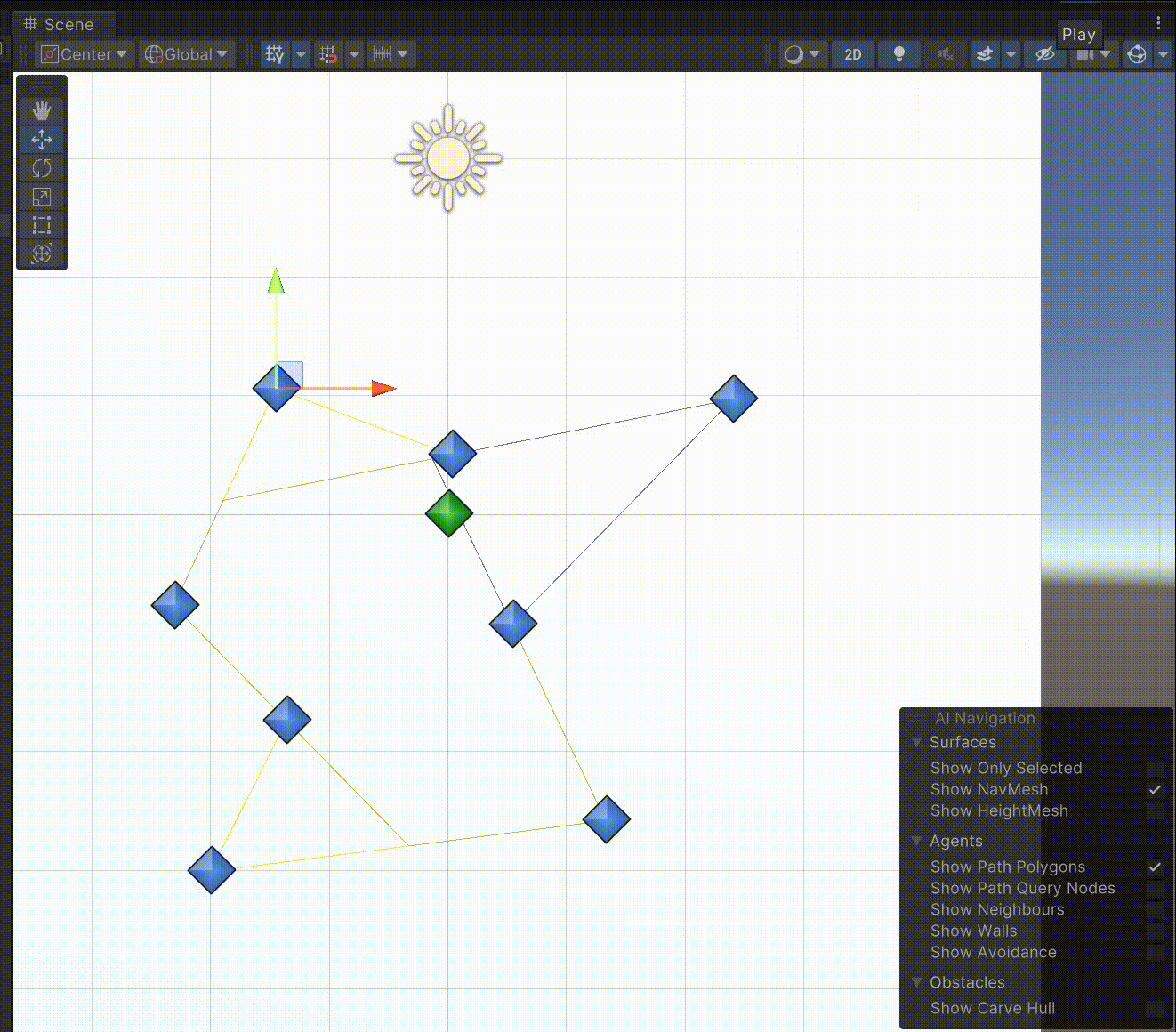
流程图
思路很简单，就是每次找一个凹点，切割一次除去一个凹点获得两个新的多边形，多边形继续切割直到所有多边形都是凸多边形为止。之所以叫向量法是因为判断凹点和延长边的时候都是利用向量来做。
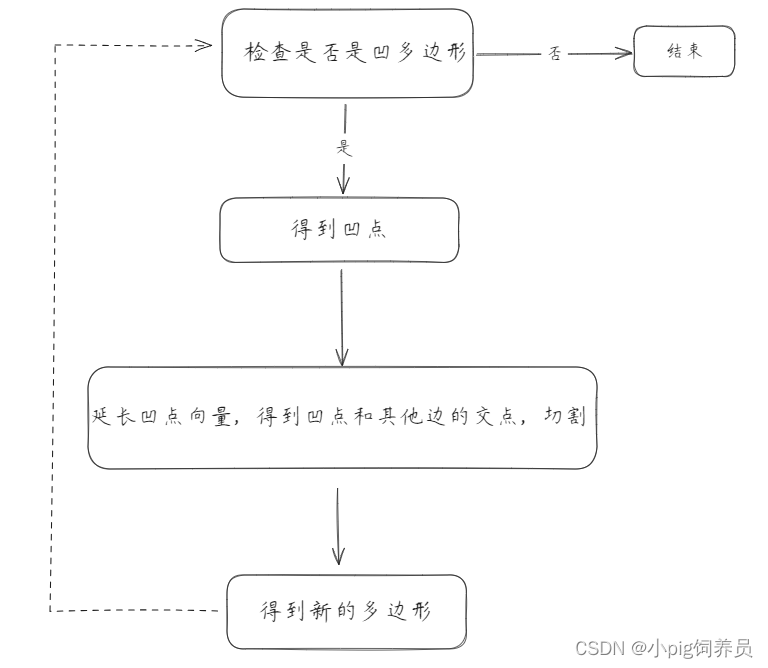
但是具体每个步骤的实现都是对初高中数学是否还记得的深刻考验(确信)
接下来具体解析每一个步骤，完整代码会放在文章最后。
检查是否是凹多边形
我们规定多边形的点的顺序是逆时针存储，检查是否是凹多边形即检查某个点的内角是否大于180度。
unity是左手系，大于180度的内角所在两条边叉乘所得方向是向外的，我们逆时针遍历每个边两两之间依次叉乘即可得到内角大于180度的点（下文称为凹点）。
由此我们可以从某一点遍历，找到第一个凹点，然后进入下一步
延长凹点起始边，进行相交测试
比如下图我们将会延长BC，并且相交于DE
那么如何得知BC延长线与DE相交呢：
我们举个例子，比如下图判断AB和CD相交，可以利用叉乘的特性，通过叉乘向量的朝向判断C与D是否在AB所成直线的同一方向。
ps:这里的叉乘法其实并不完善，下面会补充，读者可以想想什么情况失效。
回到刚才那张图片
得知凹点是C，则我们按照顺序从AB开始遍历检查BC是否与其相交，遍历到自己的时候显然需要跳过（BC跳过），且BC的下一条边DC由于C是凹点，也不可能和BC相交，所以也跳过。
求直线和直线的交点
可能会有人说不是求直线BC和线段相交吗，为啥是求直线和直线？因为BC是可以无限延伸的，并且我们已经判断了判断BC延长线与DE相交，排除了DE作为线段导致不够长的情况，所以只需将两者当成直线求交点即可。
一般有直线方程和叉乘两种办法求解，这里先介绍一下直线方程的办法
- 考虑k存在的一般情况
可以轻松求出两条直线的k和b
然后联立求出交点
即使某个直线求解出来的k为0，即直线为y = m也可以解出交点
- 考虑k不存在的情况
读者可能注意到，这里求k的时候可能有x2 = x1的情况，即直线为x = n，这时候前面的方法就失效了，所以需要特判某个直线不存在k，将x = n带入另一条直线
根据交点将凹多边形进行切割
得到交点F之后，我们需要将多边形数组分隔，此时根据边的顺序有和之前的边相交/之后的边相交两种情况，两种情况下分割出的多边形数组不一样
-
边延长之后和后续的边相交
-
边延长之后和前面的边相交
广度优先分割整个凹多边形
执行的步骤我们都已经得到了，那么有什么合适的办法可以让多边形的分割不断深入，直到每个多边形都成为凸多边形呢？答案是大家刷lc的时候会遇到的广度优先算法。我们需要一个队列存储待处理的所有多边形，在处理过程中每次弹出队首，遇到不可分割的多边形就加入答案队列，否则将拆分的多边形再次放入队尾。
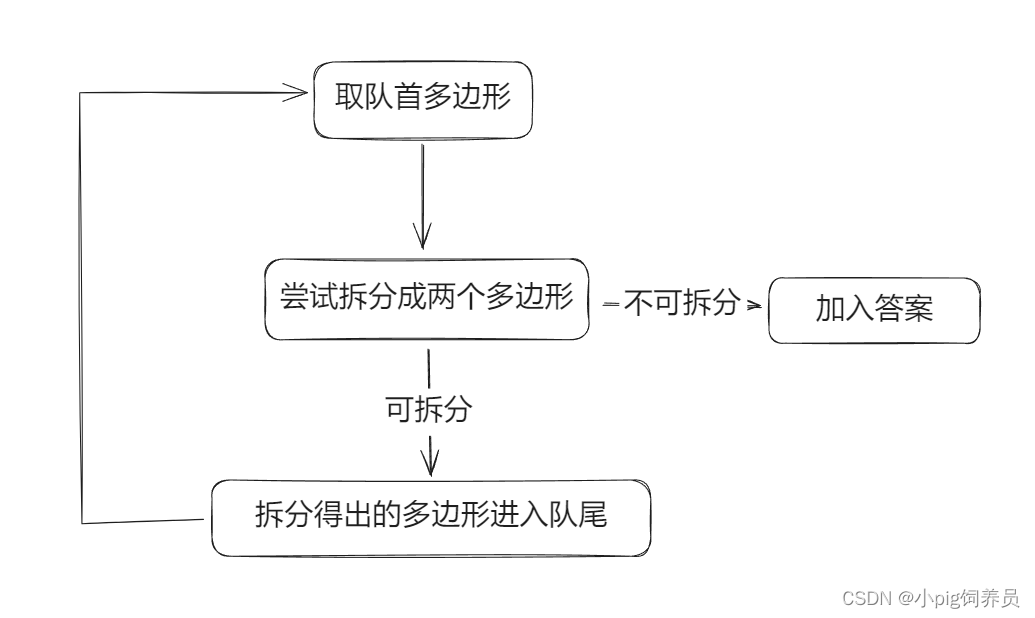
特殊情况：延长线和顶点相交
这里就是前面说的问题：
如下图，此时检测BC和DE相交/BC和EA相交，由于BC X BE = 0,所以会认为BC和DE/EA都不相交导致无法求得交点，这种情况可以归类为，延长线相交与多边形某一个顶点。
所以我们需要加入检测延长线交于某点的机制，当我们延长BC寻找相交边的时候，如果某个检测的边的终点满足延长边向量叉乘延长边指向边终点的向量叉乘为0向量，比如下图中BC X BE = 0向量，则说明延长边和DE边交于E。
这时候分割机制也要做对应调整：
-
相交的顶点为某个顺序在凹点之后的顶点
-
相交的顶点为某个顺序在凹点之前的顶点
-
效果验证
-
代码
入口为SperateConcavePolygon_Excute
public List<List<Vector3>> SperateConcavePolygon_Excute(List<Vector3> concavePolygon)
{
//最终得到的凸多边形答案组
List<List<Vector3>> ConvexPolygons = new List<List<Vector3>>();
//待处理的多边形队列
Queue<List<Vector3>> Polygons = new Queue<List<Vector3>>();
Polygons.Enqueue(concavePolygon);
while(Polygons.Count != 0)
{
List<Vector3> curPolygon = Polygons.Dequeue();
bool isConcave = SperateConcavePolygon(curPolygon, Polygons);//进行一次分割
if (!isConcave) ConvexPolygons.Add(curPolygon);//如果不可分割，进入答案组
}
return ConvexPolygons;
}
public bool SperateConcavePolygon(List<Vector3> concavePolygon, Queue<List<Vector3>> polygons)
{
bool isConcave = false;
for (int i = 0; i < concavePolygon.Count; i++)
{
Vector3 cur = concavePolygon[i]; //相交线起点
Vector3 next = concavePolygon[(i + 1) % concavePolygon.Count]; //，相交线终点
Vector3 nexts = concavePolygon[(i + 2) % concavePolygon.Count];//凹点下一个点
if (Vector3.Cross(next - cur, nexts - next).z < 0)//叉乘左手定则，逆时针下两边叉乘得到的结果指向外说明是凹点
{
Debug.DrawLine(cur, next, Color.yellow);
Debug.DrawLine(next, nexts, Color.yellow);
isConcave = true;
for (int j = 0; j < concavePolygon.Count; j++)
{
//跳过自己的边；以及下一条(凹点两条之间也不可能相交）
if (j == i || j == (i + 1 % concavePolygon.Count))
{
continue;
}
Vector3 interectStart = concavePolygon[j];//被延长线相交的边的起点
Vector3 interectEnd = concavePolygon[(j + 1) % concavePolygon.Count];//被延长线相交的边的终点
//叉乘法检测向量相交
if (Vector3.Cross(interectStart - cur, next - cur).z * Vector3.Cross(interectEnd - cur, next - cur).z < 0)
{
//Debug.DrawLine(interectStart, interectEnd, Color.blue);
//求出相交点
Vector3 intersection = getLineIntersection(cur, next, interectStart, interectEnd);
//延长线在相交线顺序之前,截取凹点到相交线起始点之间的点
List<Vector3> polygon1, polygon2;
if (i < j)
{
splitList(concavePolygon, (i + 1) % concavePolygon.Count, j, out polygon1, out polygon2);
polygon1.Add(intersection);
polygon2.Insert(i + 1, intersection);
}
else
{
splitList(concavePolygon, j + 1, i, out polygon1, out polygon2);
polygon1.Add(intersection);
polygon2.Insert(j + 1, intersection);
}
polygons.Enqueue(polygon1);
polygons.Enqueue(polygon2);
return isConcave;
}
//特殊情况，延长线相交与多边形某个点
else if(Vector3.Cross(interectStart-cur, next-cur) == Vector3.zero)
{
Vector3 intersection = interectStart; //交点为相交边起点
List<Vector3> polygon1, polygon2;
if (i < j)
{
splitList(concavePolygon, (i + 1) % concavePolygon.Count, j, out polygon1, out polygon2);
polygon2.Insert(i + 1, intersection);
}
else
{
splitList(concavePolygon, j , i, out polygon1, out polygon2);
polygon2.Insert(j, intersection);//公共点的前一个端点j-1的下一个即j
}
polygons.Enqueue(polygon1);
polygons.Enqueue(polygon2);
return isConcave;
}
}
}
}
return isConcave;
}
/// <summary>
/// 求两个线段的交点(非重合情况且一定存在交点的情况下)
/// </summary>
/// <returns></returns>
private Vector3 getLineIntersection(Vector3 start1, Vector3 end1, Vector3 start2, Vector3 end2)
{
float k1, b1, k2, b2;
if (start1.x == end1.x)
{
k2 = (end2.y - start2.y) / (end2.x - start2.x);
b2 = start2.y - k2 * start2.x;
return new Vector3(start1.x, k2 * start1.x + b2);
}
if(start2.x == end2.x)
{
k1 = (end1.y - start1.y) / (end1.x - start1.x);
b1 = start1.y - k1 * start1.x;
return new Vector3(start2.x, k1 * start2.x + b1);
}
//其他情况
k1 = (end1.y - start1.y) / (end1.x - start1.x);
b1 = start1.y - k1 * start1.x;
k2 = (end2.y - start2.y) / (end2.x - start2.x);
b2 = start2.y - k2 * start2.x;
float x = (b2 - b1) / (k1 - k2);
float y = k1 * x + b1;
return new Vector3(x, y, 0);
}
private void splitList(List<Vector3> list, int start, int end, out List<Vector3> list1, out List<Vector3> list2)
{
list1 = new List<Vector3>();
list2 = new List<Vector3>();
for (int i = 0; i < list.Count; i++)
{
if (i >= start && i <= end)
{
list1.Add(list[i]);
} else
{
list2.Add(list[i]);
}
}
}
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
