机器学习笔记 决策树

1.决策树的构造方法

1.1决策树定义

决策树就是一棵树，一颗决策树包含一个根节点、若干个内部结点和若干个叶结点；叶结点对应于决策结果，其他每个结点则对应于一个属性测试；每个结点包含的样本集合根据属性测试的结果被划分到子结点中；根结点包含样本全集，从根结点到每个叶子结点的路径对应了一个判定测试序列。

1.2决策树常用计算指标

信息熵定义：假如当前样本集D中第k类样本所占的比例为，K为类别的总数（对于二元分类来说，）。则样本集的信息熵为：

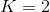
 其中信息熵越小说明数据纯度越高。

信息增益

  一般而言，信息增益越大，则表示使用特征  对数据集划分所获得的“纯度提升”越大。所以信息增益可以用于决策树划分属性的选择，其实就是选择信息增益最大的属性，ID3算法就是采用的信息增益来划分属性。

信息熵计算实例

计算过程

1.计算目标数据集D的信息熵

2.计算不同特征的信息熵

3.计算每个特征的信息增益

继续以上步骤得到完整的决策树：

 C4.5算法

信息增益率

CART

基尼系数

2.决策树剪枝

https://blog.csdn.net/u012328159/article/details/79285214

3.连续值处理

决策树（decision tree）(三)——连续值处理_天泽28的博客-CSDN博客_决策树连续值处理

当数据中的数据不是离散的时候，对连续序列a排序，两两计算平均值得到平均值集合{x}和排序后的序列a。去掉序列a中小于平均值的数，计算两个集合信息熵最后能得出在连续值属性取值为x时的信息增益。

4.缺失值处理

决策树（decision tree）（四）——缺失值处理_天泽28的博客-CSDN博客_决策树可以处理缺失值吗