向量点乘相关公式推导及 几何解释

1.向量点乘公式推导和几何解释

01.向量点乘(dot product)是其各个分量乘积的和，公式：

用连加号写：

向量a=(a1*e1, a2*e2,a3*e3........an*en)其中e1，e2，e3.......en为正交规范基（俩俩正交，每个向量单位为1）

向量b=(b1*e1, b2*e2,b3*e3........bn*en)其中e1，e2，e3.......en为正交规范基（俩俩正交，每个向量单位为1）

则向量a.b有下面的公式

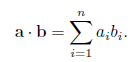
02.几何解释：

点乘的结果是一个标量，等于向量大小与夹角的cos值的乘积。

a•b = |a||b|cosθ

如果a和b都是单位向量，那么点乘的结果就是其夹角的cos值。

a•b = cosθ

03.推导过程：

假设a和b都是二维向量，θ1是a与x轴的夹角，θ2是b与x轴的夹角，向量a与b的夹角θ等于θ1 - θ2.

a•b = ax*bx + ay*by 

=  (|a|*sinθ1) * (|b| * sinθ2) +   (|a| * cosθ1) * (|b| * cosθ2)

= |a||b|(sinθ1*sinθ2 + cosθ1*cosθ2)

=|a||b|(cos(θ1-θ2))

= |a||b|cosθ

2.点乘交换率和分配率的推导

01.交换率

02.分配率

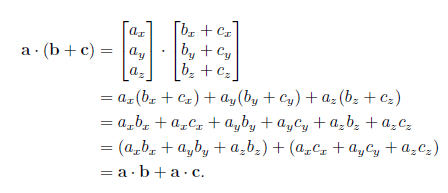
注：更多内容参见：<3D math primer for graphics and game development  second edition>点击打开链接

转载：https://blog.csdn.net/zsq306650083/article/details/8772128