【SVD】奇异值分解 -- 学习笔记

最新推荐文章于 2025-02-16 18:34:03 发布

萝卜丝皮尔

最新推荐文章于 2025-02-16 18:34:03 发布

阅读量1.8k

点赞数 2

分类专栏：数据挖掘与矩阵文章标签：机器学习矩阵

本文链接：https://blog.csdn.net/qq_43448491/article/details/104714656

版权

数据挖掘与矩阵专栏收录该内容

9 篇文章

订阅专栏

参考资料：数值分析

若A为Hermite阵，
可用-酉相似变换-将其化为对角形式： $Q^{*}AQ=\Lambda$ ，即得到谱分解，也就是特征值分解；
谱分解保持矩阵的秩和特征值不变。
若A非Hermite阵，

可用-初等变换-化为比较简单的对角形式，
$A=P\begin{bmatrix}I&0\\0&0\end{bmatrix}Q$
即满秩分解,保持矩阵的秩不变；
可用-相似变换-将其化为Jordan形，即Jordan分解， $A=PJP^{-1}$ ，保持矩阵的秩和特征值不变。
可用-酉相似变换-将其化为上三角形式，即Schur分解 $A = QRQ^{*}$ ，保持秩和特征值不变。
可用-酉变换-（不要求相似）j将其化为对角形式，即奇异值分解 $A=U\Sigma V^{*}$ ，特点是不要求A是方阵。

奇异值分解定理：
对任意矩阵 $A$ (可以不是方阵），存在酉矩阵U，酉矩阵V，对角元按非增次序排列的非负对角矩阵 $\Sigma$ ，使得： $A=U\Sigma V^{*}$ 。
其中，矩阵A的规模大小 = 对角矩阵 $\Sigma$ 规模大小。
上述是，完全奇异值分解（FULL SVD）。
还有经济型奇异值分解（economic svd），又称约化奇异值分解，此时 $A=U\Sigma V^{*}$ 中，非负对角矩阵是方阵（被约化了，其实是矩阵分块的运算的结果），代价是：在完全奇异值分解中较大的那个方阵不再是方阵（会更小，可能是扁的，也可能是高的）。

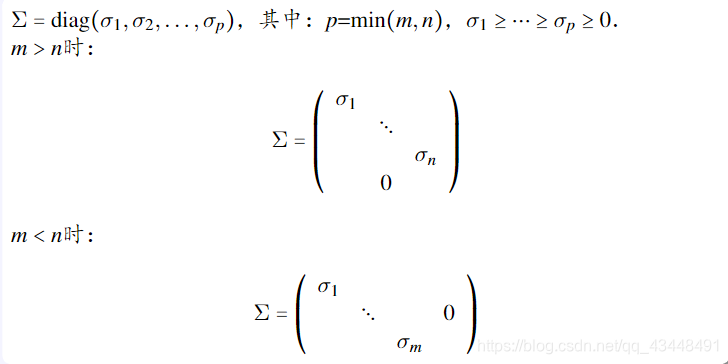
在这里插入图片描述

奇异值分解的性质：

矩阵A的秩 = 非零奇异值的个数 $r$ ；
原因：酉矩阵是可逆的，不改变矩阵的秩，即 $rank(A)=rank(\Sigma)$ .
矩阵A的值域 = 前 $r$ 个左奇异向量所张成的空间。

$A^{*}A$ 的非零特征值是矩阵A的非零奇异值的平方。

注： $|\Lambda|$ 表示对对角矩阵 $\Lambda$ 的每个元素取绝对值所组成的对角矩阵；
$sign(\Lambda)$ 表示对角矩阵 $\Lambda$ 的对角元的符号，在这里，如果非负，取1，否则取-1.

低秩逼近：
在这里插入图片描述
秩1矩阵，是指 $u_{j}v_{j}^{*}$ ，因为矩阵 $u_{j}$ 是列向量，所以它的秩为1，而矩阵的乘积的秩不大于每个因子矩阵的秩，所以秩为1.

在这里插入图片描述
说明：在所有-秩不超过k的-矩阵中，奇异值分解出的矩阵 $A_{k}$ 与矩阵A的二范数意义下最近，距离为第k+1个奇异值。

在F范数的意义下， $A_{k}$ 距离A也是最近的。

例题：
利用 $A^{*}A$ 的非零特征值是矩阵 $A$ 奇异值的平方，先求出奇异值，得到 $\Sigma$ 矩阵。
与此同时，求出 $A^{*}A$ 的特征向量，得到V矩阵。
利用 $U=AV\Sigma^{-1}$ ,求出矩阵U。
在这里插入图片描述

注：构造 $u_{3}$ 的方法有很多，比如： $u_{3}$ 与 $u_{2}$ 、 $u_{1}$ 向量正交， $u_{3}$ 的长度（二范数）为1，联立这三个方程即可求解。

阅读博客的笔记：
https://www.cnblogs.com/pinard/p/6251584.html
这篇博客从原理、应用等方面对SVD进行了详细介绍。
有些地方，值得做下笔记。
在这里插入图片描述
在PCA中，我们需要计算 $X^{T}X$ 矩阵的特征向量，可以考虑对矩阵 $X$ 进行SVD分解 $X=U\Sigma V^{T}$ ，那么 $X^{T}X=V\Sigma^{2}V^{T}$ ，也就是说右奇异矩阵正是我们所需要的： $X^{T}X$ 矩阵的特征向量。