树的结构知识构造及其实现 基础平衡霍夫曼

本篇文章结合这代码和图片进行多方面的讲解和呈现，细节的标识都以注释的形式展现，同样的，重点往往也是注释，有对比记忆点，也有一些理解的代换操作，目的是提高代码的健壮性和可读性。

二叉树一共有五种形态
null root left right 完全

二叉树

1. 二叉树是数据结构中一种重要的数据结构，也是树表家族最为基础的结构。
2. 二叉树的定义：二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。
3. 树的基础结点计算，通常用作于选择题
4. 在一棵二叉树中，若除最后一层外，其余层都是满的，则称此树是理想平衡树。理想平衡树包括满二叉树和完全二叉树。但并不一定是完全二叉树。
   普通的二叉树插入一个节点的复杂度是1，但是二叉排序树插入一个节点的时间复杂度是n，包括插入后的调整

/*

• 非空二叉树中度为0,1,2的结点个数分别为n0，n1，n2，则n0=n2+1，
• 叶子结点比二分支结点多一个，假设树中结点总数为n，则
• n=n0+n1+n2;
• n=n1+2n2+1，度为零的点就变成了叶子结点，比如满二叉树，就可以把单个结点理解为0，然后套用这个公式
• 高度为h的二叉树至多有2^h-1个结点
• 高度为h的m叉树至多有(m^h-1)/(m-1)个结点
• 使用等比数列求和
• 2^h-1-1<n<2h-1之间的范围，解出来
• 高为h的完全二叉树至少有2^{h-1，至多有（2}h）-1个结点，解出来涉及到取整

```cpp
若是将算法的叉数外延，变成高度为h的满m叉树
跟结点是第一层，第h层上的结点都是叶结点，其余各层上每一个结点都有m颗非空子树，正常从1开始标注
总结点是(2^h -1)/(m-1);
各层结点数m^(h-1)；
编号为i的结点的双亲结点存在，结点i的第一个子女的编号为j=（i-1）*m+1+1；反过来i的双亲结点编号就是【（i-2）/m】+1向下取整，跟结点没有双亲，所以i>1；
第k个子女结点的编号为（i-1）*m+k+1；

插入一个习题，通过有限的信息反推出总数目

/*
* 对于完全二叉树，可以由结点数n推出012的个数
* 完全二叉树最多只有一个度为1的结点
* n1=1/0
* n0=n2+1 ，则n0+n2肯定是奇数  //推理基础
* n0+n1+2*n2+n*nx=1+n1+n2+nx 可以求出n0的值
* 高度为m 的树中第i层有m^i-1个结点
* 高度为h的m叉树至多有m^k-1/(m-1)；
* 具有n个结点的m叉树最小高度为logm(n*(m-1)+1)
*/

二叉树的结构实现

根据一个基础模型进行数据的搭建

#define maxsize 100
#include "cmath"
//在计算二叉树的层数的时候，加上cmath头文件可以使用log函数
typedef int elemtype;
typedef struct treenode {
	elemtype data;
	struct treenode*lchild,*rchilde;
	struct treenode* parent;//父结点需要从root遍历，所以作为一个快速解决的途径
}binode,*bitree;//二叉树的顺序储存中，要求位置要一一对应,只利于完全二叉树
bitree root=NULL;//申明一个空结点的指针

上面是二叉树的结构，左右孩子跟结点，同时*bitree也就是多个结点的关联性，单个一个binode其实也可以理解为一棵树。我们所设定的bitree其实就是一个头结点，其实也是一棵树，我们可以把它理解成之后的森林里好多种树


具有n个结点的完全二叉树的高度为[log2（n+1）]或者[log2n]+1，n也在两者的公式中浮动
顺序存储结构链表中数组有存储。
且在n个结点的二叉链表中含有n+1个空链域。

二叉树的构造和基础功能实现

void init(bitree &t) {
	root = (bitree)malloc(sizeof(binode));
	root->data = 1;
	root->lchild = root->rchilde = NULL;//根结点
}
bool insert(bitree &t, elemtype n) {
	binode *p = (bitree)malloc(sizeof(binode));
	p->data = n;
	if (t->lchild == NULL) {
		p->data = n;
		p->rchilde = p->lchild = NULL;
		t->lchild = p;
		return true;
	}
	else if (t->rchilde == NULL) {
		p->data = n;
		p->rchilde = p->lchild = NULL;
		t->rchilde = p;
		return true;
	}
	else {
		return false;
	}
}
//按照某一种次序把所有终点都访问一遍
//先序遍历 递归压栈 二叉树的遍历更像是前中后缀的表达式

三种顺序排序
先序排列：就是根左右，
中序排列：就是左中右
后序排列 : 就是左右中
层序也就是层输出，
其实问题就是怎么递归作为一个队列式的插入弹出，可以考虑循环队列，（x+1）%100确定要插入的位置x就是rear或者font

void preorder(bitree t) {
	if (t != NULL) {
		//visit(t);输出还是检索，根据情况进行调试
		preorder(t->lchild);
		preorder(t->rchilde);
	}
}
//层序遍历，初始化一个辅助队列，根节点入队，若队列非空，则头结点出队，访问该结点的时候将其左右孩子压进栈，重复3直到队列为空
//判断二叉树是否为空
int IsEmptyBTree(bitree* bt)
{
	return bt == NULL ? 1 : 0;
}

//遍历二叉树，四种方法
//先序的方法输出
void PreOrder(bitree &bt)
{
	if (bt != NULL)
	{
		printf("%d ", bt->data);
		PreOrder(bt->lchild);
		PreOrder(bt->rchilde);
	}
}

//中序的方法输出
void MidOrder(bitree & bt)
{
	if (bt != NULL)
	{
		MidOrder(bt->lchild);
		printf("%c ", bt->data);
		MidOrder(bt->rchilde);
	}
}

//后序的方法输出
void PostOrder(bitree &bt)
{
	if (bt != NULL)
	{
		PostOrder(bt->lchild);
		PostOrder(bt->rchilde);
		printf("%c ", bt->data);
	}
}

//按层的顺序输出
void LevelOrder(bitree &bt)
{
	bitree* p = NULL;
	bitree* q[100] = { 0 };     
	int front = 0, rear = 0;
	if (bt)
	{
		rear = (rear + 1) % 100;
		q[rear] = bt;
	}
	while (front != rear)
	{
		front = (front + 1) %100;
		p = q[front];
		printf("%", p->data);
		if (p->left)
		{
			rear = (rear + 1) %100;
			q[rear] = p->left;
		}
		if (p->right)
		{
			rear = (rear + 1) % 100;
			q[rear] = p->right;
		}
	}
}

select综合

针对单一结点，通过耦合，也可以将一个很简单的函数进行嵌套和调用，这样你会发现，二叉树难的是它的递归逻辑。

//查找对应结点位置
ElemType* SearchBTree(bitree bt, ElemType e)
{
	if (bt == NULL)
		return NULL;
	else
	{
		if (bt->data == e)
			return &(bt->data);
		else
		{
			ElemType* p;
			if (p = SearchBTree(bt->lchild, e))
				return p;
			if (p = SearchBTree(bt->rchilde, e))
				return p;
			return NULL;
		}
	}
}

//求出一棵树的深度并返回
int DeepBTree(bitree bt)
{
	if (bt == NULL)
		return 0;
	else
	{
		int deep1 = DeepBTree(bt->lchild) + 1;
		int deep2 = DeepBTree(bt->rchilde) + 1;
		return deep1 > deep2 ? deep1 : deep2;
	}
}

//求一棵二叉树的结点总数
int BTreeCount(bitree bt)
{
	if (bt == NULL)
		return 0;
	else
		return BTreeCount(bt->lchild) + BTreeCount(bt->rchilde) + 1;
}

线索二叉树

结合之前用到过的算法，链表的形式把数上面的结点存储起来
平衡二叉树
霍夫曼** 这个多次考研都设计，
线索二叉树==前驱后继

/*
树的储存方式，顺序存储 双亲
孩子兄弟表示，链式表示
孩子表示法 链式+顺序

*/
/*
* 中序线索二叉树
* 前驱线索由左孩子充当，后继线索由右孩子充当
* 线索二叉树的结构
*/
typedef struct threadnode {
	elemtype data;
	struct threadnode* lchild, * rchild;
	int ltag, rtag;//1是线索，0是孩子
}threadnode,*threadtree;

线索的实战应用的实现
理解成链表可以方便考虑前驱和后继
线索二叉树是一种物理结构，是为了更好的find存储，
而二叉树是逻辑结构。
如果先序遍历序列和后序遍历序列正好相反，说明只有一个叶结点，而且每层只有一个结点，形如一个链表，高度等于其结点数。

• 中序线索树中，若某结点有右孩子，则其后继结点是它的右子树的最左下结点，RL;
  若某结点有左孩子，则其前驱结点就是它的左子树的最右下结点，LR；
  线索二叉树就是利用了刚才n+1的空指针域来存放前驱后继信息的
• 先序遍历有右孩子，那么左孩子就是后继，如果没有左孩子但是有右孩子，则右孩子就是后继，如果是叶结点，那么右链域直接指明了结点的后继.
• 先序遍历的后继比较简单，但是要查前驱需要知道双亲的位置。
• 后续结点的后继结点就比较复杂，如果x是二叉树的根，那么后链就是空，如果是双亲的右孩子或者双亲的左孩子但没有右子树，那么后继就是双亲；如果是亲的左孩子且双亲有右子树，那么后继就是双亲的右子树按后序遍历出的第一个结点。查找后序的前驱简单，后继需要知道双亲。
• 若有一个叶子结点是二叉树中的某一个子树的中序遍历结果序列的最后一个结点，则它一定是该子树的前序遍历结果序列的最后一个结点。而且后续遍历的复杂性在于双亲的存在才能研究后继问题。中序最省事，所以绝大多数都是用中序，前驱后继都能解决。

如何绘画线索树

• 首先正确逻辑构造二叉树，然后按照要求的顺序进行排序输出，当其没有左孩子的时候连接先序，没有右孩子连接后续，前序为空则是外接null，后续为空则是外延为null。

#include <stdio.h>
#include <mm_malloc.h>

// 测试用例：AB..CD... 或者 AB.DF..G..C.E.H..

typedef struct{
    char data;
    struct BiNode *LChild;
    struct BiNode *RChild;
    int Ltag;
    int Rtag;

}BiTNode,*BiTree;

BiTree pre  = NULL; //pre一定是要全局的，因为，他要始终跟在root后面的，指向前面一个被访问得节点，我最后得不到结果就是因为这里不是全局变量，而是使用void Inthread(BiTree root,BITree pre);这样是局部变量，不得的

int main(){
    void PreCreateBiTree(BiTree *T);
    void Inthread(BiTree root);
    BiTree InPre(BiTNode *p);
    BiTree InNext(BiTNode *p);
    void TInOrder(BiTree T);
    void InOrder(BiTree T);

    BiTree T ;
    //中序创建树
    PreCreateBiTree(&T);
    //然后将树线索化
    Inthread(T);
    //最后遍历树
    TInOrder(T);

}


//先序创建二叉树
void PreCreateBiTree(BiTree *T){//这里必须要用二级指针，不用你操作的结果根本拿不到，你可以先用一级指针思考一下，你就会发现真的很妙，

    char ch;
    ch = getchar();
    if (ch != '.'){
        *T = (BiTNode *)malloc(sizeof(BiTNode));
        (*T)->data = ch;
        (*T)->Ltag = 0;
        (*T)->Rtag = 0;
        PreCreateBiTree(&((*T)->LChild));//这个地方要传地址而不是temp->LChild，temp->LChild是等于NULL的，你要给这个变量的地址才行
        PreCreateBiTree(&((*T)->RChild));
    }else{
        *T = NULL;
    }
}

//线索化二叉树
void Inthread(BiTree root){

    if (root != NULL){
        Inthread(root->LChild);
        if (root->LChild == NULL){
            root->LChild = pre;
            root->Ltag = 1;
        }
        if (pre != NULL && pre->RChild == NULL){  //线索在过程中，这个结束条件时难想到的，pre为空且有孩子为空
                 pre->RChild = root;
                 pre->Rtag = 1;
        }
        pre = root;
        Inthread(root->RChild);
    }

}

//寻找中序遍历线索化的第一个节点
BiTree InFirst(BiTree T){

    BiTree p = T;
    if (p == NULL) return NULL;

    while(p->LChild !=NULL){  //由于你是中序遍历嘛，所以被访问的第一个节点肯定是最左边的左孩子
        p = p ->LChild;
    }
    return p;
}


// 在中序线索树中找节点前驱
/**
 *
 *        你结合中序遍历的特点你就会很清楚了
 *         如果当前节点p的Ltag=1的话那个他的前驱pre = p->Lchild
 *         不然的话，他肯定是当前节点的左子树中的最右边的一个节点，为什么呢？
 *         你想想我们要找的是p的前驱，那么在p的左边，按照左中右遍历的顺序，那么一定是p左边的部分节点的中最右边那个     
 * 最后被遍历出来的
 *        
*/
BiTree InPre(BiTNode *p){
    BiTree pre = NULL;
    if (p->Ltag == 1){
        pre = p->LChild;
    }else{
        pre =  p->LChild;
        while (pre->Rtag == 0){//p肯定是pre的后继，所以结束条件就是，pre->Rtag==1;
            pre = pre->RChild;
        }
    }
    return pre;

}

// 在中序线索树中找节点后继  思路是一样的
BiTree InNext(BiTNode *p){
    BiTree next = NULL;
    if (p->Rtag == 1){
        next = p->RChild;
    }else{
        next = p->RChild;
        while(next->Ltag == 0){
            next = next->LChild;
        }
    }
    return next;
}


//线索二叉树遍历，我只能说妙
void TInOrder(BiTree T){
    BiTree InFirst(BiTree T);
    BiTree InNext(BiTNode *p);
    //实在是太妙啦，你想想我们既然是中序遍历，那么我是不是要找到第一个节点出来，一旦找到后，那我们是不是可以利用找后及节点的函数，找到第二个元素
    //找到之后，我们是不是继续找到第二个节点的后继，是不是很妙
    BiTNode  *p;
    p = InFirst(T);
    while(p){
        printf("%c",p->data);
        p = InNext(p);//最后一个元素时没有后继的并且Lchild = NULL;因此，通过判断是否为NULL来作为结束条件
    }
}

递归思路

//一棵二叉树，左子树结点值小于根的结点值，小于右子树的结点值
//中序排序就是一个递增的数列 
typedef struct bstnode {
	int key;
	struct bstnode* lchild, * rchild;
}bstnode,*bstree;
//基础的定义结构在下面的二叉树的排序和操作
bstnode* bst_search(bstree t, int key) {
	while (t != NULL && key != t->key) {
		if (key < t->key)
			t = t->lchild;
		else
			t = t->rchild;
	}
	return t;
}//在二叉树上寻找值为key的点
//递归search 最坏的空间复杂度是0（h），节省了时间，如果使用上面的结构那么对应最坏空间复杂度是0（1）
bstnode* bstnodsearch(bstree t, int key) {
	if (t == NULL)
		return NULL;
	if (t->key == key)
		return t;
	else if (key < t->key)
		return  bstnodsearch(t->lchild, key);
	else 
		return  bstnodsearch(t->rchild, key);
}
int bst_insert(bstree& t, int k) {
	if (t == NULL) {
		t = (bstnode*)malloc(sizeof(bstnode));
		t->key = k;
		t->lchild = t->rchild = NULL;
		return 1;
	}
	else if (k ==t->key)
		return 0;
	else if (k < t->key)
		return bst_insert(t->lchild, k);
	else
		return bst_insert(t->rchild, k);
}

森林（多树~霍夫曼的前奏）

• 森林是m棵互不相交的数的集合，每棵树去掉跟结点后，其余各个子树又组成了森，访问森林里输的根节点之后，再递归，或者将其转化为二叉树，然后再递归。构造就是不断地插入根据不同的关键字序列，就会不同的结果
• 最后权值计算之和是永远一致的与ASL求寻找的平均时间复杂度区分开，等概率查找的时候，查找成功就是每一项的查找次数合/n，查找失败是各叶结点延伸后点的查找项合/n+外加一个结点的1.
• 最佳二叉排序树应该是高度最小的二叉排序树。
• 树转化二叉树的方法是A兄弟直接加一条线，B每个结点保留第一个孩子的线，其他抹去C树根为轴心，右顺时针45度。
• 森林变成二叉树的方法是A将森林中的每棵树转换成相应的二叉树，也就是copy上面的方法，然后每棵树的根也可以作为兄弟关系，在每棵树的根之间加上一根连线，第一棵树的轴心顺时针45度。
• 树或者森林变成二叉树就是将单一支的树变成左子树，然后将下一组单支子树变成A的右子树或者是右孩子，依次向右递接。

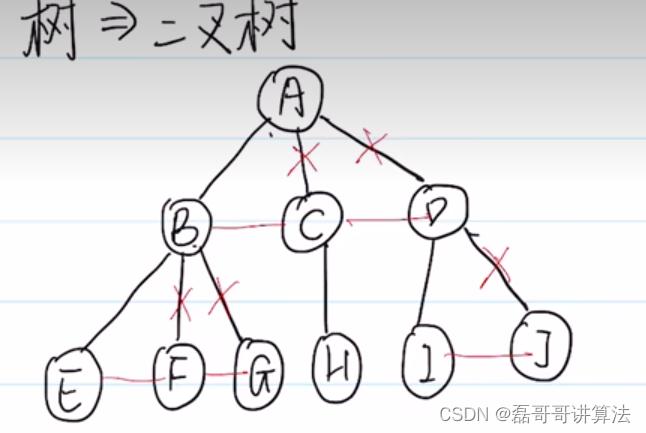
树 二叉树 森林 辗转腾挪

• 树变成二叉树

1. 第一步兄弟加线
2. 除长子外的去掉
3. 层次调整
   
   

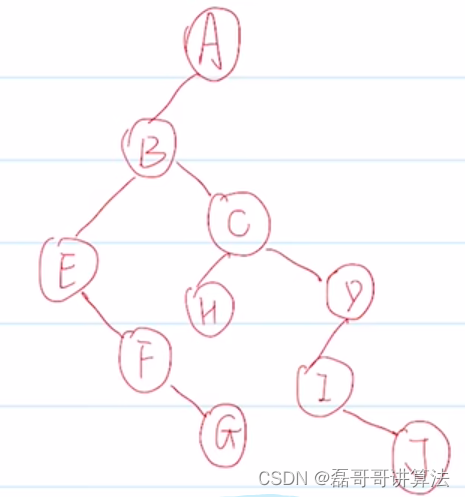
• 二叉树变成树或者森林

4. 如果该结点的左孩子存在，那么就将该结点的左孩子的右节点，右节点的右节点依次与其连线
5. 然后依次去除与右孩子的连线
6. 对其进行层次调整
   

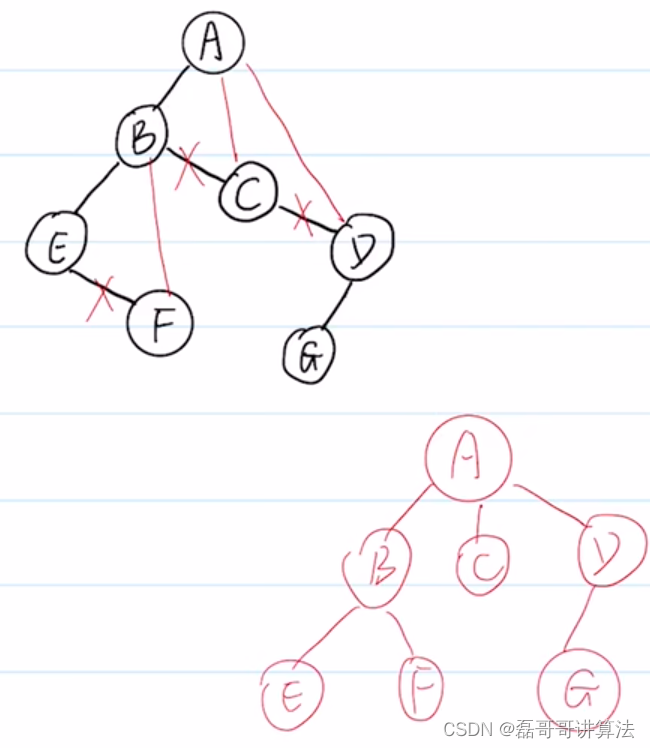
• 二叉树变成森林

7. 能否变成的前提是，二叉树的跟结点是否是右孩子，有就是森林
8. 寻找右孩子去线，将分离的二叉树转换成树
9. 观察树是否健康，例如下面的A和C结点树可以使用上面二叉树变成树的方法进优化调整
   

AVL平衡二叉树L or R

• 平衡二叉树 AVL数，树上任一个结点的左右子树的高度差不差过一
• 结点的平衡因子=左子树高-右子树高左子树群减去右子树群的值浮动于0，1，-1之间。
• 特殊的二叉排序树，提高了查找效率，左子树减去右子树高度之差是1的绝对值
• 定值比较的关键个数不超过树的深度，假设以nh表示树的深度为h的平衡树中含有的最少结点数。
• n0=0，n1=1，n2=2; 并且 nh=nh-1+nh-2+1的递推公式。含有n个平衡二叉树的最大深度为log2n，因此平均查找长度为log2n。
• 以平衡因子失衡的点位根，进行R和L的判断，随后使用递归下移计算就行，
• 换成语言描述，因为加入了R的R后使得root失衡所以进行RR操作

哈夫曼树

• 哈夫曼树编码
• 权值，结点有权，
  *结点的带权路径长度，从树的根到该结点的路径长度（经过的边数）与该结点上权值的乘积
  *数的带权路径长度，所有端叶节点的带权路径之和
• 在含有n和带权叶子结点的二叉树中，其中带权路径长度最小的二叉树，叫做哈夫曼树，也叫最优二叉树WPL是最小值
• 构造过程中一共新建了n-1各结点作为双分支结点，所以全部的结点是2n-1
• 且huffman树只有点位0和2，所以n0=n2+1，n2=n-1；

typedef struct Node
{
	int weight;                //权值
	int parent;                //父节点的序号，为-1的是根节点
	int lchild, rchild;         //左右孩子节点的序号，为-1的是叶子节点
}HTNode, * HuffmanTree;          //用来存储哈夫曼树中的所有节点
typedef char** HuffmanCode;    //用来存储每个叶子节点的哈夫曼编码

/*
* 哈夫曼编码的实现
*/
#include<iostream>
#include<cstdlib>
#include<algorithm>
#include<cstdio>
using namespace std;
struct BTreeNode
{
	int data;
	struct BTreeNode* left;
	struct BTreeNode* right;
};
//一般打印输的结点
void Print_BTree(struct BTreeNode* BT)
{
	if (BT != NULL)
	{
		printf("%d", BT->data); //输出根结点的值
		if (BT->left != NULL || BT->right != NULL)
		{
			printf("(");
			Print_BTree(BT->left); //输出左子树
			if (BT->right != NULL)
				printf(",");
			Print_BTree(BT->right); //输出右子树
			printf(")");
		}
	}
}
//创建一颗哈夫曼树
struct BTreeNode* CreateHuffman(int a[], int n)
{
	struct BTreeNode** b;//结构体指针的指针b作为指针数组
	struct BTreeNode* q;//定义一个结构体P
	b = (BTreeNode**)malloc(n * sizeof(struct BTreeNode*));
	//对指针数组b进行初始化
	for (int i = 0; i < n; i++)//初始化b指针数组，使每个指针元素指向a数组中对应的元素结点
	{
		b[i] = (BTreeNode*)malloc(n * sizeof(struct BTreeNode*));
		b[i]->data = a[i];
		b[i]->left = NULL;
		b[i]->right = NULL;
	}
	//利用循环创建一颗哈夫曼树
	for (int i = 1; i < n; i++)//一共进行n-1次循环
	{
		int k1 = -1, k2;
		for (int j = 0; j < n; j++)//让k1初始指向森林中第一棵树，k2指向第二棵
		{
			if (b[j] != NULL && k1 == -1)
			{
				k1 = j;
				continue;
			}
			if (b[j] != NULL)
			{
				k2 = j;
				break;
			}
		}
		//从当前除过第一个结点之外的最小的那个结点
		for (int j = k2; j < n; j++)
		{
			if (b[j] != NULL)
			{
				if (b[j]->data < b[k1]->data)
				{
					k2 = k1;
					k1 = j;
				}
				if (b[j]->data > b[k2]->data)
				{
					k2 = j;
				}
			}
		}
		//利用最小值数和次小值树，建立哈夫曼树，将每次返回树根指针q;
		q = (BTreeNode*)malloc(sizeof(struct BTreeNode));
		q->data = b[k1]->data + b[k2]->data;//树根结点存放的是总路径
		q->left = b[k1];
		q->right = b[k2];
		b[k1] = q;//更新结点（将最新的根节点付给b[k1]当作是新的根节点）
		b[k2] = NULL;//将b[k2]指针置空
	}
	free(b);//将建立的动态数组释放
	return q;//放回根节点的指针
}
//求哈夫曼树的路径长度
int WeightPathLength(struct BTreeNode* FBT, int len)//len初始为0
{
	if (FBT == NULL) //空树返回0
		return 0;
	else
	{
		if (FBT->left == NULL && FBT->right == NULL)//访问到叶子结点
			return FBT->data * len;
		else //访问到非叶子结点，进行递归调用，返回左右子树的带权路径长度之和，len递增
			return WeightPathLength(FBT->left, len + 1) + WeightPathLength(FBT->right, len + 1);
	}
}
//哈夫曼树解码
void Coding(struct BTreeNode* FBT, int len)
{
	static int a[10];//用来存储密码0  1
	if (FBT != NULL)
	{
		if (FBT->left == NULL && FBT->right == NULL)
		{
			printf("j结点权值为 %d 的编码:", FBT->data);
			for (int i = 0; i < len; i++)
			{
				cout << a[i] << " ";
			}
			cout << endl;
		}
		else
		{//遍历的层数加1
			a[len] = 0;//左节点为0
			Coding(FBT->left, len + 1);//采用递归实现
			a[len] = 1;//右结点为1
			Coding(FBT->right, len + 1);
		}
	}
}

核心代码融合详解，线索 AVL Huffman

// two binary tree.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//

#include <iostream>
using namespace std;
typedef struct binode {
    int data;
    struct binode* lchild, * rchild;
}binode,*bitree;
void init() {
    binode* p = (binode*)malloc(sizeof(binode));
    p->data = -1;
    p->lchild = p->rchild = NULL;
}
bool insertnode(bitree T, int n) {
    binode* p = (binode*)malloc(sizeof(binode));
    p->data = n;
    if (T->lchild == NULL) {
        p->rchild = p->lchild = NULL;
        T->lchild = p;
        return true;
    }
    else if (T->rchild == NULL) {
        p->rchild = p->lchild = NULL;
        T->rchild = p;
        return true;
    }
    else return false;
}
typedef struct TheardNode {
    int data;
    TheardNode* lchild, * rchild;
    int ltag, rtag;//tag是作为有孩子的时候0，没有孩子的时候为了不浪费所以变成了指针去指向前驱后继
}ThreadNode,*threadlist;
//构造中序线索二叉树
void inthread(threadlist& p, threadlist& pre) {
    if (p != NULL) {
        inthread(p->lchild, pre);
        if (p->lchild == NULL) {
            p->lchild = pre;
            p->ltag = 1;
        }
        if (pre != NULL && pre->rchild == NULL) {
            pre->rchild = p;
            pre->rtag = 1;
        }
        pre = p;
        inthread(p->rchild,pre);
    }
}//线索化
ThreadNode* inordernext(ThreadNode *P) {
    threadlist q = NULL;
    if (P->rtag == 1)return P->rchild;
    else {
        q = P->rchild;
        while (q->ltag == 0)q = q->lchild;
    }
    return q;
    // 走到最左边然后线索化找后继，后继完了找右子树中第一个访问结点
}
void orderprint(ThreadNode* T) {
    if (T != NULL) {
        while (T->ltag == 0)T = T->lchild;
        do {
            printf("%d ", T->data);
            T = inordernext(T);
        } while (T != NULL);
    }
}
#define maxsize 50
int btdepth(threadlist L) {
    if (!L)return 0;
    int front = -1, rear = -1;
    int last = 0, level = 0;
    ThreadNode* q[maxsize];
    q[++rear] = L;
    ThreadNode* p;
    while (front < rear) {
        p = q[++front];
        if (p->lchild)q[++rear] = p->lchild;
        if (p->rchild)q[++rear] = p->rchild;
        if (front == rear)level++;
        last = rear;
    }
    return level;
}//使用了非递归的方式
int bidepth(threadlist L) {
    if (L == NULL) {
        return 0;
    }
    int ldepth = btdepth(L->lchild);
    int rdepth = btdepth(L->rchild);
    if (ldepth > rdepth)return ldepth + 1;
    else return rdepth + 1;
}
const int N = 1e5 + 10;
int pos[N]; int n;

ThreadNode* memory(int a[], int b[], int l1, int r1, int l2, int r2) {
   ThreadNode* root = (ThreadNode*)malloc(sizeof(ThreadNode));
   root->data = a[l1];
   int i;
   for (i= l2; b[i] != root->data; i++);//通过中序和前序确定root的排列位置 
   int llen = i - l2;
   int rlen = r2 - i;
   if (llen)root->lchild = memory(a, b, l1, l1 + llen, l2, l2 + llen - 1);
   else root->lchild = NULL;
   if (rlen)root->rchild = memory(a, b, r1 - rlen + 1, r1, r2 - rlen + 1, r2);
   else root->rchild = NULL;
   return root;
}
//计算度为2的个数
int doublenode(threadlist L) {
    if (L == NULL)return 0;
    else if (L->lchild != NULL && L->rchild != NULL)return doublenode(L->lchild) + doublenode(L->rchild) + 1;
    else return doublenode(L->lchild) + doublenode(L->rchild);   
}
int i;//全局变作为跟着变化
int Prenode(threadlist L,int k) {
    if (L == NULL) return '#';
    if (i == k)return L->data;
    i++;
    int ch = Prenode(L->lchild, k);
    if (ch != '#')return ch;
    ch = Prenode(L->rchild, k);
    return ch;
    }
//删除某点作为根的结点
void deletenode(threadlist L) {
    if (L) {
        deletenode(L->lchild); deletenode(L->rchild);
        free(L);
    }
}
#include<queue>
void search(threadlist L, int x) {
    threadlist q[maxsize];
    if (L) {
        if (L->data == x)deletenode(L);
        queue<ThreadNode*>q;
        while (!empty(q)) {
            q.push(L);
            if (L->lchild) {
                if (L->lchild->data == x) {
                    deletenode(L->lchild); L->lchild = NULL;
                }
                else q.push( L->lchild);
            }
            if (L->rchild) {
                if (L->rchild->data == x) {
                    deletenode(L->rchild); L->rchild = NULL;
                }
                else q.push(L->rchild);
            }
        }
    }

}
//找p和q的公共祖先后续遍历较好
//带权二叉树
typedef struct Binode {
    int weight;
    Binode* lchild, * rchild;
}Binode,*Bitree;
int wpl(Bitree root) {
    return wpi_preorder(root, 0);
}
int wpi_preorder(Bitree root, int deep) {
    static int wpl = 0;
    if (root->lchild == NULL && root->rchild == NULL)wpl += deep * root->weight;
    if (root->rchild != NULL)wpi_preorder(root->lchild, deep++);
    if (root->rchild != NULL)wpi_preorder(root->rchild, deep++);
}//前序
int wpl_levelorder(Bitree root) {
    Bitree q[maxsize];
    int end1 =0, end2 = 0;
    int wpl = 0, deep = 0;
    Bitree lastnode, newlastnode=NULL;
    lastnode = root;
    q[end2++] = root;//现存的各类数据
    while (end1 != end2) {
        Bitree t = q[end1++];
        if (t->lchild == NULL && t->rchild == NULL)wpl += deep *t->weight;
        if (t->lchild != NULL)q[end2++] = t->lchild; newlastnode = t->lchild;
        if (t->rchild != NULL)q[end2++] = t->rchild; newlastnode = t->rchild;
        if (t == lastnode)lastnode = newlastnode; deep += 1;
    }
    return wpl;
}
//双亲表示法
typedef struct {
    int data;
    int parent;
}Ptnode;
typedef struct {
    Ptnode nodes[maxsize];
    int n;
}Ptree;
//孩子法，直接做链表类似于图的样式
typedef struct cbpnode {
    int data;
    cbpnode* child, *bro, *parent;
}cbpnode,*cbplist;
//并查集
int UFset[maxsize];
void initial(int s[],int n) {
    for (int i = 0; i <n; i++) {
        s[i] = i;
    }
}
int find(int s[], int x) {
    while (s[x] >= 0)x = s[x];
    return x;
}
void setunion(int s[], int root1, int root2) {
    s[root2] = root1;
}
int bst_insert(Bitree& T, int key) {
    if (T == NULL) {
        T = (Binode*)malloc(sizeof(Binode));
        T->weight = key;
        T->lchild = T->rchild = NULL;
        return 1;
    }
    else if (key == T->weight)return 0;
    else if (key < T->weight)return bst_insert(T->lchild,key);
    else return bst_insert(T->rchild, key);
}
//删除的时候需要考虑三种情况在第三种情况时，删除后以中序排序的第一个子女补上
//平衡二叉树左子树-右子树的总数
typedef struct avlnode {
    int data;
    int balance;//由height计算出来的
    int height;
    avlnode* lchild, * rchild;
}avlnode,*avltree;//log2n
//调整子树的时候选择最小不平衡子树，可以判断左右旋，然后将根旋转，最后将尾数挂上去，可以根据大小排列一下决定排序树的大小
// LR左孩子的右孩子加上，先左旋后右旋调整，RL相反，操作无差别
avltree creatnode(int x) {
    avltree newnode = (avltree)malloc(sizeof(avlnode));
    newnode->data = x;
    newnode->height = 0;
    newnode->lchild = newnode->rchild = NULL;
    return newnode;
}
//判断是否是平衡二叉树
bool Judge_avl(avlnode* bt, int& balance, int& h) {
    int bl = 0, br = 0, hl = 0, hr = 0;
    if (bt == NULL) { h = 0; balance = 1; }
    else if (bt->lchild == NULL && bt->rchild == NULL) {
        h = 1; balance = 1;
    }
    else {
        Judge_avl(bt->lchild, bl, hl);
        Judge_avl(bt->rchild, br, hr);//递归传值
        h = max(hl, hr) + 1;
        if (abs(hl - hr) == 2)balance = bl && br;
        else balance = 0;
    }
}

int getheight(avltree root) {
    if (!root)return -1;
    else return root->height;
}
int getmax(int a, int b) {
    if (a > b)return a;
    else return b;
}
//思路是因为点的变动使得某点的平衡因子出现》=2的情况，所以以这个变换的平衡因子点出发，包含自身的三个点，也就是对于旋转参数的考核，是LL,LR,RR,RL等，然后LL RR以此平衡点作为root，下一个点位temp，如果是RL,LR那么就进行两次旋转，root的下一个作为首轮旋转root，然后首轮root的下一个点是temp，以此类推。返回到二轮，也就是因子的点作为二轮旋转点
//在左右旋的时候会将height计算进去，因为随着添加，层数的不确定性，一个一个计算麻烦
avltree Rtrot(avlnode* root) {//右单旋，也就是LL
    avlnode* temp;
    temp = root->lchild;
    root->lchild = temp->rchild;
    temp->rchild = root;
    root->height = getmax(getheight(root->lchild), getheight(root->rchild)) + 1;
    temp->height = getmax(getheight(temp->lchild), root->height) + 1;
    return temp;
}
avltree Ltrot(avlnode* root) {//左单旋 RR
    avlnode* temp = (avltree)malloc(sizeof(avlnode));
    temp = root->rchild;
    root->rchild = temp->lchild;
    temp->lchild = root;
    root->height = getmax(getheight(root->lchild), getheight(root->rchild)) + 1;
    temp->height = getmax(getheight(temp->rchild), root->height) + 1;
    return temp;
}
avltree LRtrot(avlnode* root) {
    //先左后右
    root->lchild = Ltrot(root->lchild);
    return Rtrot(root);
}
avltree RLrot(avlnode* root) {
    root->rchild = Rtrot(root->rchild);
    return Ltrot(root);
}
//LL LR RR RL &&height
avltree createavltree(avltree root, int x) {
    if (!root) {
        root = creatnode(x); return root;
    }
    else if (x < root->data) {
        root->lchild = createavltree(root->lchild, x);
        if (getheight(root->lchild) - getheight(root->rchild) == 2) {
            if (x < root->lchild->data)root = Rtrot(root);
            else root = LRtrot(root);
        }
    }
    else if (x > root->data) {
        root->rchild = createavltree(root->rchild, x);
        if (getheight(root->rchild) - getheight(root->lchild) == 2) {
            if (x > root->rchild->data)root = Ltrot(root);
            else return root = LRtrot(root);
        }
    }
    root->height = getmax(getheight(root->lchild), getheight(root->rchild)) + 1;
    return root;
}
avltree find(avltree root, int x) {
    if (!root)return NULL;
    if (x < root->data)return find(root->lchild, x);
    else if (x > root->data)return find(root->rchild, x);
    else return root;
}
avltree findleftmax(avltree root) {
    if (root->lchild)return findleftmax(root->lchild);
    return root;
}

删除平衡二叉树

第一步删除 第二步审核因子或者深度是否出现变化
平衡二叉树是最优的二叉排序树，因此也有雷同的点，只是在排序结束之后要重新审核左右孩子的深度，平衡因子进行考虑
一共有三种情况
第一种情况是 被删除的节点为叶子节点，就是找到了删除的节点
第二种就是删除的节点有左子树或者右子树
第三种情况就是两边孩子都有，自己作为root的删除
通过 root h h-1图像来进行的模拟，可以将左子树上节点删除等价为右子树重新插入了一个新节点，同理也相反运行

回溯判断因子的是否出现变换，如果有问题就进行旋转操作
① 将该结点直接从树中删除；
② 其父节点的子树高度的变化将导致父结点平衡因子的变化，通过向上检索并推算其父结点是否失衡；
③ 如果其父结点未失衡，则继续向上检索推算其父结点的父结点是否失衡…如此反复②的判断，直到根结点；如果向上推算过程中发现了失衡的现象，则进行④的处理；
④ 如果其父结点失衡，则判断是哪种失衡类型[LL、LR、RR、RL]，并对其进行相应的平衡化处理。如果平衡化处理结束后，发现与原来以父节点为根结点的树的高度发生变化，则继续进行②的检索推算；如果与原来以父结点为根结点的高度一致时，则可说明父结点的父结点及祖先结点的平衡因子将不会有变化，因此可以退出处理。

删除节点有左子树或右子树的处理步骤如下：
① 将左子树（右子树）替代原有删除结点的位置；
② 结点C被删除后，则以C的父结点B为起始推算点，依此向上检索推算各结点（父、祖先）是否失衡；
③ 如果其父结点未失衡，则继续向上检索推算其父结点的父结点是否失衡…如此反复②的判断，直到根结点；如果向上推算过程中发现了失衡的现象，则进行④的处理；
④ 如果其父结点失衡，则判断是哪种失衡类型[LL、LR、RR、RL]，并对其进行相应的平衡化处理。如果平衡化处理结束后，发现与原来以父节点为根结点的树的高度发生变化，则继续进行②的检索推算；如果与原来以父结点为根结点的高度一致时，则可说明父结点的父结点及祖先结点的平衡因子将不会有变化，因此可以退出处理

可以有两种解决办法：第一种左子树max值但是第二方法删左子树min有弊端
1.找到左子树中的最大值，将值赋给给节点，然后将左子树最大值这个节点删除(删除可以用递归实现)也就是找到删除点中序遍历的前驱
变成了单源子树情况。

Btree *BalanceTreeDelet(Btree **tree, ElementType x){
	if (*tree == NULL){return null;}
	if ((*tree)->data < x){
		//递归返回为右子树，说明删完了
		(*tree)->right = BalanceTreeDelet(&(*tree)->right, x);
		//判断，该结点平衡因子是否被破坏
		if (GetHight((*tree)->left) - GetHight((*tree)->right) == 2){
			//如果被破坏，左孩子结点
			if (GetHight((*tree)->left->left) - GetHight((*tree)->left->right) == 1){
				Ltrot(tree);
			}
			else{
				LRtrot(tree);
			}
		}
	}
	else if ((*tree)->data > x){
		//递归返回为左子树
		(*tree)->left = BalanceTreeDelet(&(*tree)->left, x);
		//判断，该结点是否被破坏
		if (GetHight((*tree)->left) - GetHight((*tree)->right) == -2){
			//右孩子结点
			if (GetHight((*tree)->right->left) - GetHight((*tree)->right->right) == -1){
				Rtrot(tree);
			}
			else{
				RLtrot(tree);
			}
		}
 
	}//这个就是删除之后的回溯，也是找到删除核心点的位置。
	//找到
	else{//删除点的中序遍历前驱
		if ((*tree)->left && (*tree)->right){
			Btree *temp = Getmax((*tree)->left);
			int x = temp->data;
			(*tree)->data = x;
			(*tree)->left = BalanceTreeDelet(&(*tree)->left, x);
			//这里也需要调整
			if (GetHight((*tree)->left) - GetHight((*tree)->right) == -2){
				//左孩子结点
				if (GetHight((*tree)->right->left) - GetHight((*tree)->right->right) == -1){
					Rtrot(tree);
				}
				else{
					RLtrot(tree);
				}
			}
 
		}
		else if ((*tree)->left == NULL && (*tree)->right){
			Btree *temp = *tree;
			*tree = (*tree)->right;
			free(temp);
 
		}//只有右子树
		else if ((*tree)->left && (*tree)->right  == NULL){
			Btree *temp = *tree;
			*tree = (*tree)->left;
			free(temp);
 
		}//第二种情况的只有左子树
		else{
			Btree *temp = *tree;
			*tree = NULL;
			free(temp);
		}//都没有只是删除叶子
	}
	return *tree;
}

下面的代码是容易理解的复杂描述，使用递归最好用上面的嵌套就可以了

bool deleteAVL(LPNode* root, int key)
{
	if (*root == NULL)
		return false;
	if (key == (*root)->key)
	{
		LPNode q, s;
		if ((*root)->left == NULL && (*root)->right == NULL)
		{
			q = (*root);
			(*root) = NULL;
			delete q;
		}
		else if ((*root)->left == NULL)
		{
			q = (*root);
			*root = (*root)->right;
			delete q;
		}
		else if ((*root)->right == NULL)
		{
			q = *root;
			*root = (*root)->left;
			delete q;
		}
		else
		{
			q = *root;
			s = (*root)->left;
			while (s->right)
			{
				q = s;
				s = s->right;
			}
			(*root)->key = s->key;
			if (q != *root)
			{
				q->right = s->left;
			}
			else
			{
				q->left = s->left;
			}
		}
		return true;
	}
	else if (key > (*root)->key)
	{
		//如果本次传进去删掉了(*root)->right，那么return回来就是true，则需要调整(*root)
		//否则没有删掉，返回回来是false，则不需要调整
		int flag = deleteAVL(&(*root)->right, key);
		if (flag)
		{
			//更新节点深度
			renewTreeDepth(*root);
			//二叉树平衡的调整
			adjustBalance(root, key);
		}
		return flag;
	}
	else
	{
		//如果本次传进去删掉了(*root)->left，那么return回来就是true，则需要调整(*root)
		//否则没有删掉，返回回来是false，则不需要调整
		int flag = deleteAVL(&(*root)->left, key);
		if (flag)
		{
			//更新节点深度
			renewTreeDepth(*root);
			//二叉树平衡的调整
			adjustBalance(root, key);
		}
		return flag;
	}
}

删除二叉搜索树

/第一种情况：没找到删除的节点，遍历到空节点直接返回了
找到删除的节点
第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点
第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）
放到删除节点的右子树的最左面节点的左孩子上，
返回删除节点右孩子为新的根节点。/

avltree deletbstnode(avltree root, int x) {
    avlnode* temp;
    // 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点
    if (!root)return NULL;
    else if (x < root->data)root->lchild = deleteavl(root->lchild, x);
    else if (x > root->data)root->rchild = deleteavl(root->rchild, x);
    //第一种情况能找到删除的点
    else {
    // 第五种情况：左右孩子节点都不为空，则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置 并返回删除节点右孩子为新的根节点。
        if (root->lchild && root->rchild) {
            temp = findleftmax(root->lchild);
            root->data = temp->data;
            root->lchild = deleteavl(root->lchild, root->data);
        }
        else {
            temp = root;
           // 第三种情况：其左孩子为空，右孩子不为空，删除节点，右孩子补位 ，返回右孩子为根节点
            if (root->lchild)root = root->lchild;
           // 第四种情况：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
            else if (root->rchild)root = root->rchild;
            else root = NULL;
            free(temp);
            temp = NULL;
        }
        return root;
    }
}
//霍夫曼树的构造用class实现
typedef struct huffmance {
    int weight;
    int lchild,  rchild,parent;
    
}huffnode,*hufftree;
//构建堆操作
 void select(hufftree &Ht,int n,int &s1,int &s2) {
     int minum;
     for (int i = 1; i <= n; i++) {
         if (Ht[i].parent == 0)minum = i;break;
     }
     for (int i = 1; i <= n; i++){
         if (Ht[i].parent == 0)
             if (Ht[i].weight < Ht[minum].weight)minum = i;
     }
     s1 = minum;
     for (int i = 1; i <= n; i++) {
         if (Ht[i].parent == 0 && i != s1) minum = i; break;
     }
     for (int i = 1; i <= n; i++) {
         if (Ht[i].parent == 0 && i != s1) {
             if (Ht[i].weight < Ht[minum].weight)minum = i;
         }
     }
     s2 = minum;
}
 void creathuffman(hufftree &HT, int* w, int n) {
     int m, s1, s2;
     m = n * 2 - 1;  // 总结点的个数
     HT = new huffnode[m + 1]; // 分配空间
     for (int i = 1; i <= n; i++) // 1 - n 存放叶子结点，初始化
     {
         HT[i].weight = w[i];
         HT[i].parent = 0;
         HT[i].lchild = 0;
         HT[i].rchild = 0;
     }
     for (int i = n + 1; i <= m; i++)   // 非叶子结点的初始化
     {
         HT[i].weight = 0;
         HT[i].parent = 0;
         HT[i].lchild = 0;
         HT[i].rchild = 0;
     }
     for (int i = n + 1; i <= m; i++)     // 创建非叶子节点，建哈夫曼树
     {   // 在HT[1]~HT[i-1]的范围内选择两个parent为0且weight最小的两个结点，其序号分别赋值给 s1 s2
         select(HT, i - 1, s1, s2);
         HT[s1].parent = i;  // 删除这两个结点
         HT[s2].parent = i;
         HT[i].lchild = s1;      // 生成新的树，左右子节点是 s1和s2
         HT[i].rchild = s2;
         HT[i].weight = HT[s1].weight + HT[s2].weight;   // 新树的权�?
         printf("%d (%d, %d)\n", HT[i].weight, HT[s1].weight, HT[s2].weight);
     }//类似补充到新的结点放置在数组表里
 }
int main()
{
    std::cout << "smelly cat!\n";
}

B树

B树的定义：

• B树(B-tree)是一种树状数据结构，它能够存储数据、对其进行排序并允许以O(log n)的时间复杂度运行进行查找、顺序读取、插入和删除的数据结构。B树，概括来说是一个节点可以拥有多于2个子节点的二叉查找树。

B树的特征：

• 根节点至少有两个子节点
  每个中间节点都包含k-1个元素和k个孩子，其中 m/2 ≤ k ≤ m (m为树的阶)
  每个叶子节点都包含k-1个元素，其中 m/2 ≤ k ≤ m (m为树的阶)
  每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域划分(一个结点有k个孩子时，必有k-1个元素才能将子树中所有元素划分为k个子集)

that is all 文章内容优化后第三改 leo