废话文学
图论和树的习题代码题有点小难,所以研究了一下,将网上的执行题敲外加应试版的手写注释,也方便之后的ctrl cv。外加一句题外话
你啊,别想那么多,少年,反正这个世界本来就已经很疯狂了。
最小生成树
农夫约翰修光纤

经过之前的总结,我们可以确定其中考察的是prim和krustra算法的应用,直接使用模板思维。
先使用prim算法,也就是点点相连,将外边的点长加入进去
- 第一步就是存数据,有跟多种放法,可以使用矩阵表,也可以使用上下三角矩阵压缩,因为这个是无向图,完全对称的,也可以时候矩阵链表,只不过结构在调用的时候比较麻烦,所以我们可以直接用矩阵存就行,要是选择了矩阵压缩,按照行为主列为辅的下三角就行,就是将二维数组变成一维数组,也许用聪明的脑瓜感觉会有存储冲突的情况,其实不然,这就是矩阵压缩的好处,极大减免了很多存储的空间,和在整体遍历的时候出现的问题。
- 第二步和topsort找出入度情况一样,这次我们面对的是长度,也就是weight,那么就要采用长度为主,prim的理论也就伪代码要求的是无穷大,一个一个距离代入,找合适的,然后把之前的遍历bug路径修改成最新的。先选择最弱的然后吞并加强之后再找其他的,苏秦张仪合纵连横之法,不过尔尔。
- prim代码的核心也就是st[]遍历和长度的覆盖问题、
呈上代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e2+10;
int g[N][N],dist[N],res=0;//存数据
int n,st[N];//遍历过的点就不踩了。
void prim(){
memset(dist,0x3f3f,sizeof(dist));
dist[0]=0;
for(int i=0;i<n;i++){
int t=-1;
for(int j=0;j<n;j++){
if(!st[j]&&(t==-1||dist[j]<dist[t]))t=j;
//t的存在也就是从起点开始,找最短的导入到路径圈里
}
st[t]=1;//天选之子,然后加入进去,同时把长度也搞进去
res+=dist[t];
for(int i=0;i<n;i++){
if(dist[i]>g[t][i]&&!st[i])dist[i]=g[t][i];
//一切的起点,覆盖路径,dist。
}
}
cout<<res;
}
int main(){
scanf("%d",&n );
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
scanf("%d ",&g[i][j]);
}
}
prim();
return 0;
}
Dijkstra算法应用,会发现和krustra算法趋向类似
int dist[N],st[N];
int e[N],h[N],ne[N],idx,w[N];
void add(int a,int b,int c){
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
int n,m;
void dijkstra(){
memset(dist,0x3f,sizeof(dist));
dist[1]=0;
for(int i=0;i<n;i++){
int t=-1;
for(int j=1;j<=n;j++){
if(!st[j]&&(t==-1||dist[j]<dist[t]))t=j;
}
st[t]=1;
for(int j=h[t];j!=-1;j=ne[j]){
int i=e[j];
dist[i]=min(dist[i],dist[t]+w[j]);//未访问的结点通过已经访问的结点到源点距离最小
}
}
}
int main(){
scanf("%d %d",&n,&m);
memset(h,-1,sizeof(h));
while(m--){
int a,b,c;
scanf("%d %d %d",&a,&b,&c);
add(a,b,c);
}
dijkstra();
会发现prim和dijkstra算法很类似但是他们也有区分点,
- 在图论中,Prim算法解决的问题是连通无向有权图中最小生成树问题,而Dijkstra算法解决的问题是源点到目标点的最短路径问题。
- 两个算法在添加新结点时,都是选择“距离最短”的结点加入集合,但是Prim算法中,“距离最短”是指未访问的结点到已经访问的所有结点距离最小,即将已经访问的结点视为一个整体,将距离最小的结点加入到已访问的集合中;而在Dijkstra算法中,“距离最短”是指所有未访问结点(通过已访问的结点)到源点距离最小。
- 在Prim算法中,数组元素dis[i]表示未访问结点i到已访问结点集合的最短距离,所以此时需要len记录最短距离。而Dijkstra算法中,数组元素dis[i]表示未访问结点i到源点的最短距离。
默认正无穷是0x3f3f3f3f,图论里常用的审核该路径是否被更改过。
prim
for(int v = 0; v < n; v++){ //G[][]表示连通无向有权图,u表示新加入的结点。
if(!vis[v] && G[u][v] < dis[v]){
dis[v] = G[u][v];
}
}
dj
for(int v = 0; v < n; v++){
if(!vis[v] && G[u][v] + dis[u] < dis[v]){
dis[v] = G[u][v] + dis[u];
}
}
krustra算法

#include<bits/stdc++.h>
using namespace std;
const int M=1e5+10;//边的数量
const int N=5e4+2;//点的数量有图要求的倍数连接
struct Node{
int x,y,v;
bool operator<(const Node &A) const//重构//目的是进行边权由小到排序 {
return v<A.v;//就想struct 一个cmp一样的效果
}
}a[M];
int n,m,fa[N];//也可以直接用数组h ne e存
//并查集的基本操作,因为在加入新边之后会考察会不会形成闭环,就需要find寻根问祖
int Find(int x){
if(x==fa[x]) return x;
return fa[x]=Find(fa[x]);
}
//Kruskal算法
int Kruskal(){
for(int i=1;i<=n;i++) fa[i]=i;//初始化父节点
sort(a+1,a+1+m);//将边权排序
int ans=0,cnt=n;//ans记录最小生成树的值,cnt代表有多少个集合
for(int i=1;i<=m;i++){
int x=Find(a[i].x),y=Find(a[i].y);//找起点和终点所属的集合
if(x!=y){//若是不在一个集合
fa[x]=y;//进行合并操作
ans+=a[i].v;//加最小边权
--cnt;//总集合树-1
}
if(cnt==1) break;//如果最终只有一个集合,说明已经生成了最小生成树,就结束循环
}
if(cnt!=1) return -1;//如果不为一个集合,返回-1
else return ans;//否则返回最小生成树值
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)//存图操作
scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].v);
printf("%d",Kruskal());
}
拓扑排序
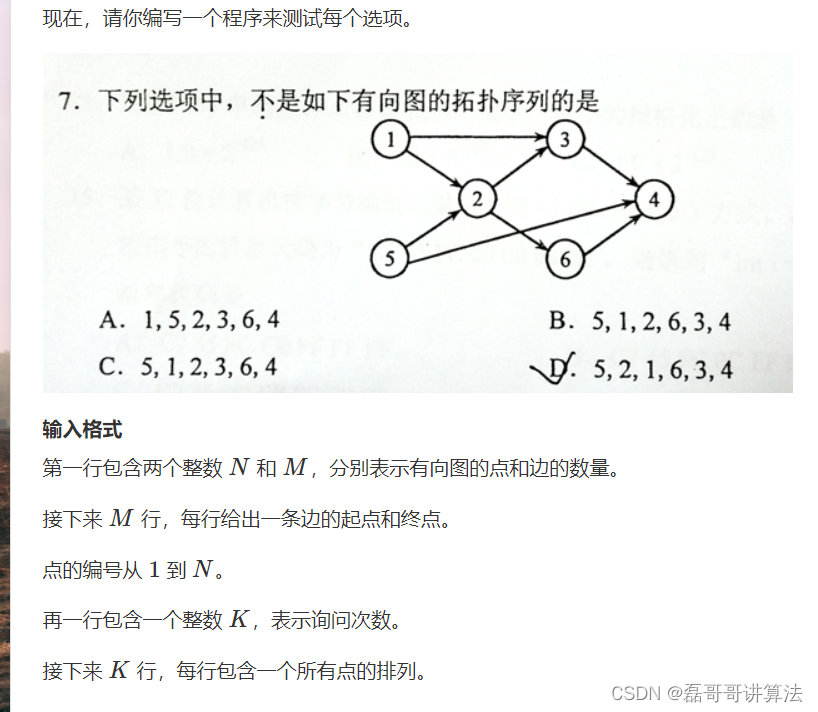
- 第一步拓扑图肯定是确定怎么存,直接使用结构体也可以,用数组的添加链表形式,因为是有向图,所以add要单项使用,add()框架记住cv加入的时候,b点的入度也要+1哦
- 拓扑就是出入度在每组demon资源每一个的query时,d[]就是获取入度,然后把能走的都走一遍
- 有DFS就是这个,另一种就BFS,队列最后是否为空
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
int e[N],h[N],ne[N],idx=1;
int n,m;
void add(int a,int b){
e[idx]=b;
ne[idx]=h[a];
h[a]=idx;
idx++;
}
int degree[N],d[N],query[N];
bool demon[N];
bool topsort(){
for(int i=1;i<=n;i++){
if(d[query[i]])return 0;
for(int j=h[query[i]];j!=0;j=ne[j])d[e[j]]--;
}
return 1;
}
int main(){
scanf("%d %d",&n,&m);
while(m--){
int a,b;
scanf("%d %d",&a,&b);
add(a,b);
degree[b]++;
}
int k;scanf("%d",&k);
for(int i=0;i<k;i++){
for(int j=1;j<=n;j++){
cin>>query[j];
d[j]=degree[j];
}
if(topsort())demon[i]=1;
else demon[i]=0;
}
for(int i=0;i<k;i++)
if(!demon[i])
cout<<i<<' ';
return 0;
}
//BFS队列法,topsort主要是出入度
public static boolean topsort(){
//将入度为0的点加入队列
for(int i = 1;i <= n;i ++){
if(d[i] == 0){
q[tail++] = i;
}
}
while(head < tail){
int headElement = q[head ++];//队首元素出队并记录
for(int i = h[headElement];i != -1;i =ne[i]){
int j = ele[i];
d[j] --;
if(d[j] == 0){
q[tail ++] = j;
}
}
}
return tail == n;//如果队列里元素个数等于节点个数,说明不存在自闭环,也就存在拓扑序列
}
Floyd

看要求,n点m边无向连通且有去掉后的重组,那么用Floyd的遍历更新更有优势
将Floyd算法理解就是内部i ~ n之间,用i~ k与k~j的重组最短距离
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int inf = 0x3f3f3f3f;
const int N = 55, M = 1600;
PII p[M]; // 保存边插入的顺序
int n, m, k, T, f[N][N], init[N][N];
void floyed(){
for (int v = 1; v <= n; ++v){
f[v][v] = 0;
for (int i = 1; i <= n; ++i){
for (int j = 1; j <= n; ++j) f[i][j] = min(f[i][j], f[i][v] + f[v][j]);
}
}
}
int main()
{
cin >> T;
while (T--)
{
memset(init, inf, sizeof init);
cin >> n >> m >> k;
for (int i = 1; i <= m; ++i)
{
int a, b, c;
cin >> a >> b >> c;
p[i] = {a, b};
init[a][b] = c;
init[b][a] = c;
}
memcpy(f, init, sizeof f); // 回到初始状态为了一步删除操作
floyed();
printf("%d\n", f[1][n]);
memcpy(f, init, sizeof f);//因为Floyd后的数据已经被更改过了
for (int i = 1; i <= k; ++i)
{
// 删除第x次插入得边,注意从a->b, b->a都要删除,删除就是更新为inf
int x; cin >> x;
f[p[x].first][p[x].second] = inf;
f[p[x].second][p[x].first] = inf;
}
floyed(); // 再次佛洛依德
if (f[1][n] > inf / 2) puts("-1");
else printf("%d\n", f[1][n]);
}
return 0;
}
道路与航线
题源
acwing的题,自己摸出来怪麻烦的
就是将topsort dijkstra 连通图 spfa 堆优化都用了,以后敲代码认真点,找了半天bug原来是输在sizeof上。累了
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e6 + 10;
int h[N], ne[N], e[N], w[N], idx;
int dist[N];
bool st[N];//基础三件套
int n, mr, mh, s;//航路区分
int id[N], bcnt;
int deg[N];//入度集
vector<int>block[N];//构建连通块
int q[N], hh = 0, tt = -1;//topsort的实现
//dijkstra小根堆优化
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c;
ne[idx] = h[a];
h[a] = idx++;
}
void dijskra(int block_id) {
priority_queue<PII, vector<PII>, greater<PII>>heap;
for (int u : block[block_id]) {
heap.push({ dist[u],u });
}
while (heap.size()) {
PII t = heap.top();
heap.pop();
int u = t.second;
if (st[u])continue;
st[u] = true;
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (dist[j] > dist[u] + w[i]) {
dist[j] = dist[u] + w[i];
if (id[j] == block_id)heap.push({ dist[j],j });//在块内就加入
}
if (id[j] != block_id && --deg[id[j]] == 0)q[++tt] = id[j];//外来块,就加入队列,作为桥梁链接新的区块
}
}
}
void dfs(int u) {
block[bcnt].push_back(u);
id[u] = bcnt;
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (!id[j])dfs(j);
}//划分了连通块
}
void topsort() {
memset(dist, 0x3f, sizeof(dist));
dist[s] = 0;
for (int i = 1; i <= bcnt; i++) {
if (!deg[i])q[++tt] = i;
}
while (hh <= tt) {
int t = q[hh++];
dijskra(t);
}
}
int main() {
scanf("%d %d %d %d", &n, &mr, &mh, &s);
memset(h, -1, sizeof(h));
for (int i = 0; i < mr; i++) {
int a, b, c;
scanf("%d %d %d", &a, &b, &c);
add(a, b, c), add(b, a, c);
}
for (int i = 1; i <= n; i++) {
if (!id[i]) {
++bcnt;
dfs(i);
}
}
for (int i = 0; i < mh; i++)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c), deg[id[b]]++;
}
topsort();
for (int i = 1; i <= n; i++)
{
if (dist[i] > 0x3f3f3f3f / 2) puts("NO PATH");
else printf("%d\n", dist[i]);
}
return 0;
}
堆合并
理解的话直接使用小跟堆就可以了,
实际上更要理解其实际应用流程,面临的习题是合并果子和荷马史诗,同样的划分类也有果子划分,属于DP全局里的,堆优化之后也是huffman编码的一种变形
主要是理解小跟堆里的up and down,类似于堆排序里的输出,只不过将输出的值进行存储变成新的数组添加进去在down头尾位置,和二叉排序树的添加没啥区别
priority_queue<PII,vector<PII>,greater<PII>> heap;
//小跟堆的荷马史诗,也可以手写代码的合并
while((n-1)%(m-1)){
heap.push({0ll,0});
n++;
} //解决并不是二叉树建huffman的情况下,保证可以构成满n叉树的数据处理
void up(int x){
if(x==1)return ;
int y=x/2;
if(h[y]>h[x]){
swap(h[y],h[x]);
up(y);
}
}//在基础构建的时候,添加一个数据用上浮up更快速搭建好数组模拟树。
void down(int x){
int t = x;
if (x * 2 <= idx && h[x * 2] < h[t])t = x * 2;
if (x * 2 + 1 <= idx && h[x * 2 + 1] < h[t])t = x * 2 + 1;
if (x != t) {
swap(h[x], h[t]);
down(t);
}
}
//在确定了大小之后的调整,也就是首尾交换位置从头down到尾的比较换位置
传统的数据结构
- 数据的逻辑结构, 线性结构和非线性结构
- 数据的物理结构,顺序结构 链表结构 散列结构 索引结构
- 数据结构的抽象层次
线性聚类 直接存取类(文件记录数组),顺序存储类(表栈队列),广义存储类(词典散列表)
非线性聚类 层次聚类比如数二叉树 堆,群聚集类 集合图 - 算法一个有穷的指令集,这些指令为解决某一特定任务规定了一个运算序列
数组
- 除第一个元素外,其他每一个元素都有一个且只有一个直接后继。
- 多项式
字符串
*strcpy char *strcpy(char *dest, const char *src) 把 src 所指向的字符串复制到 dest。参数dest – 指向用于存储复制内容的目标数组。参数src – 要复制的字符串。
``char a, sizeof(a)=1//不初始化的时候是1
char char2 = 'a';
cout << "size: " << sizeof(char2) << endl;//初始化只加入一个字符也是1
char char1;
if (char1 == '\0') //这样写法不严谨,这里只是为了验证
{
cout << "empty" << endl;
}
不可以将char形字符设置成一个空字符,这样的话程序会报错empty character constant ''是错的
强行空char的话可以char char1 = ' ';
构建空表伪代码
string:: string
ch=new char[maxlen+1];
if(!ch)exit(0);
ch[0]='\0';
最优二叉排序树
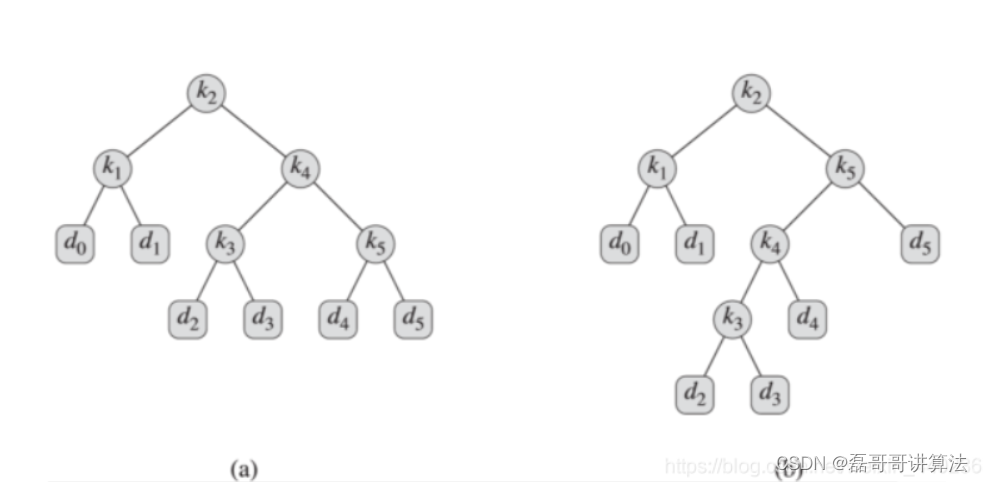
给定一个n个关键字的已排序的序列K=<k 1 ,k 2 ,…,k n >( 不失一般性,设k 1 <k 2 <…<k n ),对每个关键字k i ,都有一个概率p i 表示其搜索频率。根据k i和p i 构建一个二叉搜索树T,每个k i 对应树中的一个结点。若搜索对象x等于某个k i ,则一定可以在T中找到结点k i ;若x<k 1 或 x>k n 或 k i <x<k i+1 (1≤i<n), 则在T中将搜索失败。为此引入外部结点d 0 ,d 1 ,…,d n ,用来表示不在K中的值,称为伪结点。这里每个d i 代表一个区间, d 0 表示所有小于k 1 的值, d n 表示所有大于k n 的值,对于i=1,2,…,n-1,d i 表示所有在k i 和k i+1 之间的值。 同时每个d i 也有一个概率qi 表示搜索对象x恰好落入区间d i 的频率。

会出现两种可能的情况,那么我们要选择哪一种有效的呢



e[1..n+1,0..n]:用于记录所有e[i,j]的值。注:e[n+1,n]对应伪关键字d n 的子树;e[1,0]对应伪关键字d 0 的子树。
root[1..n]:用于记录所有最优二叉搜索子树的根结点,包括整棵最优二叉搜索树的根。
w[1..n+1,0..n]:用于子树保存增加的期望搜索代价,

画出三种表

w表底层用失败方框概率q填充,然后可以理解成三角求和依次往上累加
再向上就是qipi+w【i,j-1】
最难的e表也是最关键的部分,在构建e表的时候,所选择的最小e值合的同时也会同时保留成根表

R表
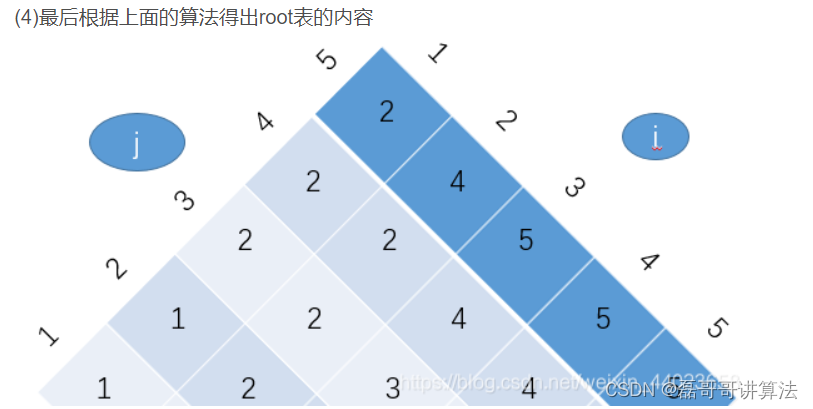
r表划分的是1 ~ N之间的点,所以
root [1,5]=2,那么2就是主root,将根植变成1 和2 和345,按照小于的在左,1是2的左子树
root [3,5]=5,那么2的右子树就是5. 5剩下3和4,
root [3,4 ]=4,4接在5的左子树
最后的3,3接在4的左子树
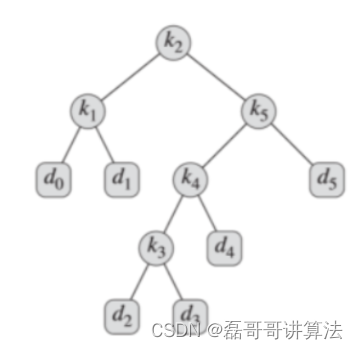
也就是一开始的图b
#include <iostream>
using namespace std;
const int MaxVal = 9999;
const int n = 5;
//搜索到根节点和虚拟键的概率
double p[n + 1] = { -1,0.15,0.1,0.05,0.1,0.2 };
double q[n + 1] = { 0.05,0.1,0.05,0.05,0.05,0.1 };
int root[n + 1][n + 1];//记录根节点
double w[n + 2][n + 2];//子树概率总和
double e[n + 2][n + 2];//子树期望代价
void optimalBST(double* p, double* q, int n){
//初始化只包括虚拟键的子树
for (int i = 1; i <= n + 1; ++i){
w[i][i - 1] = q[i - 1];
e[i][i - 1] = q[i - 1];
}
//由下到上,由左到右逐步计算
for (int len = 1; len <= n; ++len){
for (int i = 1; i <= n - len + 1; ++i){
int j = i + len - 1;
e[i][j] = MaxVal;
w[i][j] = w[i][j - 1] + p[j] + q[j];
//求取最小代价的子树的根
for (int k = i; k <= j; ++k){
double temp = e[i][k - 1] + e[k + 1][j] + w[i][j];
if (temp < e[i][j]){
e[i][j] = temp;
root[i][j] = k;
}
}
}
}
}
//输出最优二叉查找树所有子树的根
void printRoot()
{
cout << "各子树的根:" << endl;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
cout << root[i][j] << " ";
}
cout << endl;
}
cout << endl;
}
//打印最优二叉查找树的结构
//打印出[i,j]子树,它是根r的左子树和右子树
void printOptimalBST(int i, int j, int r) {
int rootChild = root[i][j];//子树根节点
if (rootChild == root[1][n]) {
//输出整棵树的根
cout << "k" << rootChild << "是根" << endl;
printOptimalBST(i, rootChild - 1, rootChild);
printOptimalBST(rootChild + 1, j, rootChild);
return;
}
if (j < i - 1)return;
else if (j == i - 1) {
if (j < r)
{
cout << "d" << j << "是" << "k" << r << "的左孩子" << endl;
}
else
cout << "d" << j << "是" << "k" << r << "的右孩子" << endl;
return;
}
else {
if (rootChild < r) {
cout << "k" << rootChild << "是" << "k" << r << "的左孩子" << endl;
}
else {
cout << "k" << rootChild << "是" << "k" << r << "的右孩子" << endl;
}
}
printOptimalBST(i, rootChild - 1, rootChild);
printOptimalBST(rootChild + 1, j, rootChild);
}
int main() {
optimalBST(p, q, n);
printRoot();
cout << "最优二叉树结构:" << endl;
printOptimalBST(1, n, -1);
}























 2119
2119











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










