基于GPUMD的NEP机器学习势函数—二氧化硅融化

Mr. Material

已于 2023-03-05 10:52:45 修改

阅读量3k

点赞数 4

分类专栏： Lammps实例教程—In文件详解文章标签： GPUMD Lammps

于 2022-12-03 21:09:09 首次发布

本文链接：https://blog.csdn.net/qq_43689832/article/details/128166431

版权

Lammps实例教程—In文件详解专栏收录该内容

33 篇文章 ¥19.90 ¥99.00

订阅专栏

超级会员免费看

本文介绍了基于GPUMD的NEP（核能量坡道）机器学习势函数在二氧化硅融化模拟中的应用。通过学习第一性原理计算结果，NEP势函数提高了模拟的精度。文章详细阐述了GPUMD的安装、NEP设置、Lammps中的配置，以及与经验势Tersoff的对比。提供了测试案例和代码获取方式。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

关注 $\color{Violet} \rm Mr.material\ ,$ $\color{red}{更}$ $\color{blue}{多}$ $\color{orange}{精}$ $\color{green}{彩}$ ！

主要专栏内容包括：
$\textbf{ \underline{\dag《LAMMPS小技巧》：}}$ 主要介绍采用分子动力学（ $L amm p s$ ）模拟相关安装教程、原理以及模拟小技巧（难度： $\bigstar$ ）
$\textbf{ \underline{\dag\dag《LAMMPS实例教程—In文件详解》：}}$ 主要介绍采用分子动力学（ $L amm p s$ ）模拟相关物理过程模拟。（包含：热导率计算、定压比热容计算，难度： $\bigstar$ $\bigstar$ $\bigstar$ ）
$\textbf{ \underline{\dag\dag\dag《Lammps编程技巧及后处理程序技巧》：}}$ 主要介绍针对分子模拟的动力学过程（轨迹文件）进行后相关的处理分析（需要一定编程能力。难度： $\bigstar$ $\bigstar$ $\bigstar$ $\bigstar$ $\bigstar$ ）。
$\textbf{ \underline{\dag\dag\dag\dag《分子动力学后处理集成函数—Matlab》：}}$ 主要介绍针对后处理过程中指定函数，进行包装，方便使用者直接调用（需要一定编程能力，难度： $\bigstar$ $\bigstar$ $\bigstar$ $\bigstar$ ）。
$\textbf{ \underline{\dag\dag\dag\dag\dag《SCI论文绘图—Python绘图常用模板及技巧》：}}$ 主要介绍针对处理后的数据可视化，并提供对应的绘图模板（需要一定编程能力，难度： $\bigstar$ $\bigstar$ $\bigstar$ $\bigstar$ ）。
$\textbf{ \underline{\dag\dag\dag\dag\dag\dag《分子模拟—Ovito渲染案例教程》：}}$ 主要采用 $\rm Ovito$ 软件，对 $\rm Lammps$ 生成的轨迹文件进行渲染（难度： $\bigstar$ $\bigstar$ ）。

$\color{red}{\textbf{ \underline{专栏说明（订阅后可浏览对应专栏全部博文）：}}}$
$\color{red} 注意：$ 如需只订阅某个单独博文，请联系博主邮箱咨询。 $\rm lammps\_materials@163.com$

$\spadesuit$ $\dag$ 开源后处理集成程序：请关注专栏《LAMMPS后处理——MATLAB子函数合集整理》
$\spadesuit$ $\dag$ $\dag$ 需要付费定制后处理程序请邮件联系： $\rm lammps\_materials@163.com$

势函数作为分子动力学模拟中最终要的输入之一，其准确性很大程度上决定了模拟结果的可靠性，传统经验势无法很好地描述所有现象，而能进行准确预测的基于第一性原理计算的分子动力学计算量非常大，无法进行大体系长时间的计算。因此最近兴起的机器学习势函数正是解决这一问题的有效工具，它可以通过对第一性原理的计算结果进行学习，通过这个方法得到的势函数具有接近第一性原理的计算精度。这里介绍一种基于GPUMD的NEP机器学习方法。 $\color{red} 只展示基本流程，因为数据集较少，结果准确性有待验证。$
感谢 $\color{red} \rm Dr.Maple$ 提供的测试案例

一、GPUMD安装及NEP设置

https://gpumd.org/installation.html

这里使用了https://www.nature.com/articles/s41524-022-00768-w中公开的数据集，其中每10个数数据取一个作为测试集，剩余作为训练集。

In文件：
version    4             #所使用nep版本
type       2  Si O       #元素种类数量，元素符号
cutoff     6  4          #径向和角度截断  A
neuron     50            #神经元数目
lambda_1   0.05          #第一类正则化参数
lambda_2   0.05          #第二类正则化参数
lambda_e   1.0           #能量权重因子
lambda_f   1.0           #应力权重因子
lambda_v   0.2           #位力权重因子
batch 10000              #full batch
population 50    
generation 300000        #迭代步数

在这里插入图片描述
将三个文件放在一个文件夹，然后通过以下命令运行得到结果。

/你的GPUMD路径/src/nep < nep.in | tee -a log.out

二、结果

运行完后可以得到如下文件（其中nep.txt就是机器学习得到的势函数）

在这里插入图片描述
可视化代码可以参考https://gpumd.org/tutorials/nep_tutorial.html
可以观察到能量和力都是相当准确的，其中位力不准确并未在这画出，想算准可能需要将一些不合适的结构剔除并且可以考虑将权重因子改为1。

在这里插入图片描述

三、Lammps计算

NEP势函数的配置
想要在lammps中使用NEP机器学习势函数需要进行配置，具体流程可参考https://mp.weixin.qq.com/s/fh0xRKxOZ3EIVtNpfJFwjQ，根据经验可直接将下图中的五个文件复制到lammps的src文件夹中使用make yes-user-nep, 再make mpi或你们所使用类型。
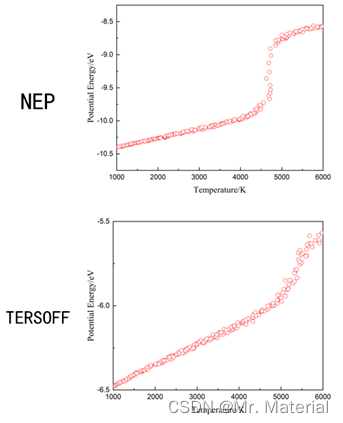
在这里插入图片描述