阵列信号相关处理算法 - 合集

目录

DOA估计算法（Direction Of Arrival）

数字波束形成DBF优化点

性质：

Capon算法（由于算法限制，通常使用时需要进行预处理）

性质：

Multiple Signal Classifier (MUSIC)

性质：

Root-MUSIC(一种MUSIC算法的变体，其中DOA估计通过找到多项式的根来执行)

性质：

空间平滑

---

DOA估计算法（Direction Of Arrival）

DOA 方法可以大致分为：二次预测（传统法）、线性预测和子空间法 ，如数字波束形成可分为二次法、前向后线性预测法和MUSIC子空间法。

参考书籍

《列阵信号处理的理论和应用》——张小飞、汪飞等

《列阵信号处理及MATLAB实现》——张小飞、陈华伟等

《现代数字信号处理》——王展、李双勋等

《最优阵列处理技术》——Harry L. Van Trees…

《The Difference Between Capon and MUSIC Algorithms》 Huiping Huang

一些DOA算法

问题公式化

假设天线位于远场。考虑一个由𝑀个传感器（天线阵元）组成的雷达系统，接收来自𝐾个源（目标）的信号，则接收到的信号可以表示为：

在一些优化权重算法中（如DBF、Capon）需要考虑传感器的加权输出。

这种情况下的传感器输出的加权线性组合可以表示为：

传感器列阵输出的功率𝑃(𝜔)可以表示为：

数字波束形成DBF优化点

DBF通过优化权值向量，使特定方向的输出功率最大化，最有权向量由下式给出：

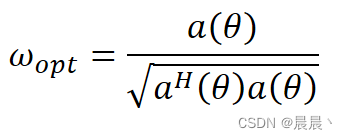
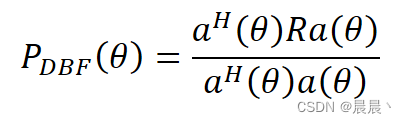
性质：

DBF只需要计算接收数据向量的协方差矩阵𝑅 ，计算复杂度较低。通过在期望的间隔内建立一个等间距角度的转向向量，谱搜索后则可以得到与最大功率相对应的角度作为DOA

但DBF无法分辨密集目标，不过它可以作为第一步来缩小高分辨率方法的目标范围，如先进行初步角度搜索，然后再进行精细搜索。

Capon算法（由于算法限制，通常使用时需要进行预处理）

Capon 算法旨在为从特定方向到达的信号保持恒定增益，同时赋予噪声较小的权重 。 它是最大似然法的替代算法，用于求解阵列的最小方差无失真响应 (MVDR)，从而使信干比最大化。 优化问题可以表示为： 

得到的最佳权重向量为：  

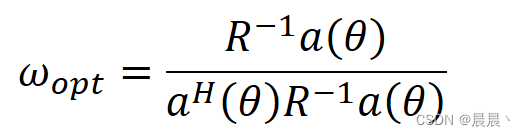
将最优权重向量带入方程。Capon功率为：

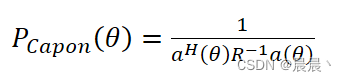
性质：

Capon 方法在分辨紧密相邻的目标方面为 DBF 提供了卓越的性能 ，此外，主要计算是从数据中确定逆协方差矩阵，这使得它在许多需要高分辨率的情况下非常有吸引力。还值得注意的是，Capon 和 DBF 都不需要事先了解信号源的数量，可以同时估计源信号的 DOA 和功率。

Capon 分离多个目标的能力仅受 SNR 和接收器阵列大小的限制，这是大多数高分辨率 DOA 方法的常见限制。

Capon 方法的缺点在于需要稳定计算，确定近奇异协方差矩阵的逆矩阵并非易事，尤其是在接收信号因噪声和杂波而劣化的汽车应用中。由于天线的孔径有限，如果没有某种形式的方法作为预处理的一部分，就无法可靠地计算协方差矩阵。然而，计算协方差矩阵的这个障碍并没有阻止 Capon 的使用。当然，如上所述，必须应用一些预处理技术

Multiple Signal Classifier (MUSIC)

MUSIC 采用子空间法来解决 DOA 估计问题 ，它利用特征分解作为主要工具。 特征分解背后的理论可以在文献

（Golub, G.H., Van Loan, C.F.: Matrix Computations, 3rd edn. Johns Hopkins University Press,
Baltimore, MD (1996)）中找到，在这里，我们给出要点。 子空间方法背后的主要假设是信号和噪声子空间是正交的，则使用正交性原理，可以计算伪谱，D 协方差矩阵可以分为信号和噪声分量。

性质：

MUSIC 算法是DOA估计的高分辨率技术之一。 它能够可靠地从严重劣化的接收信号中分辨出角度间隔低至 1° 的目标，伪谱中的杂散峰值非常少。 由于 MUSIC 计算接收信号的伪频谱，它不能用于估计信号源的功率。 对于功率估计，DBF 或 Capon 可以与 MUSIC 结合使用。 通过增加用于频谱估计的快拍数量，可以提高 MUSIC 分离多个目标的能力。

尽管具有高分辨能力，但 MUSIC 需要事先了解信号子空间的大小，另外还取决于需要高计算复杂度的特征分解。

Root-MUSIC(一种MUSIC算法的变体，其中DOA估计通过找到多项式的根来执行)

性质：

Root-MUSIC 具有与 MUSIC 相似的性能。 在某些需要考虑相位噪声的情况下，Root-MUSIC可以提供更好的性能。 与其他子空间算法一样，仍然需要提前知道目标源的数量。 在噪声和杂波严重的情况下，根的大小可能会远离单位圆，从而难以得到取感兴趣的根。

空间平滑

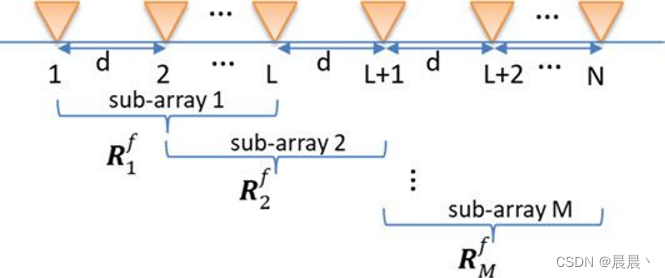
上述算法可以看出，协方差矩阵𝑅的估计是 DOA 估计过程的关键。 校正矩阵的大小由接收数据向量的大小决定，而向量大小又取决于接收天线阵列的长度。

对于基于特征的算法，DOA 估计只有在协方差矩阵是非奇异的情况下才有可能，这意味着信号是非相干或不相关的。 相干性的来源是由于多径等自然传播特性，也可能是干扰等人工信号的结果。 用于去相关信号的一种方法是空间平滑（SS）。

空间平滑是通过首先将天线阵列从可以计算的平均协方差矩阵划分为子阵列来实现的。 假设数组可以划分为𝑀个子数组，并将每个子数组计算的协方差矩阵表示为

上标表示正向计算，即增加元素所示，我们可以使用以下表达式计算协方差矩阵。