xgboost基本思想、节点分裂与公式详解

一、简单理解xgboost基本思路
xgboost融合了集成的思想，是n棵树模型的融合。比如下图，首先生成tree1模型，再生成tree2模型，然后再把这两个简单的模型最终得分累加起来，作为对应的数据的预测得分。
如下图的判断一个人是否爱玩游戏，男孩在tree1这边的树模型，从叶子结点可知得分是2，在tree2模型可知得分是0.9.则男孩的累积得分是2.9。（实际模型中还可根据情况进行加权累积）。老爷爷这个角色也同理，在tree1得分为-1，在tree2得分为0.9，累积得分0.1。
而tree1生成1和tree2则是通过不同的属性划分形成的树，如tree1是有age、is male 这两个属性进行的划分；tree2是根据 use computer daily这个属性进行的划分。

二、属性节点如何分裂，如何将一堆数据划分为左右子树？
目标函数如下（公式推理后续做解释）
该目标函数即是通过损失函数的求导，使导数为0，取得目标函数极值点后求得的目标函数。

5个数据对象：【男孩 女孩 妈妈 奶奶 爷爷】
先通过age这一属性进行划分。
case1：男孩，女孩划分在一边成为左子树，其余的划分在另一边为右子树。
case2：男孩，女孩，妈妈划分在一边成为左子树，其余的划分在另一边为右子树。
则此时根据划分前后目标函数的增益值进行决定划分如何进行划分（即划分的年龄age应该是小于多少划在一边），增益值越大，则划分越准确（有点类似决策树的信息增益和基尼系数增益）。

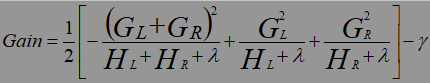
Gain=Obj（L+R）- Obj（L）- Obj（R）
其中G为损失函数的一阶导函数，H为损失函数的二阶导函数。公司中的y则是加入新叶子节点引入的复杂度代价。与Obj目标函数中的y有所不同（对于y此点没太明白）

三、公式详解
1、假设损失函数为均方误差L

由于是集成的算法，所以预测的分数必须是K棵树模型的累加。fk（xi）代表这一棵树模型。

在此我们目标是求得最优函数解，即最小化误差的期望值。如下：

2、树模型的加入

对于每一个树模型ft(x)

而叶子结点数越多，模型容易过拟合，所以指定了一个惩罚项Ω（ft）。T为叶子结点的数量，y为惩罚的力度，入为自设定参数。

将目标函数才分为前t-1棵树的状态加上新的树模型（ft）。constant为计算过程中产生的所有常数项。

用均方误差公式作为损失函数代入，此处的前t-1棵树模型的预测分数的平方由于是常数项，所以直接被融合到const中。化简得如下：

而我们的目标就是使得标中的残差最小化。

3、目标函数的优化
在此运用泰勒展开式，ft（xi）视为△x，则gi为损失函数的一阶导，hi为损失函数的二阶导。Ω（ft）为前面提到的正则项，防止叶子结点过多导致过拟合问题。由于在加入第t棵树的时候，前t-1棵树模型不变化，故在此前t-1棵树模型的计算结果为一个常数项目，所以将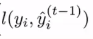直接去掉。

4、统一将样本上的遍历方法转换为叶子结点的遍历，如一个样本有5个数据对象：【男孩 女孩 妈妈 奶奶 爷爷】，左子树两个对象存放在一个叶子结点，右子树三个对象存放在一个叶子结点，那么部分遍历n（即5）个样本的就转化为遍历T（即2）个叶子结点。
w和q（xi）分别为对应的权重和预测值。

n代表着样本的数量，T代表着当前的第 t 棵树模型的叶子结点数量。
**tip：**下式代表着第 Ij 个叶子结点中所有的样本的一阶导之和

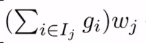
5、最终求解
进一步简化目标函数

对目标函数求偏导，使导数为0，求得Wj的值代回目标函数得到目标函数最终优化表达式。而Gj、Hj则得靠指明损失函数后求得对应的一阶导和二阶导。（可以直接算得）

最终目标函数如下，改分数越小，代表着整个数的结构越好，划分效果越好。

来一个例子看看如何计算目标函数得分值

接着便是节点分裂的问题了，选择目标分数值增益值大的作为划分点，进行优化。

资源来源：https://www.bilibili.com/video/BV1Ks411V7Jg?p=4