【Verilog学习日常】—牛客网刷题—Verilog企业真题—VL75

求最小公倍数

描述

       设计一个时序电路，输入2个无符号数,位宽可以通过参数DATA_W确定，输出这两个数的最小公倍数和最大公约数。

模块的接口信号图如下：

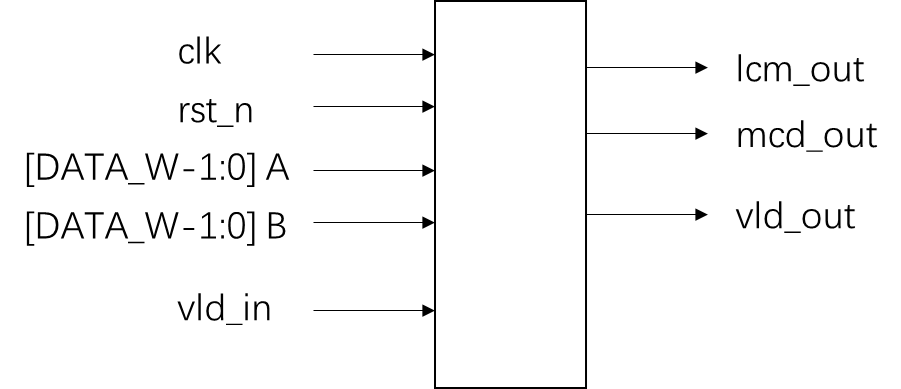
要求使用Verilog HDL语言实现，并编写testbench验证模块的功能。

输入描述：

clk:：时钟信号

rst_n：复位信号，低电平有效

A：输入信号，位宽可以通过DATA_W指定

B：输入信号，位宽可以通过DATA_W指定

vld_in：输入数据有效的指示信号

输出描述：

lcm_out：输出最小公倍数

mcd_out：输出最大公约数

vld_out：输出数据有效的指示信号

 解题思路

对于最小公倍数和最大公约数的求解，一般使用辗转相除法计算得到最大公约数，再利用两数的乘积除以最大公约数得到最小公倍数；

---

辗转相除法

例1：以被除数A = 33，除数B = 6为例：

①A/B = 33 / 6，商为5，余数为3；

②当上一步余数不等于0时，将①中的除数作为被除数，①中的余数作为除数；即6/3，商为2，余数为0，该式的除数3即为33和6的最大公约数；

被除数	除数	商	余数
33	6	5	3
6	3	2	0

例2：以被除数A= 35，除数B = 4为例：

被除数	除数	商	余数
35	4	8	3
4	3	1	1
3	1	3	0

当余数为0时，其对应的除数即为最大公约数；

通过以上两个例子，我们可以发现，辗转相除法的整个过程可以被分为两个状态（状态1：余数≠0；状态2：余数＝0）

更相减损术

更相减损术的算法内核与辗转相除法一致；将差和减数之间进行减法运算；

当差大于减数时，差作为下一轮被减数，减数仍然为下一轮减数；

当差小于减数时，差作为下一轮减数，减数则作为下一轮被减数；

例1：以被减数A = 33，减数B = 6为例：

被减数	减数	差
33	6	27
27	6	21
21	6	15
15	6	9
9	6	3
6	3	3
3	3	0

例2：以被减数A= 35，减数B = 7为例：

被减数	减数	差
35	7	28
28	7	21
21	7	14
14	7	7
7	7	0

同样的，使用有限状态机时，同样可以分为两个状态（状态1：差≠0（即更相相减阶段）；状态2：差＝0（即最终得出MCD的阶段））

代码详解

我们设置以下三个状态：

状态1——IDLE：A、B的初始化阶段；（即A和B还未开始运算）

当输入有效时（即vld_in = 1）时，进入迭代相减阶段（S1）；

代码如下：

        IDLE: begin
            if (vld_in) begin
                a_t <= A;
                b_t <= B;
                a_mul_b <= A * B;

                next_state <= S1; vld_out <= 1'b0;

            end
            else begin next_state <= IDLE;  vld_out <= 1'b0;end

        end

状态2——S1：A、B的更相相减阶段；

根据A、B的大小进行辗转相减；当差≠0时，next_state <= S1；当差=0时，next_state <= S2;

代码如下：

        S1: begin
            if (a_t > b_t)  begin  
                a_t <= a_t - b_t; b_t <= b_t; 
                next_state <= S1; vld_out = 1'b0; 
            end
            else if (a_t < b_t) begin 
                b_t <= b_t - a_t; a_t <= a_t;
                next_state <= S1; vld_out = 1'b0; 
            end
            else begin next_state <= S2; vld_out = 1'b0;  end
        end

状态3——S2：求MCD阶段

        S2: begin
            mcd_out_r <= a_t; //最大公约数 a_t == b_t
            vld_out <= 1'b1;
            next_state <= IDLE;
        end

完整代码

`timescale 1ns/1ns

module lcm#(
parameter DATA_W = 8)
(
input [DATA_W-1:0] A,
input [DATA_W-1:0] B,
input 			vld_in,
input			rst_n,
input 			clk,
output	wire	[DATA_W*2-1:0] 	lcm_out, //最小公倍数
output	wire 	[DATA_W-1:0]	mcd_out, //最大公约数
output	reg					vld_out
);

reg [DATA_W-1:0]   mcd_out_r;

reg [DATA_W-1:0] a_t,b_t;
reg [DATA_W*2-1:0] a_mul_b;

reg [1:0] current_state, next_state;
parameter [1:0] IDLE = 2'b00;
parameter [1:0] S1 = 2'b01; 
parameter [1:0] S2 = 2'b11;

always @(posedge clk or negedge rst_n) begin
    if (!rst_n) current_state <= IDLE;
    else        current_state <= next_state;
end

//更相减损术
always @(posedge clk or negedge rst_n) begin
    if (!rst_n) begin
        mcd_out_r = 'b0;
        vld_out = 1'b0;
    end
    else begin
        case(current_state) 
        IDLE: begin
            if (vld_in) begin
                a_t <= A;
                b_t <= B;
                a_mul_b <= A * B;

                next_state <= S1; vld_out <= 1'b0;

            end
            else begin next_state <= IDLE;  vld_out <= 1'b0;end

        end
        S1: begin
            if (a_t > b_t)  begin  
                a_t <= a_t - b_t; b_t <= b_t; 
                next_state <= S1; vld_out = 1'b0; 
            end
            else if (a_t < b_t) begin 
                b_t <= b_t - a_t; a_t <= a_t;
                next_state <= S1; vld_out = 1'b0; 
            end
            else begin next_state <= S2; vld_out = 1'b0;  end
        end
        S2: begin
            mcd_out_r <= a_t; //最大公约数 a_t == b_t
            vld_out <= 1'b1;
            next_state <= IDLE;
        end
        default: begin next_state <= IDLE;vld_out <= 1'b0; end
        endcase
    end
end

assign mcd_out = mcd_out_r;
assign lcm_out = a_mul_b / mcd_out;

endmodule