除法器设计学习笔记

爱斯基摩狗

已于 2023-12-14 10:19:43 修改

阅读量1.2k

点赞数 25

文章标签：学习笔记

于 2023-12-11 09:18:45 首次发布

本文链接：https://blog.csdn.net/qq_44783675/article/details/134309802

版权

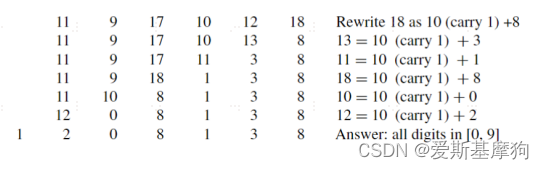
1. Paper-Pencil Division Algorithm

求解Q[2]，当Q[2]=1时，Q[2]*3=3>1，所以，Q[2]=0，且余数为1
求解Q[1]，余数为1，十位数为2，部分余数为12。当Q[1]=5时，Q[1]*3=15>12，当Q[1]=4时，Q[1]*3=12，刚好相等，余数为0
求解Q[0]，余数为0，个位为4，部分余数为4。当Q[0]=2时，Q[0]*3=6>4，故Q[0]=1,余数为1

2. 慢速算法

慢速算法通过循环等式，对余数R进行迭代：

$R_{j+1}=B\times R_j-q_{n-(j+1)}\times D$

R为部分余数
B为基，在基2算法中B为2
q为商

最终的余数 $R=R_{n}$ ，第一个部分余数 $R_{0}=N$

$\begin{aligned} &R=2R_{n-1}-q_0D=2R_{n-2}-2^1q_1D-q_0D=\cdots \\ &=2^nN-2^{n-1}q_{n-1}D-\cdots-2^1q_1D-q_0D \\ &=2^{n}N-QD \end{aligned}$

注：运算前，需要把 D 左移，得到结果时把 R 右移。

说明：（纯个人想法，不要看）

继续以124/3为例

1=124-3*0*10^2-3*4*10^1-3*1*10^0

按照这种方法，确定商位的同时，还要不断将Q*D除以基

若按照迭代方法，要获得3位商值，要将除数3乘以1000

第一次迭代：1240-3000*0，部分余数1240

第二次迭代将部分余数乘以基（以10为基）

12400-3000*4，部分余数400

第三次迭代部分余数乘以10

4000-3000*1，部分余数1000

运算完毕后，R3需要除以1000，即得到余数1，商041。

3. 恢复余数法(Restoring Division Algorithm)

对二进制，商只有0和1两种情况，若部分余数减去D为负数，则说明商为0，需要对部分余数进行恢复，即加D;若部分余数减去D为正数，则商为1。

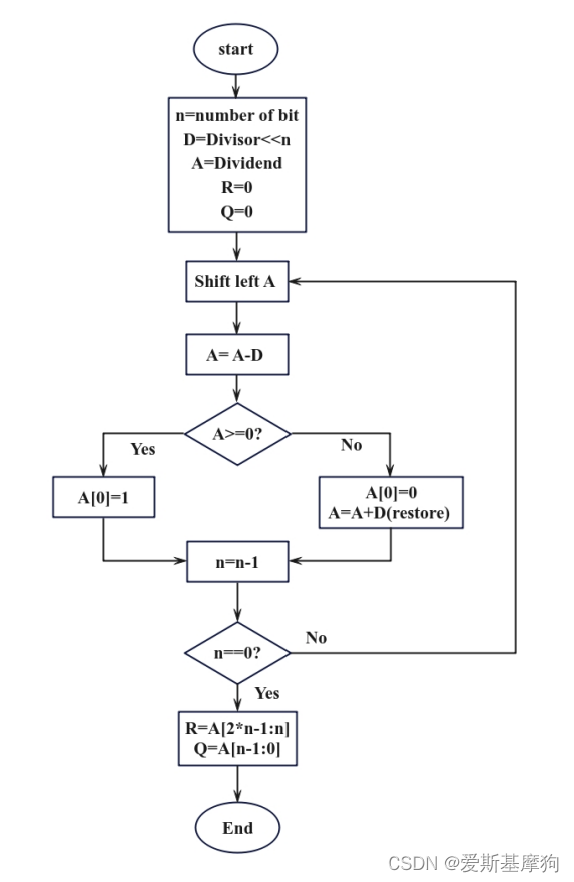
RISC-V 计算机硬件与接口描述（64位恢复余数除法）：

示例

求被除数N=10，除数D=3的商Q和余数R

10的二进制为1010

3的二进制为0011

初始化如下：

n = 4 D = 00110000 A = 00001010 R = 0000 Q = 0000

4.不恢复余数法

不恢复余数法商数的选择使用{-1，1}代替{0,1}，例如-3=（-1）（1）（1）（-1）

如果R-D<0，q取-1，R=2*R+D；R-D>0，q取1，R=2*R-D。不恢复余数法硬件实现上更有优势，每产生一个商的比特位只需要一次加或减操作，并且在减法操作后不需要进行余数恢复，执行的速度更快。

最后需要通过以下算式校准，将余数R转换为正数：

if R <0 then

Q=Q-1

R=R+DIvidend

end if

流程图

示例

求被除数N=10，除数D=3的商Q和余数R

10的二进制为1010 3的二进制为0011 -3的二进制为1101

初始化如下：

n = 4 D = 000110000

-D = 111010000（忽略低4位）

A = 000001010（预留一位进位）

R = 0000 Q = 0000

上述已经在计算过程中得到商值。商值也可通过商位转换获得，例如111（-1）1（-1）1（-1）

正数项：11101010

负数项：00010101

正数项减负数项：11010101

5. 冗余数字集

10进制的数字集{0,1,2,3,4,5,6,7,8,9}，含有10个非负数，为非冗余数字集。

如果数字集含有多于r个数字（包括0），则称为冗余。

一种特殊的冗余数字集Signed-Digit（SD）：

冗余因子

$\dfrac{1}{2}\leq\rho=\dfrac{a}{r-1}\leq1$

a=ceil(r/2)，，为最小冗余度，ceil为取整函数

a=r-1,为最大冗余度

a>r-1,则为过冗余度

数集间的转化：

6. SRT除法

SRT除法商使用了冗余表示，例如，在实现基 4 SRT 除法时，每个商位都是从五种可能性中选择的：{ −2, −1, 0, +1, +2 }。
商数的选择不必是完美的，后面的商数字可以纠正轻微的错误（例如，商数字对 (0, +2) 和 (1, −2) 是等价的，因为 0×4+2 = 1×4−2）。
冗余度允许仅使用少数几个被除数和除数的 MSB 数字来选择商位的数字，不需要全位宽的减法。

SRT除法相比与非恢复除法不同点：

对 divisor 进行归一化，简化运算流程，缩小硬件实现面积，在SRT的第一步进行；
商位的选择使用冗余表示，允许仅使用少数几位来选择，无需使用全位宽的减法，这一过程通常由 QDS (quotient digit selection) 查找表实现；
由于使用冗余表示，需要对结果进行转换，通常使用on-the-fly conversion进行实时的转换，而不用浪费额外的时钟周期;
divisor 归一化会对计算得到的 quotient 和remainder 值造成影响，同时 remainder 可能是负数，需要进一步处理。

7. On-the-Fly Conversion算法

On-the-Fly Conversion算法用于将冗余数字表示转换为常规表示的算法。上述将数字集{-1，1}转换至数字集{0，1}曾经介绍过，首先要将正负项分开，然后相减，此操作通过进位传播加法器进行。然而，这会将加法器的延时添加到总的操作时间中。SRT商位以逐位方式获得，On-the-Fly Conversion算法可以通过当前结果的两种条件形式进行即时转换（产生一位商数就即时转换出来），产生的总延时大致相当于一个进位保存加法器。

转换原理及过程：

以基2 SRT除法为例，把冗余数字集p转化为常规表示q，其中：

$p=\sum_{i=1}^{m}p_{i}2^{-i},\quad p_{i}\in\{-1,{0},1\}$

$q=-q_0+\sum_{i=1}^mq_i2^{-i},\quad q_i\in\{0,1\}$

On-the-Fly Conversion在p产生时便执行：

$q[k]=q[k-1]+p_{k}2^{-k}$

当p=-1时算法要求传播进位，例如：

$q_i,q_{i+1},\cdots,q_{k-2},q_{k-1}=1,0\cdots0,0$

pk=-1，需要考虑向高位借位：

$q_i,q_{i+1},\cdots,q_{k-2},q_{k-1},q_k=0,1,\cdots,1,1,1$

通过保留两种条件形式来避免进位的传播：

$q[k]=\begin{cases}A[k-1]+2^{-k}&\quad\text{if} \quad p_k=1\\\\A[k-1]&\quad\text{if} \quad p_k=0\\\\B[k-1]+2^{-k}&\quad\text{if} \quad p_k=-1\end{cases}$

其中：

$A\left[k-1\right]=-q_{0}+\sum_{i=1}^{k-1}q_{i}2^{-i}=q\left[k-1\right]$

$B[k-1]=A[k-1]-2^{-(k-1)}$

初始条件：

$\left.A\left[1\right]=\left\{\begin{matrix}+1/2&(0.1)&\text{if} \quad p>0&(p_1=+1)\\-1/2&(1.1)&\text{if} \quad p<0&(p_1=-1)\end{matrix}\right.\right.$

$\left.B[1]=\left\{\begin{matrix}+0&(0.0)&\text{if} \quad p>0&(p_1=+1)\\-1&(1.0)&\text{if} \quad p<0&(p_1=-1)\end{matrix}\right.\right.$

对于k>1：

$A\left[k+1\right]=\begin{cases}A\left[k\right]+2^{-\left(k+1\right)}&\quad\mathrm{if~}p_{k+1}=1\\A\left[k\right]&\quad\mathrm{if~}p_{k+1}=0\\B\left[k\right]+2^{-\left(k+1\right)}&\quad\mathrm{if~}p_{k+1}=-1\end{cases}$

$B[k+1]=\begin{cases}A\left[k\right]&\quad\text{if} \quad p_{k+1}=1\\B\left[k\right]+2^{-\left(k+1\right)}&\quad\text{if} \quad p_{k+1}=0\\B\left[k\right]&\quad\text{if} \quad p_{k+1}=-1\end{cases}$

示例：

对 $P=0.1101\bar{1}00\bar{1}1010\mathrm{}$ 进行转换

转换结果为q=0.110001111010

再比如，对 $P=0.\bar{1}0\bar{1}100\bar{1}1$ 进行转换

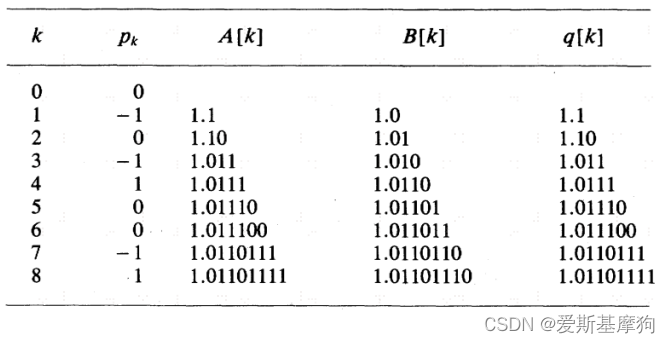
结果为q=1.01101111，为负数

基r转换：

$p=\sum_{i=1}^{m}p_{i}r^{-i},p_{i}\in\{-a,\cdots,0,\cdots,a\}\quad r/2\leq|a|\leq r-1$

转换后的商数：

$q=-q_{0}+\sum_{i=1}^{m}q_{i}r^{-i},\quad q_{i}\in\{0,\cdots,r-1\}.$

为保持算法特性，转化的广义表达为：

$\left.q[k]=\left\{\begin{array}{ll}A[k-1]+p_kr^{-k}&\quad\text{if } \quad p_k\geq0\\B[k-1]+(r-|p_k|)r^{-k}&\quad\text{if } \quad p_k<0\end{array}\right.\right.$

其中：

$A\left[k-1\right]=q\left[k-1\right]$

$B[k-1]=A\left[k-1\right]-r^{-(k-1)}$

初始条件：

$\left.A\left[1\right]=\left\{\begin{array}{ll}+p_1r^{-1}(0.p_1)&\quad\text{if} \quad p>0\\-|p_1|r^{-1}(1.(r-|p_1|))&\quad\text{if} \quad p<0\end{array}\right.\right.$

$\left.B[1]=\left\{\begin{array}{ll}+(p_1-1)r^{-1}(0.(p_1-1))^*&\quad\text{if } \quad p>0\\-(|p_1|+1)r^{-1}(1.(r-1-|p_1|))&\quad\text{if } \quad p<0\end{array}\right.\right.$

k>1:

$\left.A\left[k+1\right]=\left\{\begin{array}{ll}A\left[k\right]+p_{k+1}r^{-(k+1)}&\quad\text{if} \quad p_{k+1}\ge0\\B[k]+(r-|p_{k+1}|)r^{-(k+1)}&\quad\text{if} \quad p_{k+1}<0\end{array}\right.\right.$

$\left.B[k+1]=\left\{\begin{array}{ll}A[k]+(p_{k+1}-1)r^{-(k+1)}&\quad\text{if} \quad p_{k+1}>0\\B[k]+((r-1)-|p_{k+1}|)r^{-(k+1)}&\quad\text{if} \quad p_{k+1}\leq0\end{array}\right.\right.$

从基4冗余至二进制补码转换：

对基4冗余，将 $a=(a_{1},a_{0})$ 附加到A[k]，其中 $2a_{1}+a_{0}\in\{0,1,2,3\}$ ，将 $b=(b_{1},b_{0})$ 附加到B[k]。

$A\leftarrow\begin{cases}\text{Shift}A\text{with insert}(a_1,a_0)\quad&\text{if} \quad C_{SHA}=1\\\text{Shift}B\text{with insert}(a_1,a_0)\quad&\text{if} \quad C_{LDA}=1\end{cases}$

$B\leftarrow\begin{cases}\text{Shift}B\text{with insert}(b_1,b_0)&\quad\text{if} \quad C_{SHB}=1\\\text{Shift}A\text{with insert}(b_1,b_0)&\quad\text{if} \quad C_{LDB}=1\end{cases}$

对基4最小冗余度， $p_i\in\{-2,-1,0,1,2\}$ , 由以下符号和幅度代码表示：

a1、a0、b1、b0表示为：

$\begin{gathered} a_{1}=s+m_{1} \\ a_{0}=m_{0} \\ b_{1}=m_{0}^{\prime}m_{1}^{\prime}+sm_{1}^{\prime} \\ b_{0}=m_{0}^{\prime}. \end{gathered}$

$\begin{gathered} C_{LDA}=s \\ C_{SHA}=s^{\prime} \\ C_{LDB}=(s+m_{0}^{\prime}m_{1}^{\prime})^{\prime}=C_{SHB}^{\prime} \\ C_{SHB}=s+m_{0}^{\prime}m_{1}^{\prime}. \end{gathered}$

转换表：

8. 基2 SRT算法

商数选择（Quotient Digit Selection，QDS）函数

上述两种除法器部分余数迭代函数为：

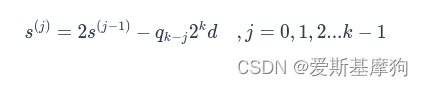
恢复余数法商值在{1，0}之间选择

不恢复余数法商值在{1，-1}之间选择

SRT算法对QDS函数选择进行了修改，商值在{1，0，-1}之间选择

SRT除法基本步骤

进行SRT除法时，首先要将 divisor 归格化至 [1/2，1），同时记录移位个数m，将dividend归格化至(x,1/2), 同时记录移位个数n
商位选择：根据部分余数，做简单的移位，然后与 1/2 做对比选择商位，在基2-SRT中，QDS 查找表比较简单，可以直接做判断实现；
迭代计算：根据选择的商位对余数做迭代运算，总的迭代次数为m-n；
实时转换 (on-the-fly conversion)：根据实时转换算法，对 Remainder 和 Quotient 的值做实时转换，将迭代中使用的冗余形式转换为2进制补码形式；
后处理：根据移位个数 m 对商值以及余数进行调整，例如，对于无符号运算，同时如果余数为负数，需要对余数加上 D，同时商值减去 ulp (unit of least precision, 通常是1)

示例：计算11/3=(3,2)，除数和被除数都是8比特，8'd11=00001011, 8'd3=00000011。

小数点置于最高位和最高位的下一位（即第八位和第七位之间），被除数有4个前导0，除数有六个前导零，将除数归格化至 [1/2，1），即左移五位，变为0.1100000；被除数归格化至(x,1/2)，可左移1位或两位，将被除数左移一位，变为0.0010110。迭代次数为除数移位数减去被除数移位数。每次确定商位，根据上述QDS函数需要对部分余数和除数进行比较，若二者位宽很大，硬件电路占用的面积就会很大。

将除数归格化至 [1/2，1），引入新的分界点-1/2和1/2来替代-d和+d：

$-d\leq-\frac12\leq2s^{(j-1)}<\frac12\leq d$

QDS更新如下：

$q_{k-j}=\begin{cases}1&\quad,2s^{(j-1)}\geq\frac12 \\0&\quad,\frac12>2s^{(j-1)}\geq-\frac12\\-1&\quad,2s^{(j-1)}<\frac12\end{cases}$

q的选择有三种情况：

1. 当2s[j-1]>=1/2（即0.1），则q值为1, 即最高两比特为0.1；

2. 当2s[j-1]<-1/2（即1.1），则q值为-1，即最高两比特为1.0；

3. 其他情况，q值为0；

即只要判断部分余数最高两比特就可得到商值，不需要将部分余数与全精度的除数进行比较。

示例：被除数x=69，除数d=10，求商q和余数rem

9. Roberson图与overlap

部分余数迭代式为：

$w_{j+1}=rw_j-dq_{j+1}$

假设rw(j)=x，w(j+1)=y，重写上式：

y = x – d*q

当q=0, y = x

当q=1, y = x – d

当q=2, y = x – 2d

…

根据不同的q值描绘出很多个y和x关系的直线

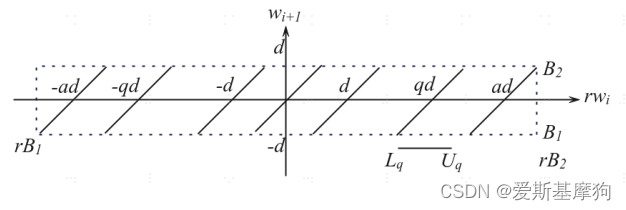
商q从数字集{-a,-a+1,…,-1,0,1,…,a-1,a}中取值，画出所有曲线，即是Roberson图。

对于QDS函数，其目的在于选择出商值q，而其收敛的条件为：

$B_{1}\leq w_{j-1}=rw_{j}-dq\leq B_{2}$

根据上图：

$\begin{aligned}Lq&=q*d+B_1\\Uq&=q*d+B_2\end{aligned}$

q取a和-a时，边界为：

$\begin{aligned}rB_1&=-a*d+B_1\\rB_2&=a*d+B_2\end{aligned}$

得：

$\begin{aligned}B_1&=-\rho d\\B_2&=\rho d\end{aligned}$

故：

$\begin{aligned}L_q&=(q-\rho)d\\U_q&=(q+\rho)d\end{aligned}$

对于任意的wj，为保证其至少有一个商值可以选择,则必须满足：

$U_{q-1}-L_q=(2\rho-1)d\geq0$

Overlap：即重合的区域

对于q：y = x – d*q

对于q-1：y = x – d*(q-1)

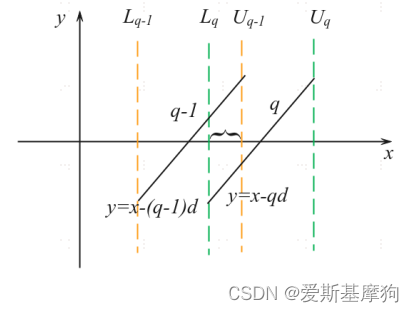
当x在橘色区域时，商的值可选为q-1

当x在绿色区域时，商的值可选为q

当x在交叠区域时，可选商值q-1和q

10. PD图

采用P替换掉rwj：

$B_{1}\leq P-Dq\leq B_{2}$

上文已推导：

$\begin{aligned} &B_{1}=-\rho D \\ &B_{2}=\rho D \\ &L_{q}=(q-\rho)D \\ & U_{q}=(q+\rho)D \\ &L_{q} \leq P\leq U_{q} \end{aligned}$

将上限Uq和下限Lq分别写成：

$\begin{aligned}P1&=(q-\rho)D\\P2&=(q+\rho)D\end{aligned}$

以最小冗余度基4 SRT部分PD图区域为例，其商数集为{-2，-1,0，1,2}，最大值a为2，基r=4

$\rho=\frac{a}{r-1}=\frac23$

当q=0时

$\begin{aligned}P1&=\left(0-\frac23\right)D=-\frac23D\\P2&=\left(0+\frac23\right)D=\frac23D\end{aligned}$

当q=1时

$\begin{aligned}P1&=\left(1-\frac23\right)D=\frac13D\\P2&=\left(1+\frac23\right)D=\frac53D\end{aligned}$

当q=2时

$\begin{aligned}P1&=\left(2-\frac23\right)D=\frac43D\\P2&=\left(2+\frac23\right)D=\frac83D\end{aligned}$

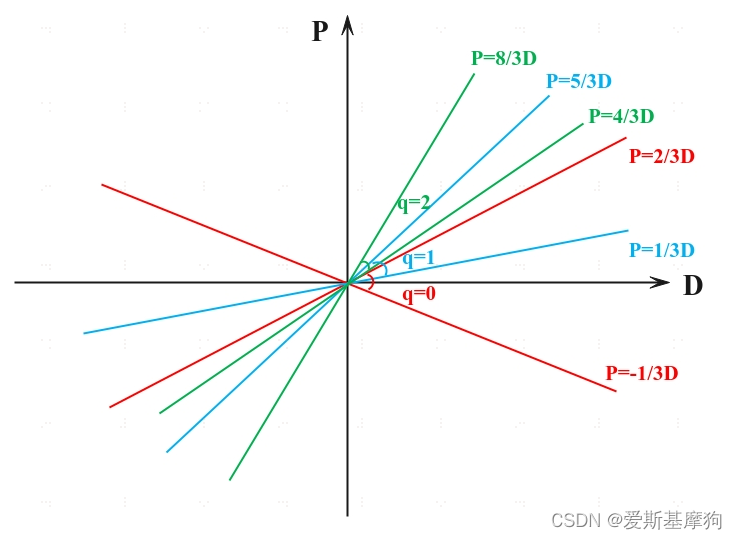
11 基4-SRT除法

基4的SRT算法使用每2比特进行迭代，迭代的次数由移位的比特来确定。使用m表示除数移位的比特，n表示被除数移位的比特，，总的迭代次数是(m-n)/2，并且，m和n必须同样是偶数或者同样是奇数，否则会对迭代过程造成影响。

以23/5为例，23规格化为00.0010111，没有进行移位；5规格化为00.1010000，左移4位，故基4-STR迭代两次。

根据上述PD图，可构建QDS表，可通过检查少数几个比特来确定商值。

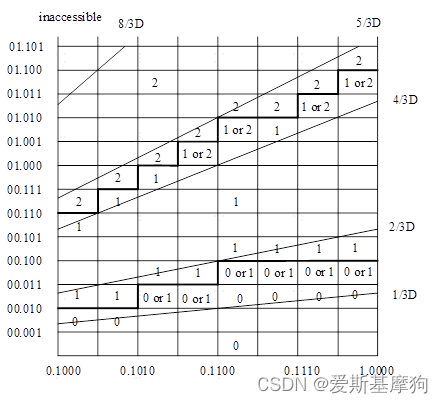
例如，D=0.1010，P=00.011，应选择1作为商值，D=0.1010，P=00.010，应选择0。

图中标注了“0 or 1”或者“1 or 2”的意味着该处的商值可以选择0也可以选择1。

基4中的11是基2中的0101，这里没有负数项，无需做减法。

负数情况：23/-5=(-4,3)

-5的补码为11.0000011，左移4位11.0110000，被除数00.0010111

商值选择时，需要把D转换为正数（原码）的形式，0.1010，然后使用负数的QDS表进行查表

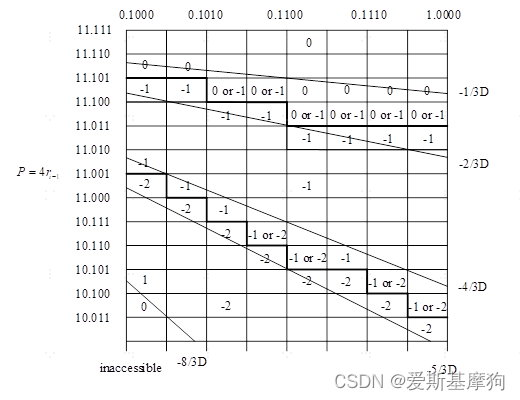
与正数的QDS表不同，不再选择左下角的点，而是左上角的点，例如，如果D=0.1010,P=11.101，我们应该选择-1作为商值。

示例：23/-5=(-4，3)

除数是负数，在后处理过程中，q应该加上1，R应该减去D（负数）。

示例： -23/5=(-5,2)

爱斯基摩狗

关注

25
点赞
踩
18

收藏

觉得还不错? 一键收藏
9
评论
除法器设计学习笔记

使用m表示除数移位的比特，n表示被除数移位的比特，，总的迭代次数是(m-n)/2，并且，m和n必须同样是偶数或者同样是奇数，否则会对迭代过程造成影响。R-D>0，q取1，R=2*R-D。不恢复余数法商数的选择使用{-1，1}代替{0,1}，例如-3=（-1）（1）（1）（-1）以最小冗余度基4 SRT部分PD图区域为例，其商数集为{-2，-1,0，1,2}，最大值a为2，基r=4。例如，D=0.1010，P=00.011，应选择1作为商值，D=0.1010，P=00.010，应选择0。
复制链接

扫一扫