Slater‘s condition (Slater条件)

Slater’s condition

Slater’s condition是优化问题中的一个重要条件，它通常与约束优化相关。Slater’s condition指的是在一些特定条件下，可以确保优化问题的强对偶性成立。

假设我们有一个带有约束条件的优化问题，通常表示为：

[ $\text{minimize}f(x)$ ]
[ $\text{subject to}{g}_i(x)\le 0,i=1,2,...,m$ ]
[ $\text{and}{h}_j(x)=0,j=1,2,...,p$ ]

Slater’s condition的表述是：如果存在一个点 ($x$)，使得不等式约束 ($g_i(x)<0$) 对所有的 ($i$) 成立，并且所有的约束函数 ($g_i(x)$) 和 ($h_j(x)$) 是凸的，那么强对偶性就成立。这意味着原始问题与其对偶问题的最优解是相等的。

Slater’s condition在优化理论中是一个很重要的条件，它为证明优化问题的强对偶性提供了一种方法。

强对偶性与弱对偶性

在优化理论中，对于一个给定的原始优化问题（primal optimization problem）和其对应的对偶问题（dual optimization problem），存在两种对偶性，即强对偶性（strong duality）和弱对偶性（weak duality）。

1. 强对偶性（Strong Duality）：

   • 强对偶性是指对于原始问题和对偶问题，它们的最优值相等，即原始问题的最优值等于对偶问题的最优值。形式化地，对于原始优化问题 ($P$) 和对偶优化问题 ($D$)，如果满足：
     [ ${\text{min}}_{x}f(x)={\text{max}}_{\lambda ,\nu }g(\lambda ,\nu )$ ]
     则称原始问题 ($P$) 与对偶问题 ($D$) 具有强对偶性。

2. 弱对偶性（Weak Duality）：

   • 弱对偶性是指对于原始问题和对偶问题，它们的最优值满足一个不等式关系。具体来说，对于任何可行解 ($x$) 和对偶可行解 ( $(\lambda ,\nu )$ )，原始问题的最优值 ($f^{\ast }$) 和对偶问题的最优值 ($g^{\ast }$) 满足：
     [ $f^{\ast }\ge g^{\ast }$ ]
     弱对偶性是一个更弱的条件，它对问题的性质进行了限制，但并不要求最优值的相等。

强对偶性是更强的结果，它意味着原始问题与对偶问题具有完全相同的最优值，而弱对偶性则是一个更普遍的结果，只要求最优值之间满足一个不等式关系。

拉格朗日对偶函数

拉格朗日对偶函数是优化理论中与拉格朗日对偶问题相关的重要概念。在优化问题中，拉格朗日对偶函数是原始优化问题的拉格朗日乘子（Lagrange multipliers）的函数。它是关于拉格朗日乘子的函数，而不是关于原始变量的函数。

考虑一个带有约束条件的优化问题：

[ $\text{minimize}f(x)$ ]
[ $\text{subject to}{g}_i(x)\le 0,i=1,2,...,m$ ]
[ $\text{and}{h}_j(x)=0,j=1,2,...,p$ ]

其中 ($f(x)$) 是目标函数，($g_i(x)$) 是不等式约束，($h_j(x)$) 是等式约束。

通过引入拉格朗日乘子 (${\lambda }_i\ge 0$) 和 (${\nu }_j$)，我们可以构建拉格朗日函数（Lagrange function）：

[ $L(x,\lambda ,\nu )=f(x)+{\sum }_{i=1}^m{\lambda }_i{g}_i(x)+{\sum }_{j=1}^p{\nu }_j{h}_j(x)$ ]

然后，拉格朗日对偶函数（Lagrange dual function）是将拉格朗日函数关于原始变量 ($x$) 最小化得到的结果，即：

[ $g(\lambda ,\nu )={\inf }_{x}L(x,\lambda ,\nu )$ ]

拉格朗日对偶函数是拉格朗日函数的下确界。它是关于拉格朗日乘子 ($\lambda$) 和 ($\nu$) 的函数，用于定义拉格朗日对偶问题，通过最大化对偶函数来寻找原始优化问题的下界。

第一阶优化条件（First-order optimality conditions）

第一阶优化条件（First-order optimality conditions）是优化问题的一组必要条件，用于确定潜在的最优解。这些条件提供了关于函数的导数或梯度的信息，以确定潜在最优解的位置。在最小化或最大化函数的过程中，第一阶优化条件通常被用来寻找驻点（stationary points）或者局部最优解（local optimal solutions）。

一般来说，第一阶优化条件包括以下情况：

1. 一阶导数为零：对于最小化问题，如果一个点是局部最小值，则其梯度（或导数）为零。对于最大化问题，类似地，梯度（或导数）的相反方向为局部最大值点，因此等于零。数学上，这可以表达为：

[ $\nabla f(x^{\ast })=0$ ]

其中，( $x^{\ast }$ ) 是函数的局部最优解。

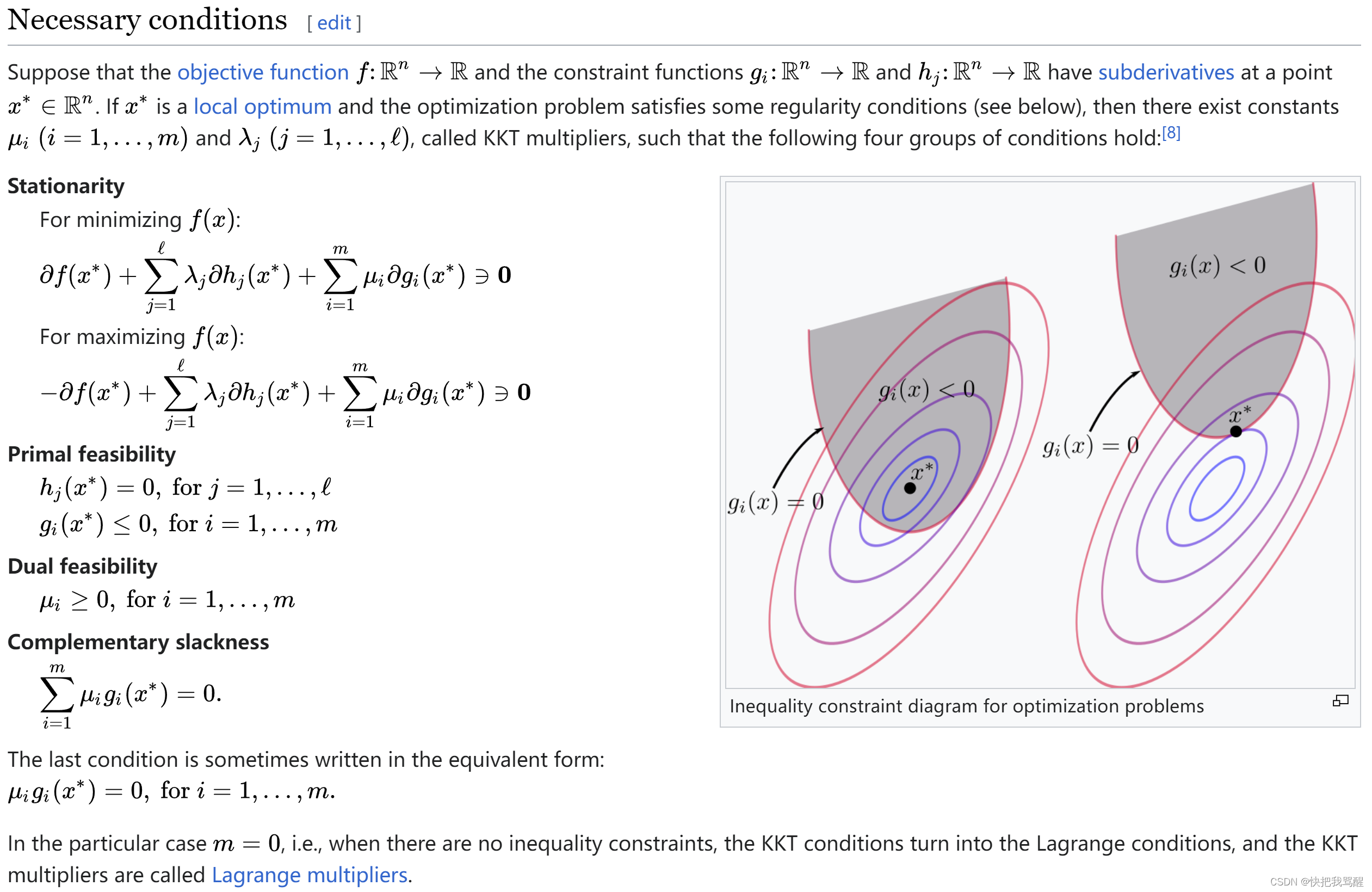
2. KKT条件：Karush-Kuhn-Tucker（KKT）条件是一组用于非线性规划问题的约束优化条件，它结合了目标函数和约束条件的梯度。对于约束优化问题，满足KKT条件是局部最优解的必要条件。

KKT条件包括：

• 原始可行性条件（Primal feasibility conditions）：即约束条件 ( $g_i(x)\le 0$) 和 ( $h_j(x)=0$ ) 在局部最优解点 ( $x^{\ast }$ ) 下成立。
• 对偶可行性条件（Dual feasibility conditions）：拉格朗日乘子非负性要求 ( ${\lambda }_i\ge 0$ )。
• 梯度乘子条件（Gradient multiplier conditions）：拉格朗日函数的梯度满足 ( ${\nabla }_{x}L(x^{\ast },{\lambda }^{\ast },{\nu }^{\ast })=0$ )。

这些条件通常在最优化问题的求解中用于确定潜在的最优解，它们提供了解的必要条件。

维基百科