Rasterization

Representation of pixels 像素的表示方法
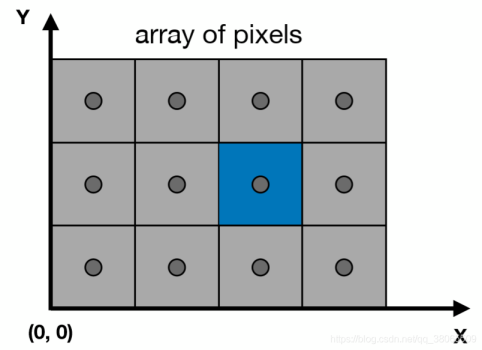
屏幕中的每一个像素点我们都用整数坐标进行表示,最大最小值与分辨率相对应,考虑到每个像素都有一定的面积,我们定义(x+0.5,y+0.5)为该(x,y)像素的中心
triangle Rasterization 三角形光栅化
三角形是最基本的多边形,大部分的模型都是用一个个三角形面表示,且任意的其它多边形其实都可以转化成多个三角形的形式
例如:

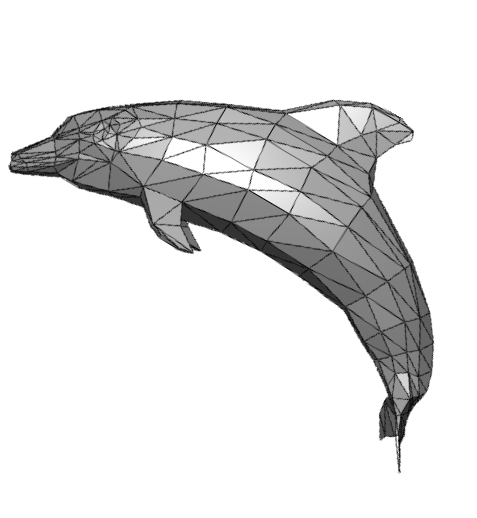
对三角形进行光栅化
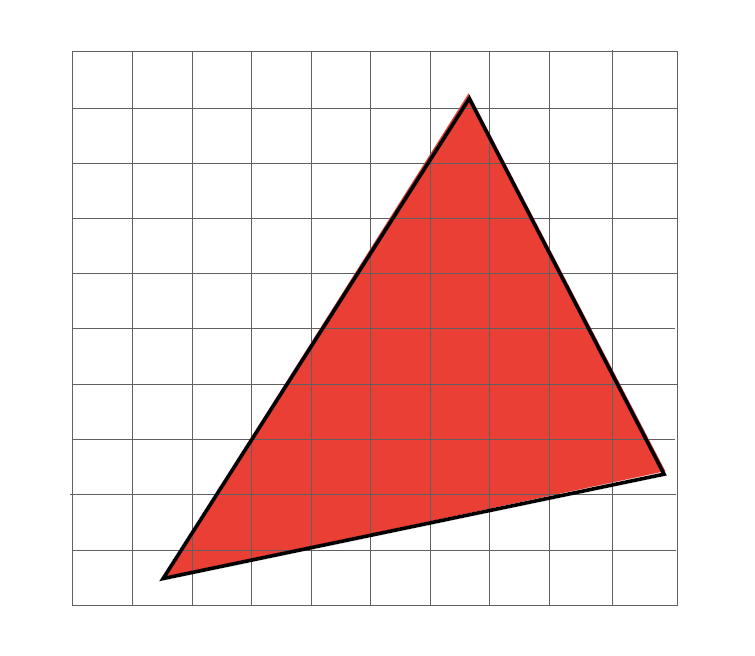
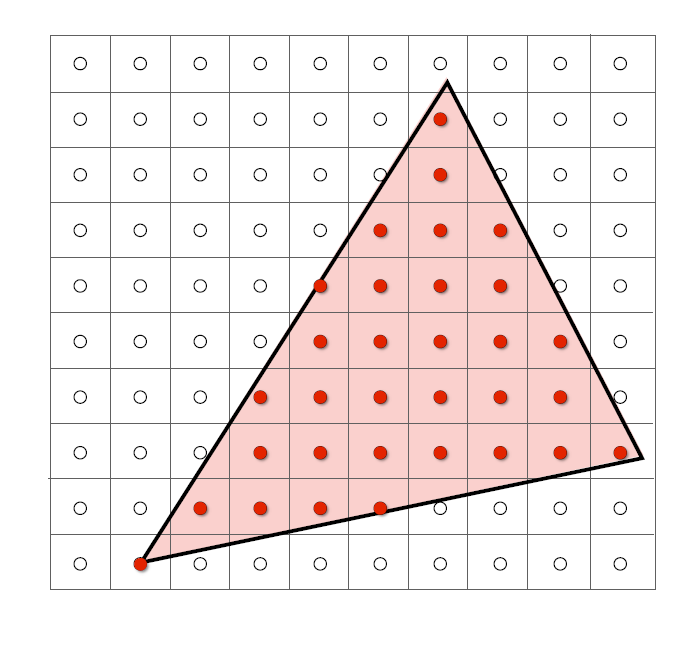
对屏幕中的每一个像素进行采样,如果这个像素点在三角形之中那么这个像素点就应该被采用
判断一个点是否在三角形内,在第二次的时候有讲到过,直接利用顺序叉乘即可
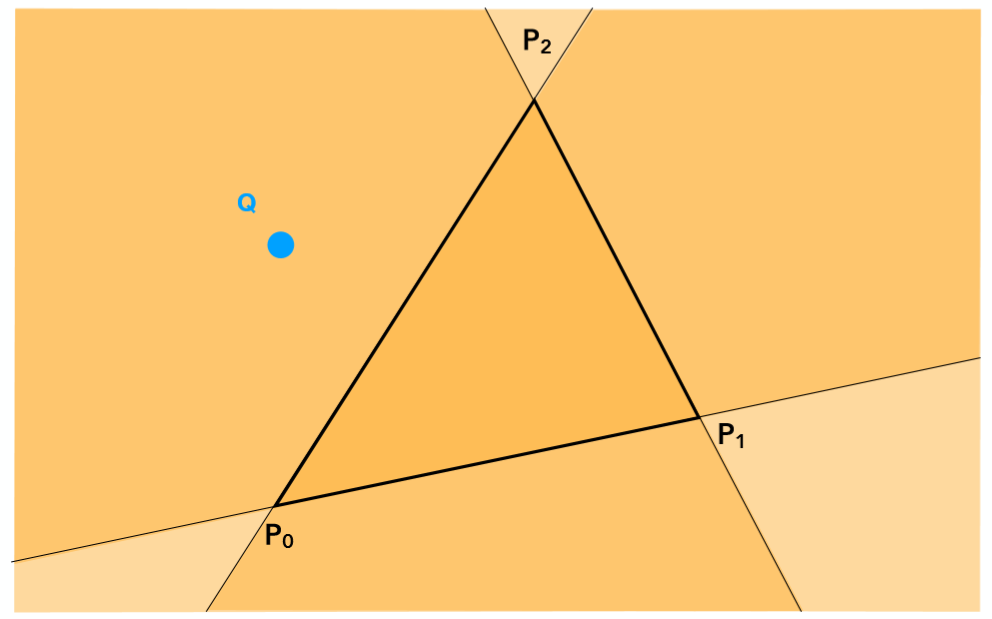
如图所示,我们事先知道想要光栅化的三角形的三个顶点P0,P1,P2,以及检测点Q。分别计算
P
0
P
1
×
P
0
Q
P
1
P
2
×
P
1
Q
P
2
P
0
×
P
2
Q
P_{0} P_{1} \times P_{0} Q \\P_{1} P_{2} \times P_{1}Q \\P_{2} P_{0} \times P_{2} Q
P0P1×P0QP1P2×P1QP2P0×P2Q
如果三者同号则代表点P在三条线段的同一边,那么必然处于三角形内部,如果不同号则代表该点一定在三角形外部!
注意:一定要注意计算的顺序,比如01->12->20,这样才可以!
所以,通过上述算法,只需要遍历每一个点就可以得出三角形的光栅化结果了!当然还可以进一步的进行优化,因为没有必要去测试屏幕中的每一个点,一个三角形面可能只占屏幕很小的部分,可以利用一个bounding box 包围住想要测试的三角形,只对该bounding box内的点进行采样测试
比如:
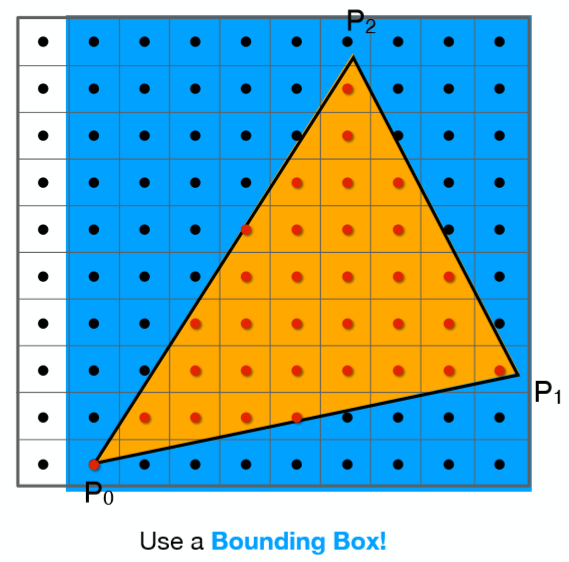
这样就完成了三角形的光栅化
但是还有一点需要去注意:
如果一个点正好处于两个三角形的公共边之上那么,这个点该算作是哪个三角的呢
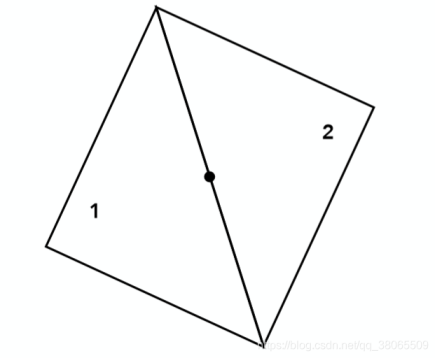
答案是只要你自己规定好就行,无所谓算哪个三角形的!
Antialiasing 反走样
Antialiasing 锯齿走样
比如:

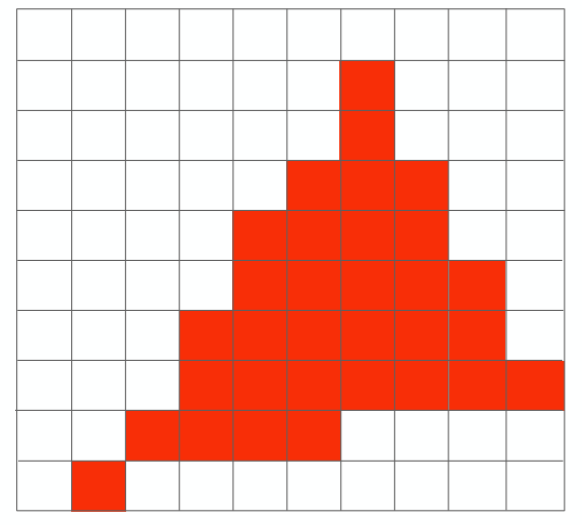
当我们做完光栅化后,会出现上述问题,这种问题本质是因为我们在采样的时候的频率过低无法跟上图像的频率,导致最后结果的失真,也就是说,拟合的并不是很准确
通俗来说,就是:我们用有限离散的像素点去逼近连续的三角形,那么自然会出现这种锯齿走样的现象,因为这种近似是不准确的。
解决措施:
当然,首先可以想到的时增大屏幕的分辨率,想象一下,如果一个像素点可以足够的小,那么,我们就可以无限的离散像素点去逼近真实的图像
但是,这物理设备的问题我们无法去干预,所以,如何在软件的层面上去改进,一个原理是通过把一个实体的一个像素点再多分成多个像素点,然后,将这些一个实体像素点内的多个像素点的表示值进行求平均运算,得到一个平均的表现颜色来表示,效果就会有很大的改善
具体解决方案如下:
Super sampling anti aliasing(SSAA) 超采样反走样
也就是上面提到的:如果有限离散像素点逼近结果不好,那么我们用更多的采样点去逼近不就会得到更好的结果了吗?所以根据这个思想我们可以把原来的每个像素点进行细分,就如下面这个样子:
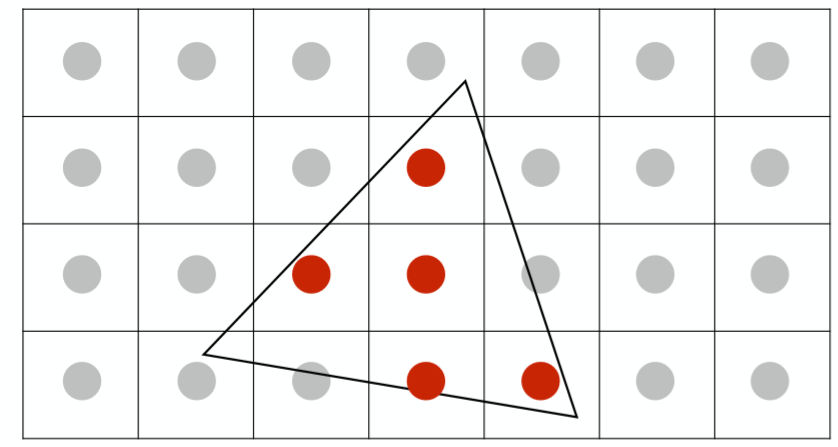
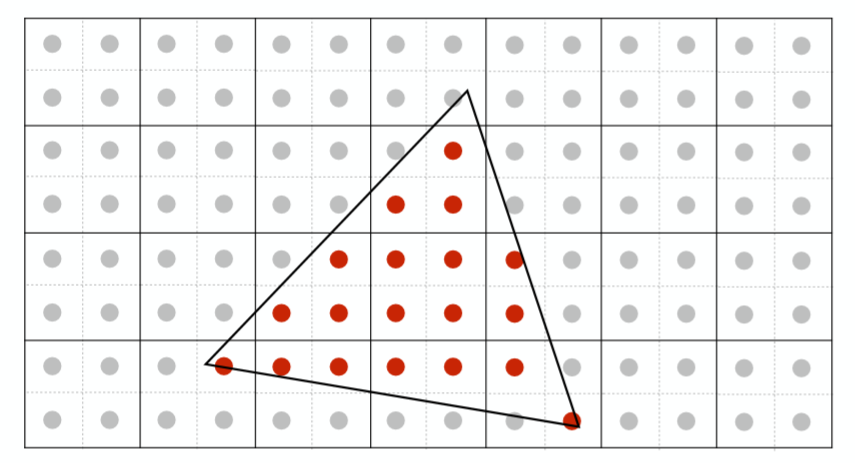
然后,我们根据每个采样点来进行shading(为计算每个像素点的颜色的过程,当然这里是一个纯红色的三角形,如果该点在三角形内,它的颜色值可以直接得到为(1,0,0)),这样得到了每个采样点的颜色之后,我们讲每个像素点内部所细分的采样点的颜色值全部加起来再求均值,作为该像素点的抗走样之后的颜色值!
例如:
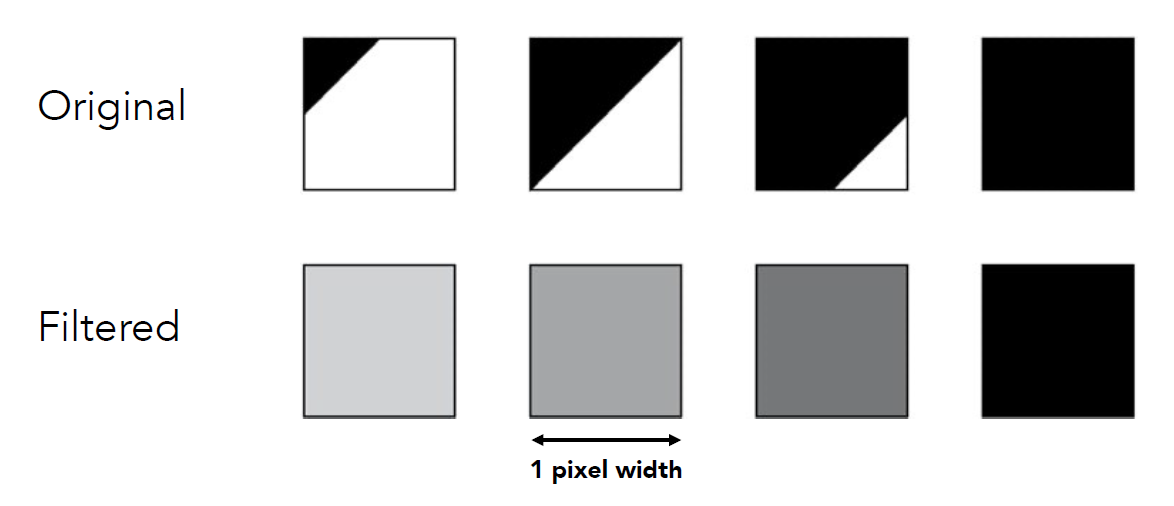
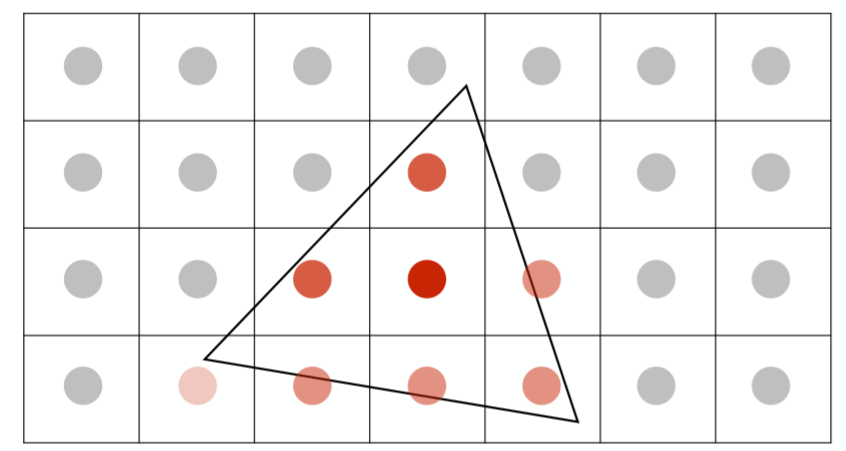
一个利用SSAA抗锯齿更为直观的例子:

Multi-Sampling AA 多采样反走样(MSAA)
MSAA其实是对SSAA的一个改进,如果,每个像素点分成4个采样点,我们就要进行4次的加和再求平均来计算颜色,额外多了4倍的计算量,所以就有了这个改进的算法MSAA
MSAA的做法也很容易理解,我们依然同样会分采样点,但是只会去计算究竟有几个采样点会被三角形cover,计算颜色的时候只会利用像素中心坐标计算一次颜色(即所有的信息都会被插值到像素中心然后取计算颜色),如下图:
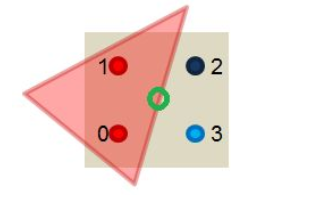
也就是等于:
颜色值 ( R , G , B ) × 被 c o v e r 的 点 数 一 个 像 素 点 内 的 总 的 采 样 点 个 数 \text{颜色值}(R,G,B) \times \frac{被cover的点数}{一个像素点内的总的采样点个数} 颜色值(R,G,B)×一个像素点内的总的采样点个数被cover的点数
再比如:
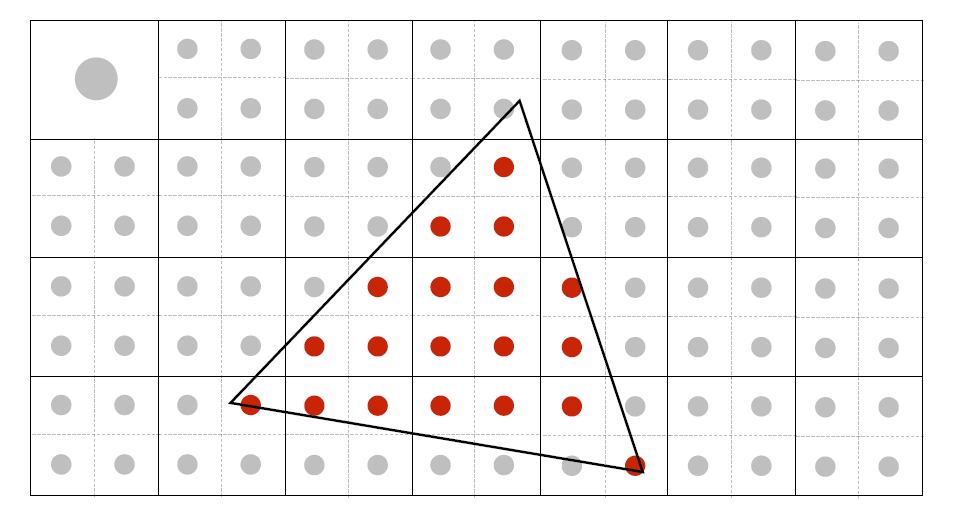
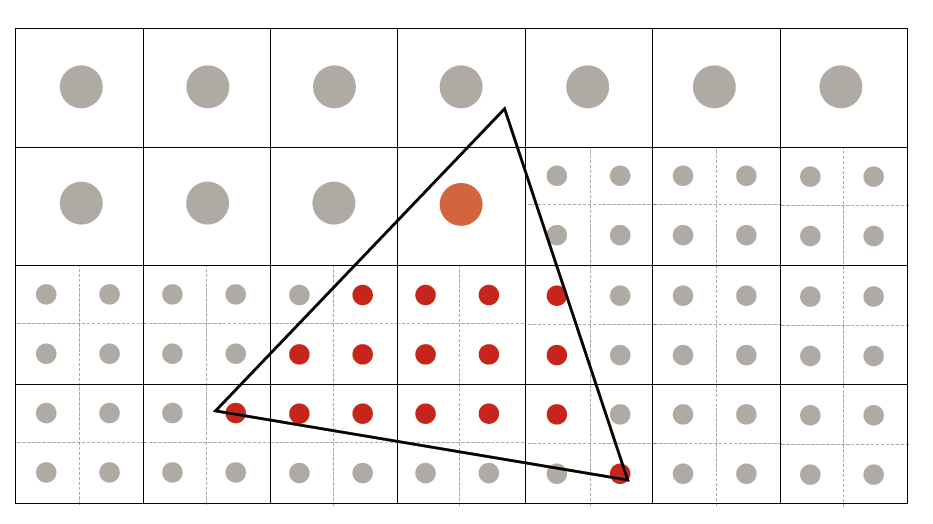
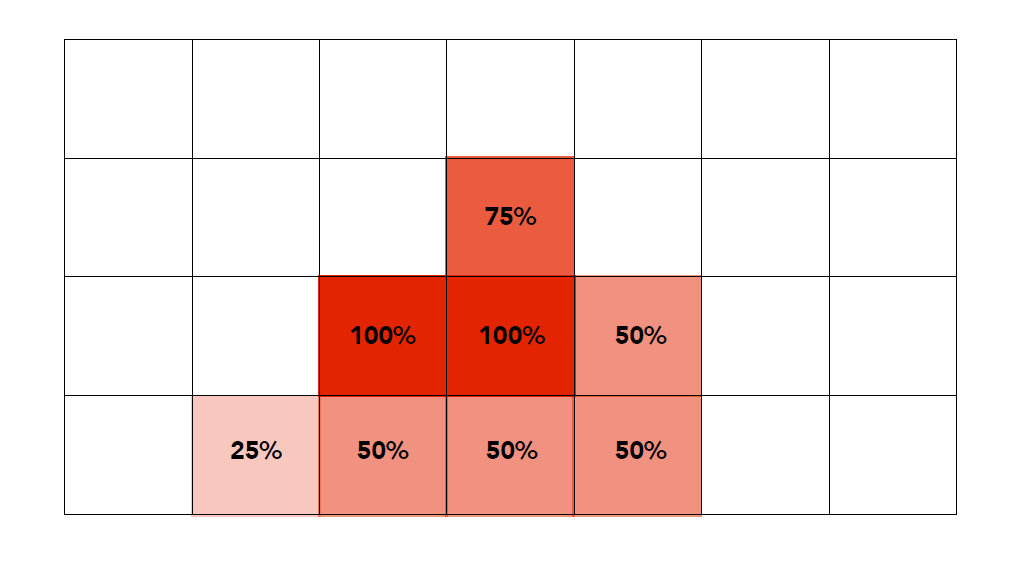
Z-Buffering 算法
解决了走样问题之后,还有一个仍需解决的问题,我们如何判断物体先后关系?
更具体的说每个像素点所对应的可能不止一个三角形面上的点,我们该选择哪个三角形面上的点来显示呢?
答案显然易见,离摄像头最近的像素点显示。
这里便要利用到我们之前做MVP变换之后所得到的深度值Z了,这里定义Z越大离摄像机越远!
Z-Buffering算法:(所有的操作都是针对像素来说的)
本质来说,就是对每个像素都在求最小值,也就是距离摄像机最近的那个点的颜色值
- Z-Buffer算法需要为每个像素点维持一个深度数组记为zbuffer,其每个位置初始值置为无穷大(即离摄像机无穷远)。
- 随后我们遍历每个三角形面上的每一个像素点[x,y]
- 如果该像素点的深度值z,小于
zbuffer[x,y]中的值,则更新zbuffer[x,y]值为该点深度值z,并同时更新该像素点[x,y]的颜色为该三角形面上的该点的颜色
- 如果该像素点的深度值z,小于

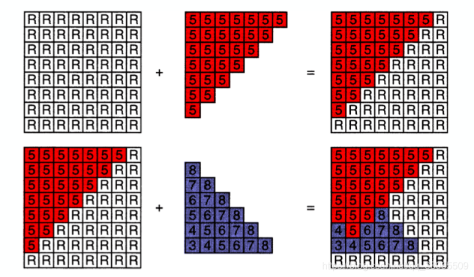
例如:























 274
274

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










