高数第八章_空间解析几何

//仅记录本人认为重要且难以理解记忆的

8.1

方向角

==========>

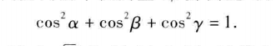
投影
向量a在u上的投影:|a| cosB (B表示a与u的夹角)
或 au/|u|(向量 a点乘向量u再乘上向量u的模)

---

8.2 数量积与向量积

数量积:
定义:a·b=|a| |b| cosB,B表示夹角
也做:|a| Prja b(a的模乘以b在a上的投影)
cosB =a·b/ |a| |b|

向量积
定义向量c与a b垂直且符合右手法则
c=aXb
|c| = |a| |b| sinB ①

以向量a,b为邻边的平行四边形的面积S =|aXb|(也就是①式)
aXa=0(叉乘的结果还是向量)

a,b都是非0向量,aXb=0,则向量a b平行
PS:叉乘不满足交换律
aXb=
向量关系

①a//b<------>aXb=0<------->对应向量比值相等

②a⊥b<----->a·b<------>axbx+ayby+azbz=0;

③abc共面<------>[aXb]·c=0<--------->三个向量所列出的行列式值为0

8.3平面及其方程

平面的点法式方程: A(x-x0)+B(y-y0)+C(z-z0)=0;
法向量:n=(A,B,C); 平面上一点:(x0,y0,z0)

**平面的一般式方程:**Ax+By+Cz+D=0;
其中:平面的法向量为(A,B,C)

特殊情况
A=0 平行或包含x轴
A,B =0 平行xoy面

两平面的夹角
两平面法线的夹角,(通常是锐角或直角)

8.4 空间直线及其方程

一般方程

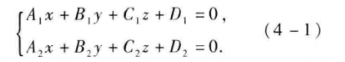
点向式方程
(x-x0)/m=(y-y0)/n=(z-z0)/p
方向向量n=(m,n,p);

参数方程

两直线的夹角
即两直线方向向量的夹角,通常是锐角或直角

直线与平面的夹角
[0,Π/2]
直线与它在平面上的投影形成的夹角
直线与平面的夹角B=| Π-方向向量与法向量的夹角 |
注意是sin,不是cos

8.5曲面及其方程

①旋转曲面
)
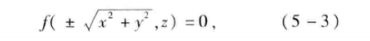绕谁旋转谁不变,平方变成平方和

②柱面
方程中缺一个字母的就是柱面
原因:当绕z轴旋转时,母线平行于z轴
柱面方程:假设绕z轴旋转, X2+Y2=R2;
特殊情况:抛物柱面

③六种二次曲面
一. 椭圆锥面
平面内的椭圆方程为

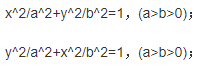
空间内托圆锥面:


二.椭球面
平面内的椭圆

空间内的椭球面
.

五.椭球抛物面

三.单叶双曲面
平面内双曲线方程

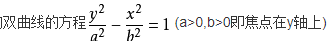
空间内单叶双曲线方程


四.双叶双曲线

六双曲抛物面(马鞍面)

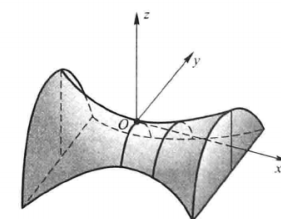
8.6空间曲线在坐标面上的投影曲线

xoz面上的投影曲线

{ 曲线方程消去y得到投影柱面
{
{令y=0,相当于用 yoz面曲截这个投影柱面
两式联立得到了所求投影曲线