多智能体博弈论文学习（3）Task Assignment for Multiplayer Reach-Avoid Games via Analytical Barriers

论文原文：Task Assignment for Multiplayer Reach-Avoid Games in Convex Domains via Analytical Barriers

这篇论文的作者和上一篇阅读笔记的作者是同一人，如果对于barrier是如何解析计算感兴趣可以去上一篇看看：多智能体博弈论文学习（2）Reach-Avoid Games With Two Defenders and One Attacker: An Analytical Approach。

这篇论文相对于上一篇有什么创新？

1. 上一篇仅考虑了2 pursuers VS 1 evader的情况，没有考虑更复杂的协同。
2. 上一篇仅考虑了长方形的区域，并且pursuers初始都位于play region中。

论文的主要贡献

1. 解析计算2 pursuers VS 1 evader情况下的barrier。
2. 解析计算多个pursuers对单个evader的barrier。（首次解析地解决了超过3个player的RA博弈的界栅构造问题）
3. 使用0-1规划求解pursuers到拦截任务的任务分配问题，由于barrier的先验信息，计算量被大大简化。
4. 上述所有方法都是解析的，并且可以实时更新。

一、摘要

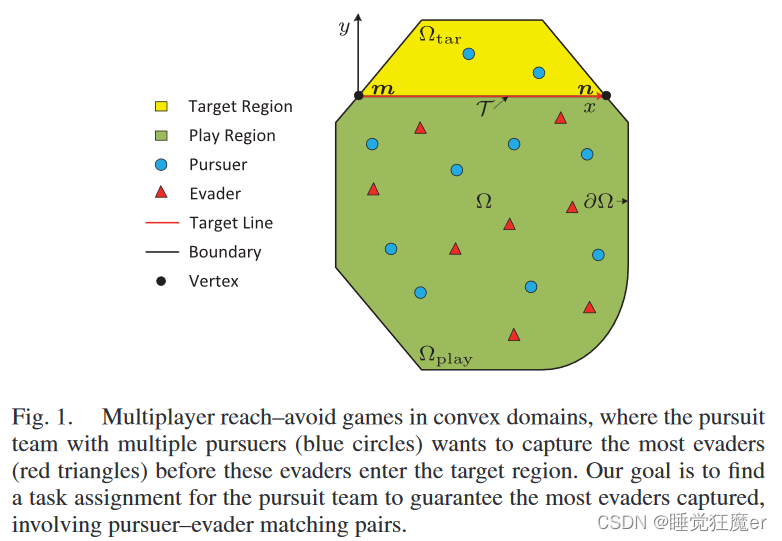
这篇论文考虑一个有界凸区域内的多玩家reach-avoid博弈问题。玩家分为两个敌对的阵营，分别是pursuers和evaders。pursuers的目标是尽可能在evaders到达target region前拦截所有evaders，而evaders的目标是避免被pursuers拦截并且让尽可能多的evaders到达target region。论文给出了界栅（barrier）的解析计算方法，提出了一种使用简化0-1规划方法求解任务分配问题，能够保证最多的evaders被拦截并且避免了求解NP问题。论文提出的所有方法都是解析的。

二、主要内容

2.1 问题陈述

pursuers集合： { P i } i = 1 N p = { P 1 , … , P N p } \{P_{i}\}_{i=1}^{N_{p}}=\{P_{1},\ldots,P_{N_{p}}\} {Pi​}i=1Np​​={P1​,…,PNp​​}。evaders集合： { E j } j = 1 N e = { E 1 , … , E N e } \{E_{j}\}_{j=1}^{N_{e}}=\{E_{1},\ldots,E_{N_{e}}\} {Ej​}j=1Ne​​={E1​,…,ENe​​}。玩家的位置可以用如下的状态方程描述：
$$\begin{array}{rl}{\dot{\mathbf{x}}}_{P_i}(t)& =v_{P_i}{\mathbf{u}}_{P_i}(t),{\mathbf{x}}_{P_i}(0)={\mathbf{x}}_{P_i}^0,i=1,\dots ,N_p\\ {\dot{\mathbf{x}}}_{E_j}(t)& =v_{E_j}{\mathbf{u}}_{E_j}(t),{\mathbf{x}}_{E_j}(0)={\mathbf{x}}_{E_j}^0,j=1,\dots ,N_e\end{array}\text{\hspace{1em}(1)}$$
其中控制量$\mathbf{u}$是一个模为1的二维向量，所有的pursuers是同构的，即最大速度$v_P$是相等的，所有的evaders是同构的，即最大速度$v_E$是相等的。

游戏双方胜利条件与多智能体博弈论文学习（2）Reach-Avoid Games With Two Defenders and One Attacker: An Analytical Approach相同，play region、target region等等定义也类似，本文不再赘述，感兴趣的读者可以自行查阅。

pursuers之间可以结为联盟（coalition），联盟包含的pursuers数量可能是1，2，……，$N_p$，那么所有可能的联盟数共有$2^{N_p-1}$个，每个联盟可以用如下的定义表示

定义1（Binary Coalition for Pursuit Team）：$k$的第$i$位二进制数为1则$P_i$属于联盟$k$。联盟$k$中包含的所有pursuers的序号用集合 I k = { m j ∣ 1 ≤ m j ≤ N p , j = 1 , 2 , … , n k } \mathcal{I}_{k}=\{m_{j}|1\leq m_{j}\leq N_{p},j=1,2,\ldots,n_{k}\} Ik​={mj​∣1≤mj​≤Np​,j=1,2,…,nk​}表示，其中$n_k$是联盟$k$包含的pursuers数量。（例如联盟5的二进制表示为“101”， I 5 = { P 1 , P 3 } \mathcal{I}_{5} = \{P_1, P_3\} I5​={P1​,P3​}。

定义2（Pursuit Subcoalition）：如果联盟$k_1$的所有pursuers都在$k_2$中，那么联盟$k_1$称为$k_2$的subcoalition。

为什么所有可能的联盟数共有$2^{N_p-1}$个？
想象把所有pursuers排成一列，如果要将它分成$m$份，那么只需要从中间抽出$m-1$个即可，那么总共就有
$$\sum _{m=1}^{N_p}{C}_{N_p}^m=\sum _{m=0}^{N_p}{C}_{N_p}^m-C_{N_p}^0=2^{N_p-1}$$

假设1（Isolate Initial Deployment）：每个Player初始的位置都不同。

假设2（Constrained Initial Deployment）：pursuers初始位置满足${\mathbf{x}}_{P_i}^0\in {\Omega }_{\mathrm{play}}\cup \mathcal{T}$，evaders初始位置满足${\mathbf{x}}_{E_j}^0\in {\Omega }_{\mathrm{play}}$

假设3（Relaxed Initial Deployment）：pursuers初始位置满足${\mathbf{x}}_{P_i}^0\in \Omega$，evaders初始位置满足${\mathbf{x}}_{E_j}^0\in {\Omega }_{\mathrm{play}}$

假设4（Speed Ratio）：定义$\alpha =v_E/v_P$，$0<\alpha <1$。

2.2 Preliminaries

2.2.1 ER和BER的计算

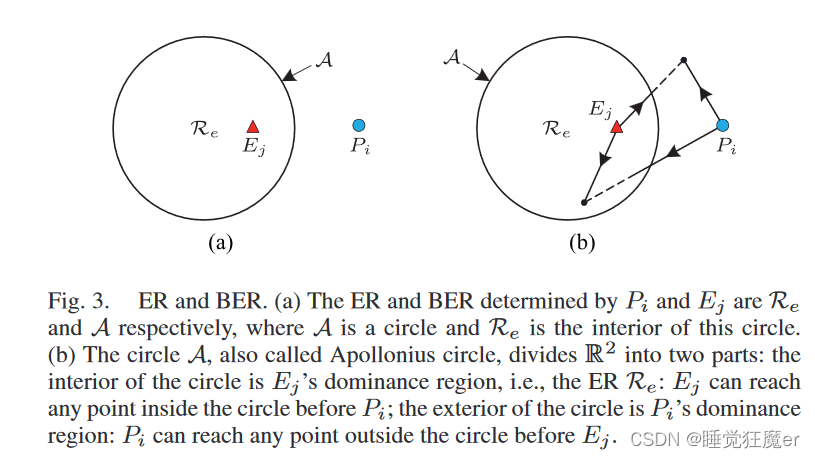
此处的计算类似Apollonius Circle，ER（evasion region）是Evader能够比Pursuer更快到达的区域，ER的边界称为BER（Boundary of ER）。按照定义，ER和BER可以分别表示为：
$$\begin{array}{rl}{\mathcal{R}}_e& =\left\{\mathrm{z}\in {\mathbb{R}}^2|\Vert \mathrm{z}-{\mathrm{x}}_{E_j}^0{\Vert }_2<\alpha \Vert \mathrm{z}-{\mathrm{x}}_{P_i}^0{\Vert }_2\right\}\\ \mathcal{A}& =\left\{\mathrm{z}\in {\mathbb{R}}^2|\Vert \mathrm{z}-{\mathrm{x}}_{E_j}^0{\Vert }_2=\alpha \Vert \mathrm{z}-{\mathrm{x}}_{P_i}^0{\Vert }_2\right\}\end{array}$$
对于${\mathcal{R}}_e$的不等式进行变形，可以得到：
$$\begin{array}{rl}& \Vert \mathbf{z}-{\mathbf{x}}_{E_j}^0{\Vert }_2^2<{\alpha }^2\Vert \mathbf{z}-{\mathbf{x}}_{P_i}^0{\Vert }_2^2\\ & \Rightarrow \Vert \mathrm{z}{\Vert }_2^2-2\frac{{\left({\mathbf{x}}_{E_j}^0-{\alpha }^2{\mathbf{x}}_{P_i}^0\right)}^{\mathsf{T}}\mathbf{z}}{1-{\alpha }^2}<\frac{{\alpha }^2\Vert {\mathbf{x}}_{P_i}^0{\Vert }_2^2-\Vert {\mathbf{x}}_{E_j}^0{\Vert }_2^2}{1-{\alpha }^2}\\ & \Rightarrow {\Vert \mathbf{z}-\frac{{\mathbf{x}}_{E_j}^0-{\alpha }^2{\mathbf{x}}_{P_i}^0}{1-{\alpha }^2}\Vert }_2^2<\frac{{\alpha }^2\Vert {\mathbf{x}}_{E_j}^0-{\mathbf{x}}_{P_i}^0{\Vert }_2^2}{(1-{\alpha }^2{)}^2}\\ & \Rightarrow {\Vert \mathbf{z}-\eta \left({\mathbf{x}}_{E_j}^0,{\mathbf{x}}_{P_i}^0\right)\Vert }_2^2<r^2\left({\mathbf{x}}_{E_j}^0,{\mathbf{x}}_{P_i}^0\right)\end{array}$$

其中$\eta$和$r$的定义如下：
$$\begin{array}{rl}r(\mathbf{x},\mathbf{y})& =\frac{\alpha \Vert \mathbf{x}-\mathbf{y}{\Vert }_2}{1-{\alpha }^2}\\ \eta (\mathbf{x},\mathbf{y})& =\frac{\mathbf{x}-{\alpha }^2\mathbf{y}}{1-{\alpha }^2}\end{array}$$

2.2.2 Key Function

引理1（Monotony of Function）：设BER与$y=0$的交集 A ∩ { z ∈ R 2 ∣ y = 0 } = { ( c 1 , 0 ) , ( c 2 , 0 ) } \mathcal{A}\cap \{\mathbf{z}\in\mathbb{R}^2|y=0\}=\big\{(c_1,0),(c_2,0)\big\} A∩{z∈R2∣y=0}={(c1​,0),(c2​,0)}，且$c_1<c_2$，$x_{P_i}^0\le x_{E_j}^0$，则函数
$$G_1(x_p)={\Vert \mathbf{p}-{\mathbf{x}}_{P_i}^0\Vert }_2-\frac{{\Vert \mathbf{p}-{\mathbf{x}}_{E_j}^0\Vert }_2}{\alpha },\mathbf{p}=(x_p,0)$$
在区间$x_p\in [c_1,x_p^{\ast }]$严格单调递增，在区间$x_p\in [x_p^{\ast },c_2]$严格单调递减。其中，$x_p\in [c_1,c_2]$可以由如下的方程求解
$$\frac{x_p^{\ast }-x_{P_i}^0}{{\Vert p^{\ast }-{\mathrm{x}}_{P_i}^0\Vert }_2}=\frac{x_p^{\ast }-x_{E_j}^0}{\alpha {\Vert p^{\ast }-{\mathrm{x}}_{E_j}^0\Vert }_2},p^{\ast }=(x_p^{\ast },0)$$

证明过程与上一篇论文阅读笔记类似

2.3 One Pursuit Coalition VS One Evader

这一节讨论了一个Pursuit Coalition VS One Evader的情形，记 X k 0 = { x P m 1 0 , … , x P m n k 0 } ∈ R 2 n k \mathcal{X}_{k}^{0}=\{\mathrm{x}_{P_{m_{1}}}^{0},\ldots,\mathrm{x}_{P_{mn_{k}}}^{0}\}\in\mathbb{R}^{2n_{k}} Xk0​={xPm1​​0​,…,xPmnk​​0​}∈R2nk​和 P k = { u P m 1 , … , u P m n k } ∈ U n k \mathcal{P}_k=\{\mathbf{u}_{P_{m_1}},\ldots,\mathbf{u}_{P_{m_{n_k}}}\}\in\mathcal{U}^{n_k} Pk​={uPm1​​​,…,uPmnk​​​​}∈Unk​是pursuit coalition $k$的初始位置集和控制量集合。需要解决两个问题：

1. 如果evader初始位于pursuit winning region，求出pursuers的控制量集合以拦截evader
2. 如果evader初始位于evasion winning region，求出evader的控制量以到达target region
   要解决这个问题，首先需要求解出PWR和EWR以及他们的分界线Barrier，如下图的${\mathcal{W}}_E^1$、${\mathcal{W}}_P^1$和${\mathcal{B}}^1$。
   

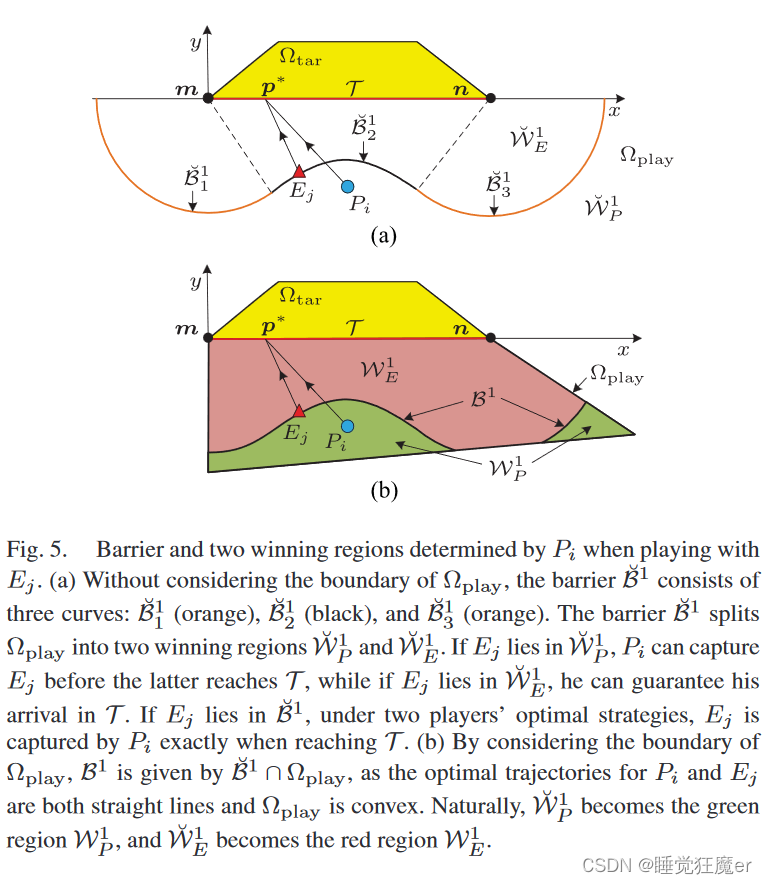
根据pursuer是否影响Barrier的形状、位置，论文给出了如下的定义

定义3（Active and Inactive Pursuers）：对于pursuer $P_i(i\in {\mathcal{I}}_k)$，如果在target line $\mathcal{T}$上存在一点使得$P_i$能够比$k$中其他pursuers更快到达，那么就称$P_i$是一个active pursuer，否则称为inactive pursuer。

active和inactive是相对的，一个pursuer是否是active的取决于evader的位置以及联盟中其他pursuers的位置。也就是说，在联盟$k$中一个active的pursuer可能在另一个联盟中是inactive的，反之同理。

为了求解玩家的最优策略，论文定义了如下的收益函数：
定义4（Payoff Function）：对于联盟$k$和逃避者$E_j$，如果$E_j$能够成功到达$\mathcal{T}$，则将$E_j$到达KaTeX parse error: Undefined control sequence: \matchal at position 1: \̲m̲a̲t̲c̲h̲a̲l̲ ̲T时到其最近的pursuer的距离记为收益函数$J$，$J$和它对应的价值函数$V$分别具有如下形式
$$J=\underset{i\in {\mathcal{I}}_k}{\min }\Vert {\mathbf{x}}_{P_i}(t_1)-{\mathbf{x}}_{E_j}(t_1){\Vert }_2,V=\underset{{\mathcal{P}}_k\in {\mathcal{U}}^{n}k}{\min }\underset{{\mathbf{u}}_{E_j}\in \mathcal{U}}{\max }J$$
其中$t_1$是$E_j$首次到达$\mathcal{T}$的时刻。

根据这个收益函数，可以使用Reach-Avoid Games With Two Defenders and One Attacker: An Analytical Approach中的方法计算Barrier和optimal target，与之前的方法类似，利用一阶必要条件计算fixed optimal target和unfixed optimal target，然后计算对应的Barrier，本文不再赘述，感兴趣的读者可以自行查阅这两篇论文。

2.4 General Pursuit Coalitions VS One Evader

这一部分中，论文将2 Pursuers VS 1 Evader的情况进行了推广，主要有以下几点：

1. 研究了联盟中所有pursuers均为active pursuer的情况
2. 说明了每一个一般的联盟都可以唯一退化为所有成员均为active pursuers的子联盟
3. 证明了退化后的子联盟与原联盟拥有相同的barrier
4. 给出了这种特殊的联盟的定义

定义6（Full-Active Pursuit Coalition）：给定联盟 $k$，如果对于任何$P_i\left(i\in {\mathcal{I}}_k\right)$，总是存在$\mathcal{T}$上一点使得$P_i$能够比$k$中其他pursuers更快到达，那么$k$称为full-active pursuit coalition。

Full-active pursuit coalition的barrier求解过程与one coalition VS one Evader类似，结果如下图所示

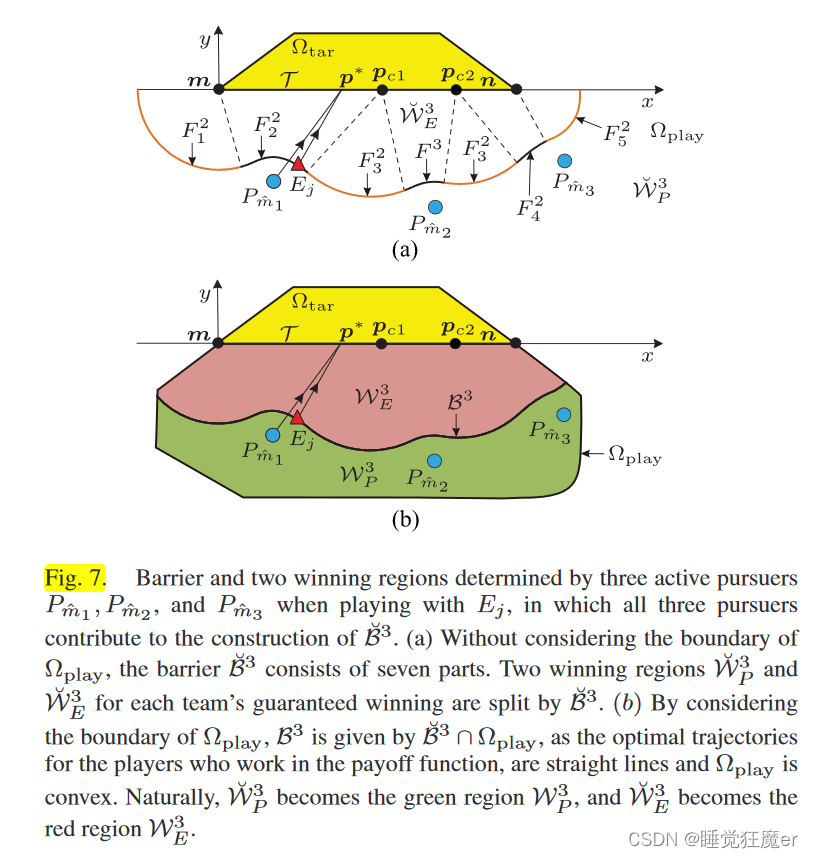
一般的联盟中存在部分inactive pursuers，这些pursuers会增加分析的复杂程度，为了直接使用full-active pursuit coalition的结论，论文提出了一种方法来从一般的联盟中提取最大的full-active pursuit coalition。

引理3（Barrier Equivalence）：对于任意的联盟$k$，${\mathcal{B}}^{n_k}({\mathcal{X}}_k^0)={\mathcal{B}}^{{\bar{n}}_k}({\bar{\mathcal{X}}}_k^0)$成立，其中${\bar{\mathcal{X}}}_k^0$是${\mathcal{X}}_k^0$的largest full-active pursuit coalition，其中包含${\bar{n}}_k$个pursuers。

Lemma 3的证明
显然，当${\mathcal{X}}_k^0\setminus {\bar{\mathcal{X}}}_k^0$为空集，即原coalition与largest full-active pursuit coalition相同时，Lemma 3成立。对于$n_k>{\bar{n}}_k$的情况，只需证明${\mathcal{W}}_E^{n_k}={\mathcal{W}}_E^{{\bar{n}}_k}$即可。

根据定义，如果从${\mathcal{X}}_k^0$中去掉几个pursuer，则${\mathcal{W}}_E^{n_k}$一定会扩大（去掉active pursuer）或者不变（去掉inactive pursuer），所以我们可以得到${\mathcal{W}}_E^{n_k}\subseteq {\mathcal{W}}_E^{{\bar{n}}_k}$，因此只需证明${\mathcal{W}}_E^{{\bar{n}}_k}\subseteq {\mathcal{W}}_E^{n_k}$即可，等价的，只需证明${\check{\mathcal{W}}}_E^{{\bar{n}}_k}\subseteq {\check{\mathcal{W}}}_E^{n_k}$。

设$\mathbf{p}\in {\check{\mathcal{W}}}_E^{{\bar{n}}_k}$，则必存在${\mathbf{p}}_1\in \mathcal{T}$使对于所有的${\mathbf{x}}_{P_i}^0\in {\bar{\mathcal{X}}}_k^0$都有
$$\Vert \mathbf{p}-{\mathbf{p}}_1{\Vert }_2<\alpha \Vert {\mathbf{x}}_{P_i}^0-{\mathbf{p}}_1{\Vert }_2\text{\hspace{1em}(43)}$$

假设${\mathbf{x}}_{P_j}^0\in {\mathcal{X}}_k^0\setminus {\bar{\mathcal{X}}}_k^0$，并且满足
$$\alpha {\Vert \begin{array}{c}{\mathbf{x}}_{P_j}^0-{\mathbf{p}}_1\end{array}\Vert }_2\le {\Vert \begin{array}{c}\mathbf{p}-{\mathbf{p}}_1\end{array}\Vert }_2\text{\hspace{1em}(44)}$$

联立上述两个不等式有
$${\Vert {\mathbf{x}}_{P_j}^0-{\mathbf{p}}_1\Vert }_2<{\Vert {\mathbf{x}}_{P_i}^0-{\mathbf{p}}_1\Vert }_2\text{\hspace{1em}(45)}$$
说明${\mathbf{x}}_{P_j}^0$能够比其他pursuers更快到达${\mathbf{p}}_1$，与${\bar{\mathcal{X}}}_k^0$是largest full-active pursuit subcoalition矛盾，因此式(44)不成立，即对于所有的${\mathbf{x}}_{P_j}^0\in {\mathcal{X}}_k^0\setminus \overline{{\mathcal{X}}_k^0}$都有
$$\Vert \mathbf{p}-{\mathbf{p}}_1{\Vert }_2<\alpha \Vert {\mathbf{x}}_{P_j}^0-{\mathbf{p}}_1{\Vert }_2\text{\hspace{1em}(46)}$$
由(43)到(46)我们可以得到如下结论

存在${\mathbf{p}}_1\in \mathcal{T}$使得$\mathbf{p}$能够比${\mathcal{X}}_k^0$中的所有pursuers更快到达，因此，$\mathbf{p}\in {\check{\mathcal{W}}}_E^{n_k}$，说明${\breve{W}}_E^{{\bar{n}}_k}\subseteq {\breve{W}}_E^{n_k}$，证毕。

Largest full-active pursuit subcoalition存在性与唯一性的说明

${\bar{\mathcal{X}}}_k^0\subseteq {\mathcal{X}}_k^0$，因此存在性显然成立。

假设${\bar{\mathcal{X}}}_k^0$和${\bar{\mathcal{Y}}}_k^0$是分别具有${\bar{n}}_k$和${\bar{m}}_k$的两个largest full-active pursuit subcoalition，从中选取一个${\mathbf{x}}_{P_i}^0\in \overline{{\mathcal{X}}_k^0}$且${\mathbf{x}}_{P_i}^0\notin {\bar{\mathcal{Y}}}_k^0$，则$P_i$不可能比${\bar{\mathcal{Y}}}_k^0$中的pursuers更早到达$\mathcal{T}$，这与${\bar{\mathcal{X}}}_k^0$中的pursuers均为active矛盾，唯一性得证。

记${\mathcal{R}}_D$是$P_{m_i}$能够比$P_{m_j}$更早到达的点的集合，即
$$\begin{array}{rl}{\mathcal{R}}_D({\mathbf{x}}_{P_{m_i}}^0,{\mathbf{x}}_{P_{m_j}}^0)& =\{\mathbf{z}\in {\mathbb{R}}^2|\Vert \mathbf{z}-{\mathbf{x}}_{P_{m_i}}^0{\Vert }_2<\Vert \mathbf{z}-{\mathbf{x}}_{P_{m_j}}^0{\Vert }_2\}\end{array}$$

基于上述分析，论文给出了寻找一个pursuit coalition的largest full-active pursuit coalition的算法：

定理4（Barrier for General Pursuit Coalition）：考虑满足假设1、2、4的系统（1），对于pursuit coalition $k$ ，它的largest full-active pursuit subcoalition ${\bar{\mathcal{X}}}_k^0$（包含${\bar{n}}_k$个pursuers）可以通过算法1被找到，它的barrier可以通过定理3计算。

2.5 Extensions to Relaxed Initial Deployment

之前的分析都是基于假设3的，这就要求pursuers初始位置位于play region中，在这一部分中，论文对通过引入Virtual Pursuer的概念，将barrier和winning region的计算推广到了初始位置可以位于target region的情况。

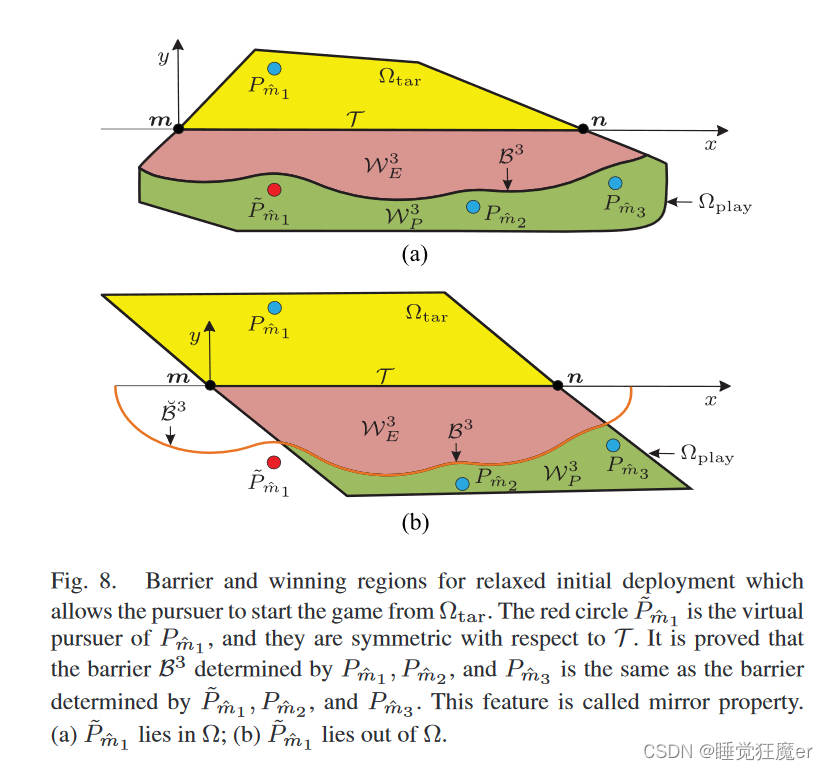
定义7（Virtual Pursuer）：对于每个满足${\mathbf{x}}_{P_i}^0=(x_{P_i}^0,y_{P_i}^0)\in {\Omega }_{\mathrm{tar}}$的pursuer $P_i$，引入一个virtual pursuer ${\tilde{P}}_i$，满足${\tilde{\mathbf{x}}}_{P_i}^0=({\tilde{x}}_{P_i}^0,{\tilde{y}}_{P_i}^0)$且${\tilde{x}}_{P_i}^0=x_{P_i}^0$，${\tilde{y}}_{P_i}^0=-y_{P_i}^0$

由于virtual pursuer可能导致假设1不成立，因此将假设1修改为如下的假设5：

假设5：假设每个virtual pursuer都不与其他pursuers重合，但是允许virtual pursuer与其origin pursuer重合，即${\mathbf{x}}_{P_i}^0\in \mathcal{T}$

引理4（Mirror Property）：对于$k$，若${\mathbf{x}}_{P_i}^0\in {\Omega }_{\text{tar }}(i\in {\mathcal{I}}_k)$，令${\mathcal{X}}_k^0(-i)$表示去掉${\mathbf{x}}_{P_i}$后的其他pursuers的初始位置集合，${\tilde{\mathbf{x}}}_{P_i}^0$表示${\mathbf{x}}_{P_i}$的virtual pursuer，则有如下结论成立
$${\mathcal{B}}^{n_k}({\mathcal{X}}_k^0)={\mathcal{B}}^{n_k}({\mathcal{X}}_k^0(-i)\cup {\tilde{\mathbf{x}}}_{P_i}^0)$$

引理4的证明：设$p\in {\mathcal{W}}_E^{n_k}({\mathcal{X}}_k^0(-i)\cup {\tilde{\mathbf{x}}}_{P_i}^0)$，存在一点${\mathbf{p}}_1\in \mathcal{T}$使得式（48）对于所有的${\mathbf{x}}_{P_j}^0\in {\mathcal{X}}_k^0(-i)\cup {\tilde{\mathbf{x}}}_{P_i}^0$都成立
$$\Vert \mathbf{p}-{\mathbf{p}}_1{\Vert }_2<\alpha \Vert {\mathbf{x}}_{P_j}^0-{\mathbf{p}}_1{\Vert }_2\text{\hspace{1em}(48)}$$

根据定义7，有式（49）成立
$${\Vert {\mathbf{x}}_{P_i}^0-{\mathbf{p}}_1\Vert }_2={\Vert {\tilde{\mathbf{x}}}_{P_i}^0-{\mathbf{p}}_1\Vert }_2\text{\hspace{1em}(49)}$$

因为（48）对所有的${\mathbf{x}}_{P_j}^0\in {\mathcal{X}}_k^0$成立，因此$\mathbf{p}\in {\mathcal{W}}_E^{n_k}({\mathcal{X}}_k^0)$。因此${\mathcal{W}}_E^{n_k}({\mathcal{X}}_k^0(-i)\cup {\tilde{\mathbf{x}}}_{P_i}^0)\subseteq {\mathcal{W}}_E^{n_k}({\mathcal{X}}_k^0)$

另一个方向的包含关系也可以通过类似的方法证明，本处不再赘述。

通过这一引理，论文给出了如下的针对relaxed initial deployment的barrier计算方法。

推论1（Barrier for Relaxed Initial Deployment）：考虑满足假设1，3，4的系统（1），对于一个pursuit coalition $k$，令${\mathcal{X}}_{k,1}^0$和${\mathcal{X}}_{k,2}^0$分别表示初始位置在${\Omega }_{\text{play}}$和${\Omega }_{\text{tar}}$的pursuers，${\mathcal{X}}_{k,2}^0$对应的virtual pursuers的集合为${\tilde{\mathcal{X}}}_{k,2}^0$。则有如下结论成立：
$${\mathcal{B}}^{n_k}({\mathcal{X}}_k^0)={\mathcal{B}}^{n_k}({\mathcal{X}}_{k,1}^0\cup {\tilde{\mathcal{X}}}_{k,2}^0)$$
其中${\mathcal{B}}^{n_k}({\mathcal{X}}_{k,1}^0\cup {\tilde{\mathcal{X}}}_{k,2}^0)$可以通过定理4计算。

2.6 Pursuit Task Assignment

为了找到最优的任务分配来最大化抓捕到的evaders的数量，我们可以利用前面章节的算法首先计算barrier和pursuit winning region，然后通过检查evader初始位置是否位于${\mathcal{W}}_P^{n_k}$来检查其是否可以被某个pursuit coalition抓捕。

记$G=(P,E,\mathcal{E})$为一个二分图，由两个相互独立的节点集合$P$，$E$，以及无向的边集$\mathcal{E}$。若pursuit coalition $i$ 能够确保在 ${\Omega }_{\text{play}}$或者$\mathcal{T}$ 抓捕evader $E_j$，则$e_{ij}\in \mathcal{E}$，否则$e_{ij}\notin \mathcal{E}$。因此，通过计算每个pursuit coalition的barrier，就可以计算出$\mathcal{E}$中的所有边。

如果$\mathcal{E}$的一个子集$M$中的任意两条边都不连接在同一个节点上，则$M$称为一个matching。为了抓捕最多的evader，对应的matching就需要包含最多的边数。需要注意的是，在最后的分配结果中，同一个pursuer不能同时出现在两个pursuit coalition中。为了解决这个问题，可以使用0-1整数规划求解。

引理5（Degeneration of Pursuit Coalition）：对于任意包含$n_k\ge 3$的pursuit coalition $k$，如果存在一个evader $E_j$使得${\mathbf{x}}_{E_j}^0\in {\mathcal{W}}_P^{n_k}$，则必然存在一个$k$的一个pursuit subcoalition $k_1$满足$n_{k_1}=2$且${\mathbf{x}}_{E_j}^0\in {\mathcal{W}}_P^{n_{k_1}}$。

1. 引理5的证明可以通过定理3简单理解，定理三说明了barrier的每个部分最多只与两个pursuers的初始位置有关。
2. 引理5说明，任意最大化evaders抓捕数量的matching都可以被简化为每个pursuit coalition最多包含两个pursuers的情况，因此只需再这样的pursuit coalition中找到一个最优的matching就能保证最多的evaders被抓捕。

由以上引理，下面只需要关注最多包含两个pursuers的pursuit coalition即可，论文将它称为Execution Pursuit Coalition，并且给出了如下的定义：

定义8（Execution Pursuit Coalition）：如果pursuit coalition $k$ 包含的pursuers数$n_k$满足$n_k=1$或者$n_k=2$，则$k$称为一个execution pursuit coalition。

按照定义8，我们不难计算出，包含单个pursuer的coalition有$N_p$个，包含两个pursuers的coalition有$N_p(N_p-1)/2$，那么可能的分配结果共有$N_v=N_e(N_p+N_p(N_p-1)/2)$。进一步我们定义如下的数据结构来记录通过前述章节计算出的先验信息。

定义9（Prior Information Vector）：对于$P_i$，定义${\mathbf{r}}_i=[r_i^1(1),\cdots ,r_i^1(N_e)]\in {\mathbb{R}}^{N_e}$，其中$j=1,\cdots ,N_e$。若${\mathbf{x}}_{E_j}^0\in {\mathcal{W}}_E^1({\mathbf{x}}_{P_i}^0)$，则$r_i^1(j)=0$，即$P_i$不能保证在$E_j$到达$\mathcal{T}$之前抓捕它；反之，则$r_i^1(j)=1$。类似地，定义${\mathbf{r}}_{i1,i2}^2(j)=[r_{i1,i2}^2(1),\cdots ,r_{i1,i2}^2(N_e)]\in {\mathbb{R}}^{N_e}$，若${\mathbf{x}}_{E_j}^0\in {\mathcal{W}}_E^2({\mathbf{x}}_{P_{i1}}^0\cup {\mathbf{x}}_{P_{i2}}^0)$，则$r_{i1,i2}^2(j)=0$；反之，则$r_{i1,i2}^2(j)=1$。定义$\mathbf{r}=[{\mathbf{r}}_1^1,\cdots ,{\mathbf{r}}_{N_p}^1,{\mathbf{r}}_{1,2}^2,\cdots ,{\mathbf{r}}_{1,N_p}^2,\cdots ,r_{2,3}^2,\cdots ,{\mathbf{r}}_{N_p-1,N_p}^2]\in {\mathbb{R}}^{N_v}$为prior information vector。

记${\mathbf{s}}_i^1=[s_i^1(1),\cdots ,x_i^1(N_e)]\in {\mathbb{R}}^{N_e}$为$P_i$的策略向量，$s_i^j=1$表示分配$P_i$去拦截$E_j$，否则$s_i^j=0$。记${\mathbf{s}}_{i_1,i_2}^2=[s_{i_1,i_2}^2(1),\cdots ,s_{i_1,i_2}^2(N_e)]\in {\mathbb{R}}^{N_e}$为pursuit对 { P i 1 , P i 2 } \{P_{i1}, P_{i2}\} {Pi1​,Pi2​}的策略向量，$s_{i_1,i_2}^2(j)=1$表示 { P i 1 , P i 2 } \{P_{i1}, P_{i2}\} {Pi1​,Pi2​}被分配到$E_j$，否则$s_{i_1,i_2}^2(j)=0$。为了确保同一pursuer不会被分配到两个evaders，有如下的不等式

$$\begin{array}{rl}& \sum _{j=1}^{N_e}{s}_i^1(j)\le 1\\ & \sum _{j=1}^{N_e}{s}_{i_1,i_2}^2(j)\le 1\end{array}$$

记所有execution pursuit coalitions的策略向量为$\mathbf{z}=[{\mathbf{s}}^1,{\mathbf{s}}^2{]}^T\in {\mathbb{R}}^{N_v\times 1}$，其中${\mathbf{s}}^1=[{\mathbf{s}}_1^1,\cdots ,{\mathbf{s}}_{N_p}^1]\in {\mathbb{R}}^{N_p{N}_e}$，${\mathbf{s}}^2=[{\mathbf{s}}_{1,2}^2,\cdots ,{\mathbf{s}}_{1,N_p}^2,{\mathbf{s}}_{2,3}^2,\cdots ,{\mathbf{s}}_{N_p-1,N_p}^2]\in {\mathbb{R}}^{N_e{N}_p(N_p-1)/2}$。通过如下的定理5，可以求解出maximum matching。

定理5（Maximum Matching）：考虑满足假设1，3，4的系统（1），给定${\mathcal{X}}_p^0$和${\mathcal{X}}_E^0$，pursuit team能够抓捕的最多的evaders数量$q$可以由如下优化问题求解：
q = max ⁡ c T z s.t.  A 1 z ≤ b 1 A 2 z ≤ b 2 A 3 z ≤ b 3 z = [ s 1 , s 2 ] T = [ z ( 1 ) , ⋯   , z ( N v ) ] T z ( i ) ∈ { 0 , 1 } (50) \begin{aligned} q &= \max \bold c^T \bold z \\ \text{s.t.}\ &A_1\bold z\leq \bold b_1\\ &A_2\bold z \leq \bold b_2 \\ &A_3\bold z\leq \bold b_3 \\ &\bold z = [\bold s^1, \bold s^2]^T = [z(1),\cdots, z(N_v)]^T\\ &z(i)\in\{0,1\} \end{aligned} \tag{50} qs.t. ​=maxcTzA1​z≤b1​A2​z≤b2​A3​z≤b3​z=[s1,s2]T=[z(1),⋯,z(Nv​)]Tz(i)∈{0,1}​(50)
其中，$\mathbf{c}=\text{ones}(N_v,1)$，${\mathbf{b}}_1={\mathbf{r}}^T$，$A_1=I_{N_v}$，${\mathbf{b}}_2=\text{ones}(N_e,1)$，$A_2=\text{ones}(1,N_v/N_e)\otimes I_{N_e}$，${\mathbf{b}}_3=\text{ones}(N_p,1)$。$A_3$可以由如下的算法2得到。Maximum matching ${\mathbf{z}}^{\ast }={\text{argmax}}_{\mathbf{z}}({\mathbf{c}}^T\mathbf{z})$。

1. 最大抓捕数$q$是唯一的，而maximum matching ${\mathbf{z}}^{\ast }$可能有多个解。原问题是一个带有$(2^{N_p}-1)\times N_e$个约束的二分匹配问题，是一个NP问题。但是通过定理5求解的问题相较于原问题被大幅简化，只具有$N_v$个变量和$N_v+N_e+N_p$个不等式约束。如果$\mathbf{r}$具有很多零元素，则式（50）中的第一个不等式约束还会更加简化。

定义10（Maximum Matching Pairs）：对于一个maximum matching ${\mathbf{z}}^{\ast }=[{\mathbf{s}}^{1\ast },{\mathbf{s}}^{2\ast }{]}^T$，定义如下的matching pairs的集合，分别用来表示所有一对一的matching pairs和二对一的matching pairs。

$$\begin{array}{rl}{M}^1({\mathbf{z}}^{\ast })& =\left\{(i,j)|s_i^{1\ast }(j)=1,1\le i\le N_p,1\le j\le N_e\right\}\\ M^2({\mathbf{z}}^{\ast })& =\{(i1,i2,j)|s_{i1,i2}^{2\ast }(j)=1,1\le i1<i2\le N_p,1\le j\le N_e\}.\end{array}$$

三、仿真结果

假设$\alpha =0.7$，$v_P=1\text{m/s}$，$v_E=0.7\text{m/s}$。

Case 1

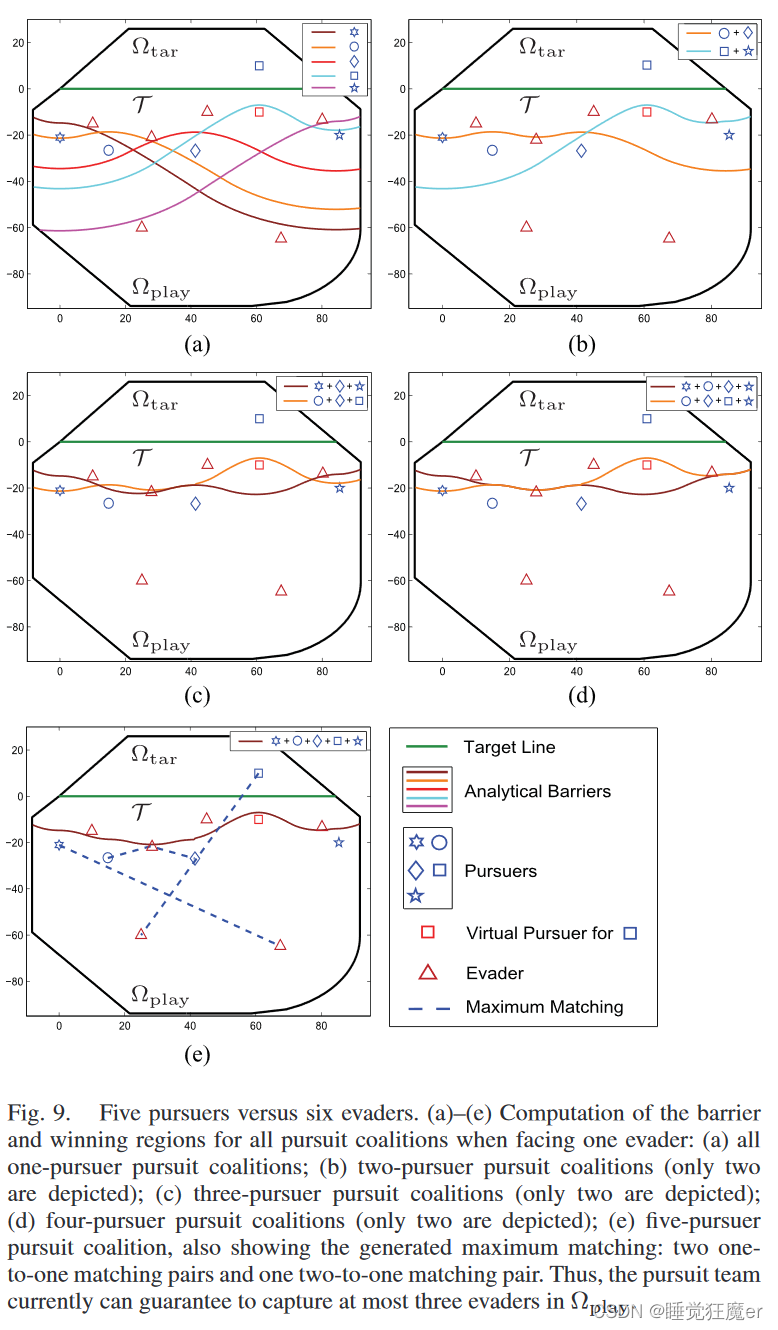
$N_p=5$，$N_e=6$。Fig. 9展示了所有pursuit coalitions的barrier和winning region。Fig. 9(a)-(d)分别展示了包含1-4个pursuers的pursuit coalitions。共计算了31个barriers，耗时0.984s。主要耗时在于计算barriers上的点和计算他们的交集。Fig. 9(e)展示了最终计算的barrier，并计算了计算了maximum matching，包括两个1对1的matching pairs和一个2对1的matching pair。求解0-1规划耗时0.025s。

Case 2

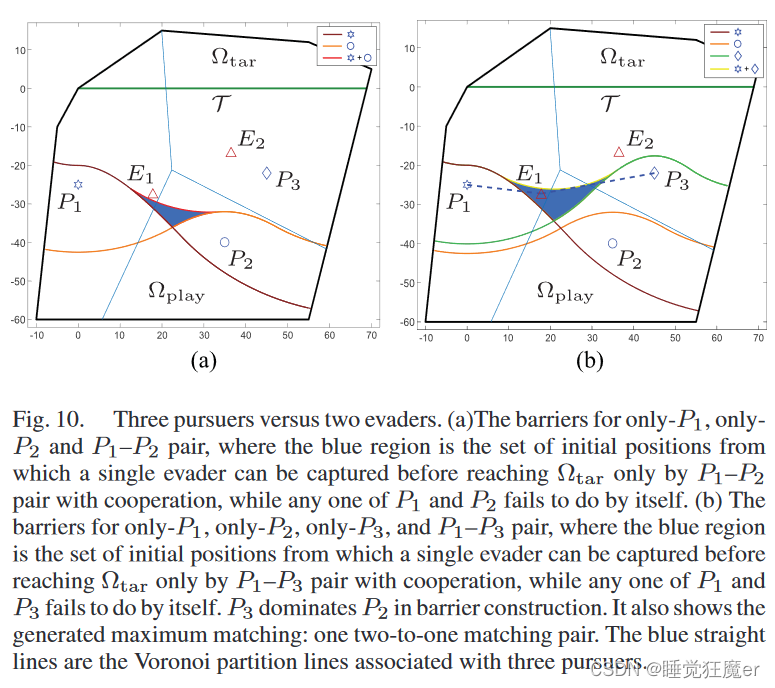
$N_p=3$，$N_e=2$。这个例子是为了说明论文中所述方法不是平凡的（trivial）并且不同于分配两个最近的pursuer到每个evader。Fig. 10(a)给出了仅有$P_1$、仅有$P_2$，$P_1-P_2$的barrier，可以观察到，如果evader初始位于蓝色区域内，则它只能被$P_1-P_2$共同抓捕。在Fig. 10(b)中的情况是类似的，如果evader初始位于蓝色区域内，则它只能被$P_1-P_2-P_3$共同抓捕。

在这种情况下，$E_2$一定能够到达${\Omega }_{\text{tar}}$而$E_1$能够被$P_1-P_3$抓捕。尽管$P_1$和$P_2$都比$P_3$到$E_1$的距离更近，但是$P_3$仍然被分配到了$E_1$。同样的，尽管$P_3$和$P_2$距离$E_2$更近，但是$P_3$仍然被分配到了更远的$E_1$。这说明论文所述方法不是简单地将最近的两个pursuer分配到每个evader。

这种情况计算barriers耗时0.023s，计算maximum matching耗时0.012s。

四、结论

4.1 论文的主要贡献

• 单pursuit coalition对单个evader的barrier的解析计算方法
• 多pursuit coalitions对单个evader的barriers的解析计算方法
• pursuers位于target region时的barrier解析计算方法
• pursuit coalitions到evaders的assignment的0-1规划方法。