一、信道建模


二、MU-MIMO
MU-MIMO(Multi-User MIMO)是一种无线通信技术,允许基站(BS)同时向多个用户设备(UE)发送数据,从而提高系统容量和频谱效率。以下是 MU-MIMO 的数学建模过程,涵盖从发送信号到接收信号的完整链路。
1. 系统模型
假设:
- 基站(BS) 有 N t N_t Nt 根发射天线。
- K 个用户(UE),每个用户有 N r , k N_{r,k} Nr,k 根接收天线(通常 N r , k = 1 N_{r,k} = 1 Nr,k=1 或 2 2 2)。
- 信道矩阵 H k ∈ C N r , k × N t \mathbf{H}_k \in \mathbb{C}^{N_{r,k} \times N_t} Hk∈CNr,k×Nt 表示 BS 到第 k k k 个用户的信道。
- 预编码矩阵 W k ∈ C N t × d k \mathbf{W}_k \in \mathbb{C}^{N_t \times d_k} Wk∈CNt×dk 用于调整发射信号( d k d_k dk 是第 k k k 个用户的数据流数)。
- 发送信号 x k ∈ C d k × 1 \mathbf{x}_k \in \mathbb{C}^{d_k \times 1} xk∈Cdk×1 是第 k k k 个用户的数据符号(如 QAM 符号)。
- 噪声 n k ∈ C N r , k × 1 \mathbf{n}_k \in \mathbb{C}^{N_{r,k} \times 1} nk∈CNr,k×1 是加性高斯白噪声(AWGN), n k ∼ C N ( 0 , σ 2 I ) \mathbf{n}_k \sim \mathcal{CN}(0, \sigma^2 \mathbf{I}) nk∼CN(0,σ2I)。
2. 发送端处理
(1) 预编码(Precoding)
BS 对每个用户的数据进行 线性预编码(如 Zero-Forcing, MMSE),以减少用户间干扰(Inter-User Interference, IUI)。
总发送信号:
s
=
∑
k
=
1
K
W
k
x
k
\mathbf{s} = \sum_{k=1}^K \mathbf{W}_k \mathbf{x}_k
s=k=1∑KWkxk
其中:
- W k \mathbf{W}_k Wk 是第 k k k 个用户的预编码矩阵。
- x k \mathbf{x}_k xk 是第 k k k 个用户的数据符号。
(2) 功率约束
总发射功率受限:
E
[
∥
s
∥
2
]
≤
P
max
\mathbb{E}[\|\mathbf{s}\|^2] \leq P_{\text{max}}
E[∥s∥2]≤Pmax
其中
P
max
P_{\text{max}}
Pmax 是最大发射功率。
3. 信道传输
信号经过无线信道后,第
k
k
k 个用户的接收信号:
y
k
=
H
k
s
+
n
k
\mathbf{y}_k = \mathbf{H}_k \mathbf{s} + \mathbf{n}_k
yk=Hks+nk
代入
s
\mathbf{s}
s:
y
k
=
H
k
W
k
x
k
+
∑
j
≠
k
H
k
W
j
x
j
+
n
k
\mathbf{y}_k = \mathbf{H}_k \mathbf{W}_k \mathbf{x}_k + \sum_{j \neq k} \mathbf{H}_k \mathbf{W}_j \mathbf{x}_j + \mathbf{n}_k
yk=HkWkxk+j=k∑HkWjxj+nk
其中:
- 第一项 H k W k x k \mathbf{H}_k \mathbf{W}_k \mathbf{x}_k HkWkxk 是 期望信号。
- 第二项 ∑ j ≠ k H k W j x j \sum_{j \neq k} \mathbf{H}_k \mathbf{W}_j \mathbf{x}_j ∑j=kHkWjxj 是 用户间干扰(IUI)。
- 第三项 n k \mathbf{n}_k nk 是 噪声。
4. 接收端处理
(1) 检测(Detection)
用户
k
k
k 使用 检测矩阵
G
k
\mathbf{G}_k
Gk(如 MMSE 检测)来恢复数据:
x
^
k
=
G
k
y
k
\hat{\mathbf{x}}_k = \mathbf{G}_k \mathbf{y}_k
x^k=Gkyk
其中:
- G k \mathbf{G}_k Gk 可以是 迫零(ZF)、最小均方误差(MMSE) 或 最大似然(ML) 检测器。
(2) 信干噪比(SINR)
用户
k
k
k 的 SINR(Signal-to-Interference-plus-Noise Ratio):
SINR
k
=
∥
H
k
W
k
∥
2
∑
j
≠
k
∥
H
k
W
j
∥
2
+
σ
2
\text{SINR}_k = \frac{\|\mathbf{H}_k \mathbf{W}_k\|^2}{\sum_{j \neq k} \|\mathbf{H}_k \mathbf{W}_j\|^2 + \sigma^2}
SINRk=∑j=k∥HkWj∥2+σ2∥HkWk∥2
其中:
- 分子是 期望信号功率。
- 分母是 干扰 + 噪声功率。
(3) 可达速率(Achievable Rate)
用户
k
k
k 的 香农容量(Shannon Capacity):
R
k
=
log
2
(
1
+
SINR
k
)
R_k = \log_2 \left( 1 + \text{SINR}_k \right)
Rk=log2(1+SINRk)
5. 预编码方法
(1) 迫零预编码(Zero-Forcing, ZF)
目标:完全消除用户间干扰(IUI)。
预编码矩阵:
W
=
H
H
(
H
H
H
)
−
1
\mathbf{W} = \mathbf{H}^H (\mathbf{H} \mathbf{H}^H)^{-1}
W=HH(HHH)−1
其中
H
=
[
H
1
T
,
H
2
T
,
…
,
H
K
T
]
T
\mathbf{H} = [\mathbf{H}_1^T, \mathbf{H}_2^T, \dots, \mathbf{H}_K^T]^T
H=[H1T,H2T,…,HKT]T 是 联合信道矩阵。
缺点:
- 噪声增强(尤其在信道条件差时)。
- 需要 N t ≥ ∑ k = 1 K N r , k N_t \geq \sum_{k=1}^K N_{r,k} Nt≥∑k=1KNr,k(天线数足够)。
(2) 正则化迫零(Regularized ZF, RZF)
改进 ZF,加入正则化项:
W
=
H
H
(
H
H
H
+
α
I
)
−
1
\mathbf{W} = \mathbf{H}^H (\mathbf{H} \mathbf{H}^H + \alpha \mathbf{I})^{-1}
W=HH(HHH+αI)−1
其中
α
\alpha
α 是正则化因子(平衡干扰消除和噪声增强)。
(3) 最小均方误差(MMSE)预编码
优化目标:最小化 均方误差(MSE):
W
=
H
H
(
H
H
H
+
σ
2
I
)
−
1
\mathbf{W} = \mathbf{H}^H (\mathbf{H} \mathbf{H}^H + \sigma^2 \mathbf{I})^{-1}
W=HH(HHH+σ2I)−1
- 总结
- MU-MIMO 的核心 是 预编码 和 干扰管理。
- ZF 预编码 完全消除干扰,但可能增强噪声。
- MMSE/RZF 预编码 在干扰和噪声之间权衡。
- SINR 和可达速率 是衡量 MU-MIMO 性能的关键指标。
该模型可用于 5G/6G 通信系统 的仿真和优化。

总结一下就是,h1、h2是两个用户的信道矩阵,w1和w2是发送端需要做的beamforming,如果能够满足w1和h2完全正交,此时用户一接收到的信号可以完全消除用户二的干扰。但是,如果h1和h2之间本身的正交性不好,这种寻找完全正交的w的方式会使得原本发送给用户1的信号投影到w1的分量很小!!
MIMO
SVD预编码

MIMO信号检测


Alamouti空时分组编码



空时编码(Space-Time Coding, STC)和MIMO(多输入多输出,Multiple-Input Multiple-Output)是无线通信中密切相关的两种技术,它们共同利用多天线系统提升通信性能。以下是它们的联系和区别:
1. MIMO技术
- 核心思想:通过多根发射天线和接收天线,利用空间维度提升系统性能。
- 主要优势:
- 空间复用:同时传输多个数据流,提高频谱效率。
- 分集增益:通过多路径传输,增强信号可靠性。
- 波束赋形:集中信号能量,提升覆盖范围和信号质量。
2. 空时编码(STC)
- 核心思想:在时间和空间维度上编码信号,利用多根天线传输冗余信息,提升分集增益和可靠性。
- 主要优势:
- 分集增益:通过多天线传输相同信号的不同版本,抵抗信道衰落。
- 编码增益:通过编码设计,提升信号在接收端的分离和检测性能。
3. 空时编码与MIMO的联系
- 空时编码是MIMO的一种实现方式:空时编码利用MIMO的多天线特性,在时间和空间维度上编码信号,实现分集和复用。
- 共同目标:提升系统性能,包括可靠性(分集)和频谱效率(复用)。
- 应用场景:空时编码常用于需要高可靠性的场景(如低速移动或高干扰环境),而MIMO的空间复用则用于高数据速率传输。
4. 空时编码在MIMO中的作用
- 分集增益:通过多天线传输冗余信息,抵抗信道衰落。
- 编码设计:如Alamouti编码,通过正交设计简化接收端信号分离。
- 性能提升:在低信噪比或高干扰环境下,空时编码显著提升系统可靠性。
总结
空时编码是MIMO技术的重要组成部分,利用多天线系统在时间和空间维度上编码信号,提升系统性能。两者共同推动无线通信技术的发展。


多用户MIMO

大规模MIMO


上面的h是指小尺度衰落矩阵。i≠j时写错了应该等于0,。信道硬化是好处!!!!!!还有,这个h是需要在很多多径情况下符合复高斯分布的条件,这个在sub-6G频段上很容易满足,但在毫米波波长很多,多径数很少,因此不满足复高斯分布,所以信道硬化开始消失。


信号处理流程

大规模MIMO信号检测

最大似然检测
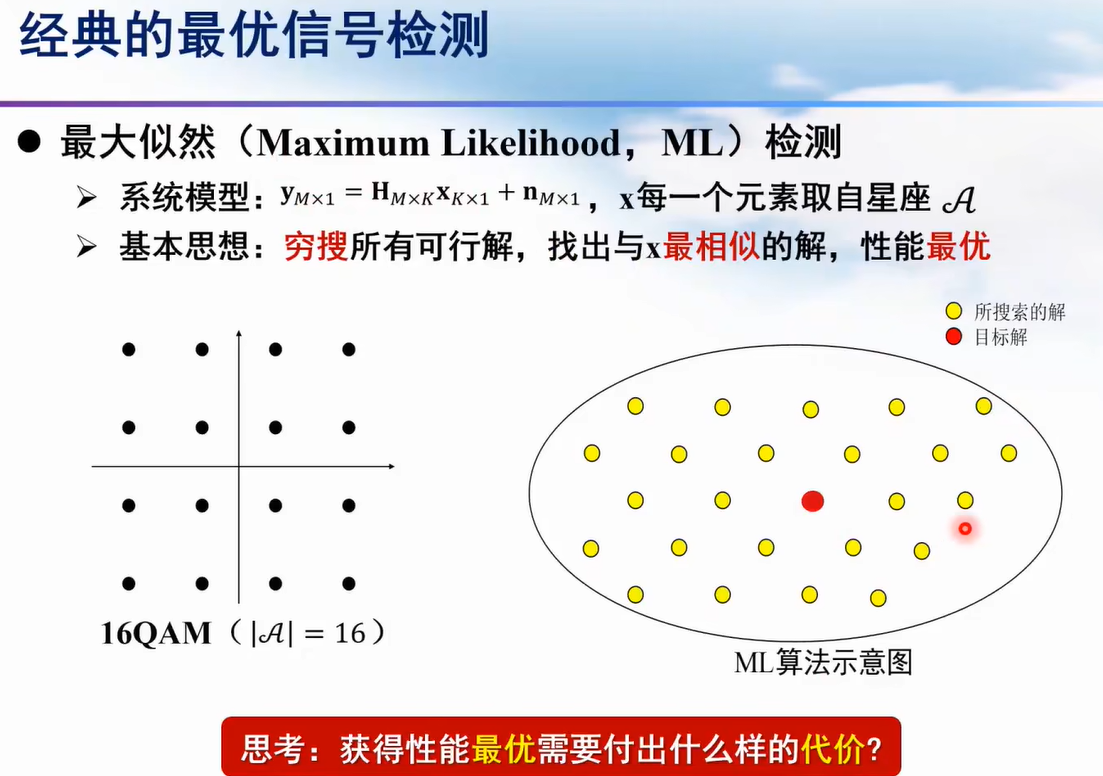
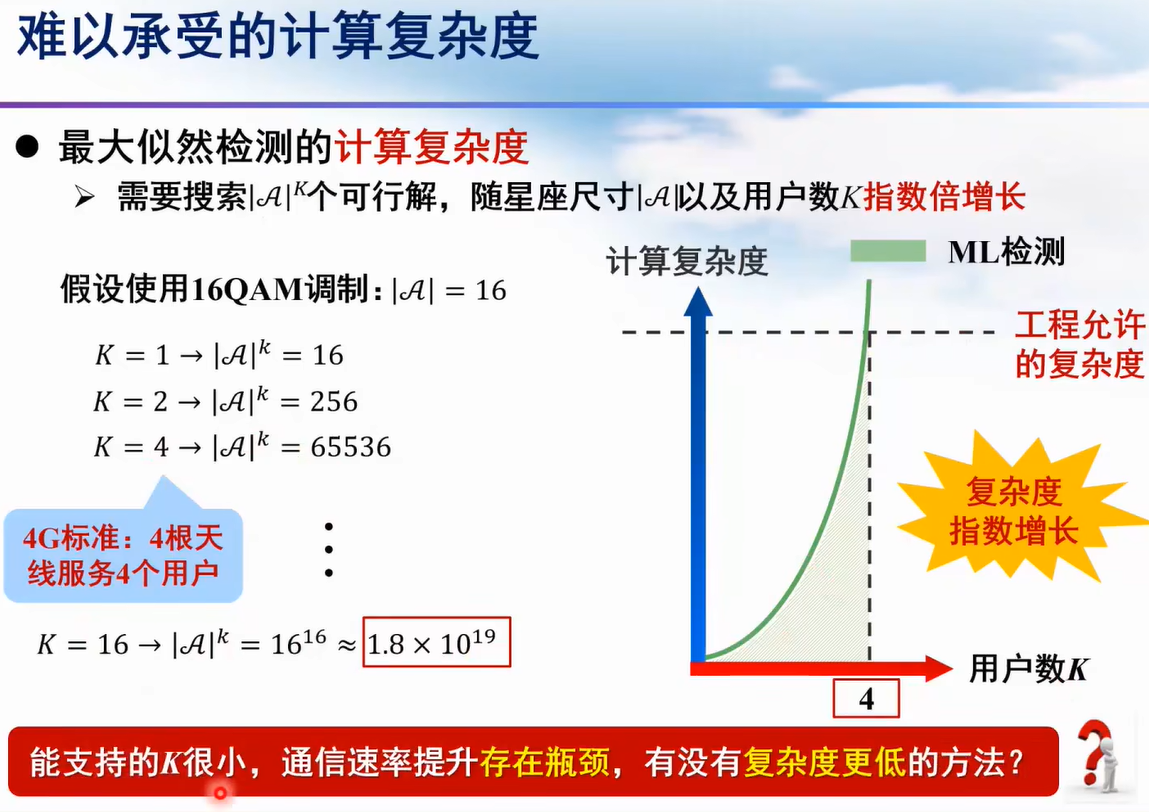
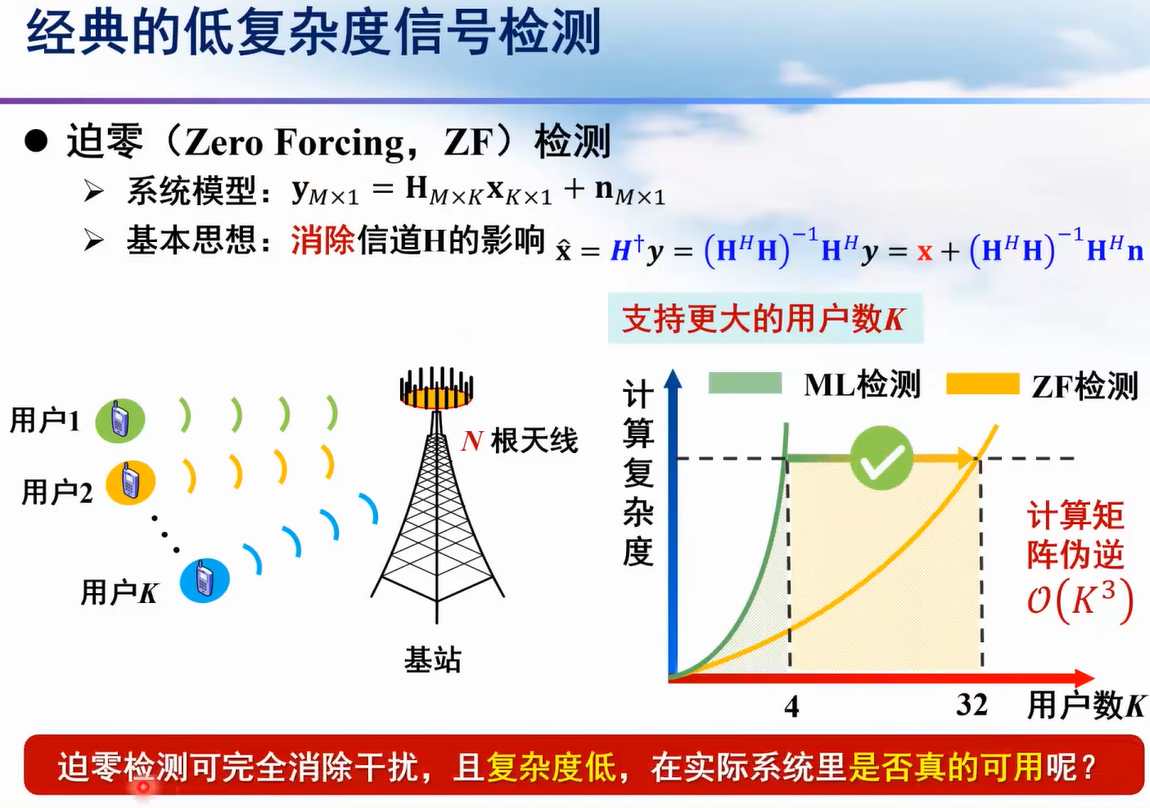
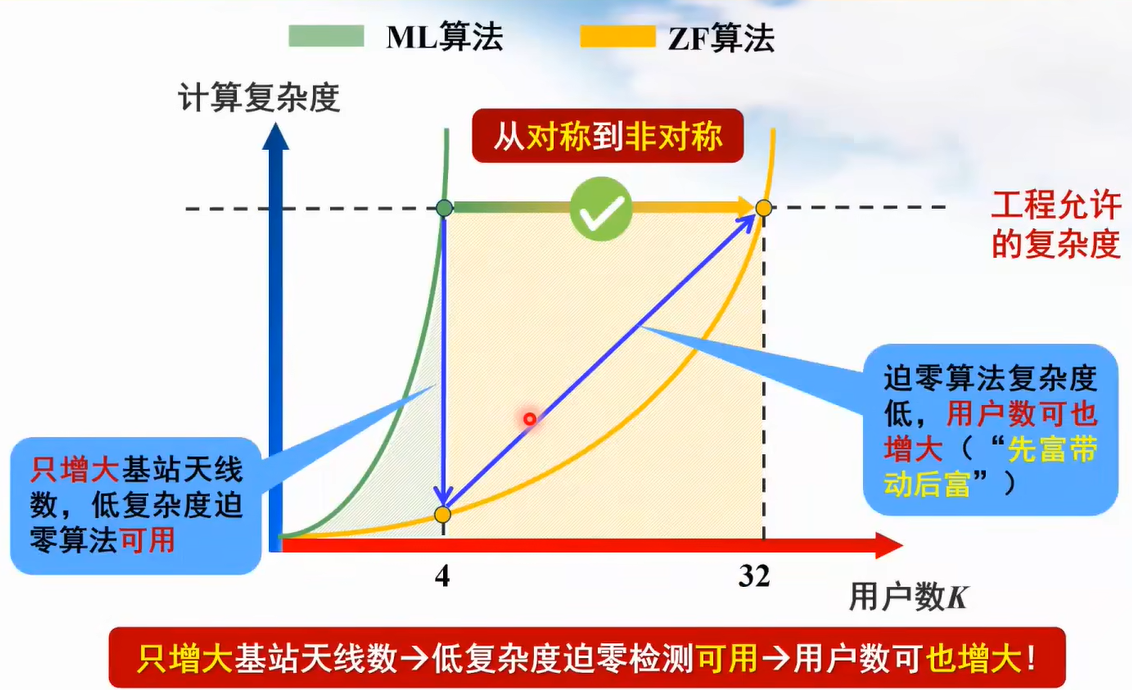
迫零检测




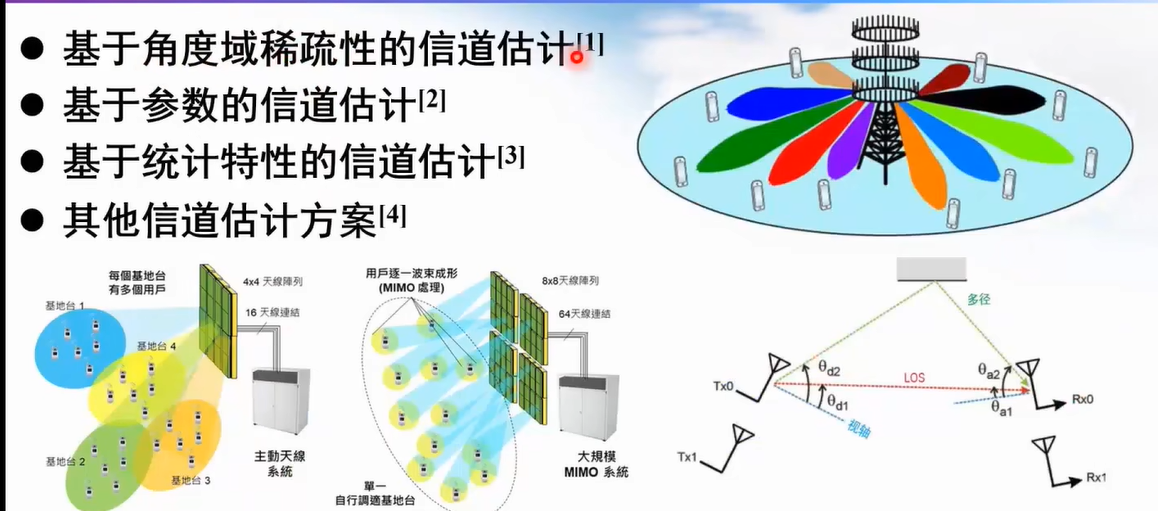
下行信道估计
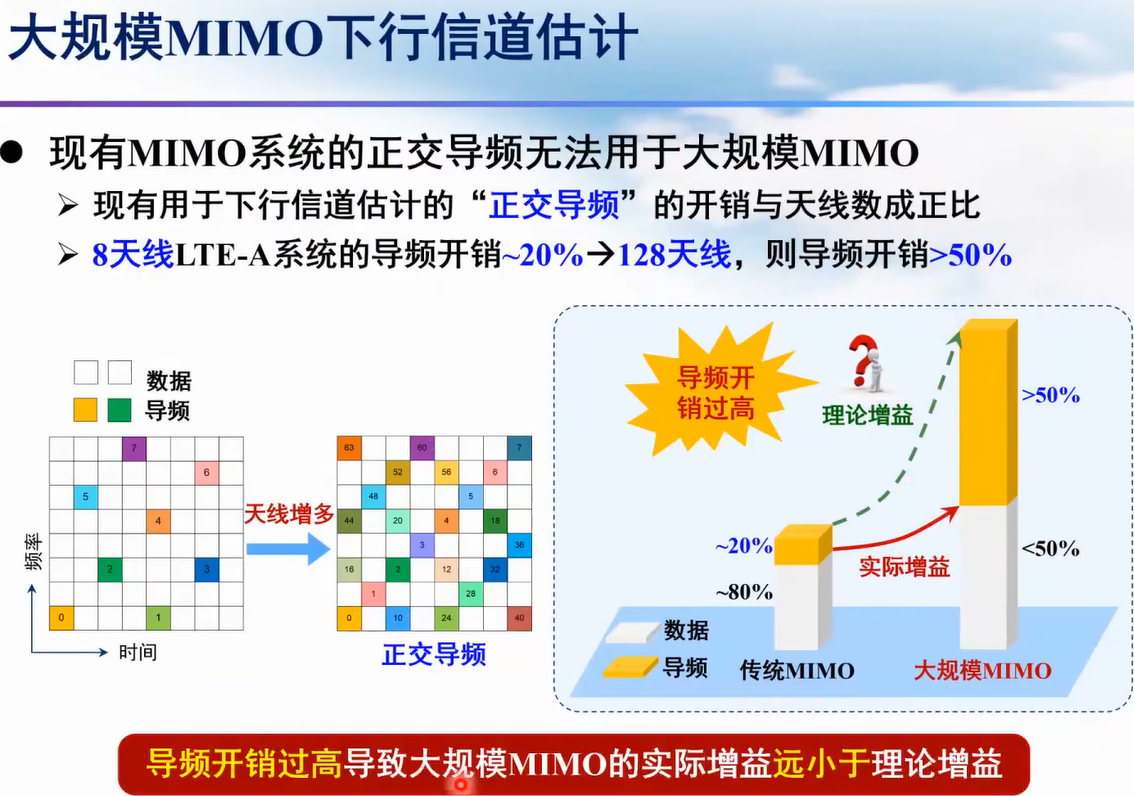



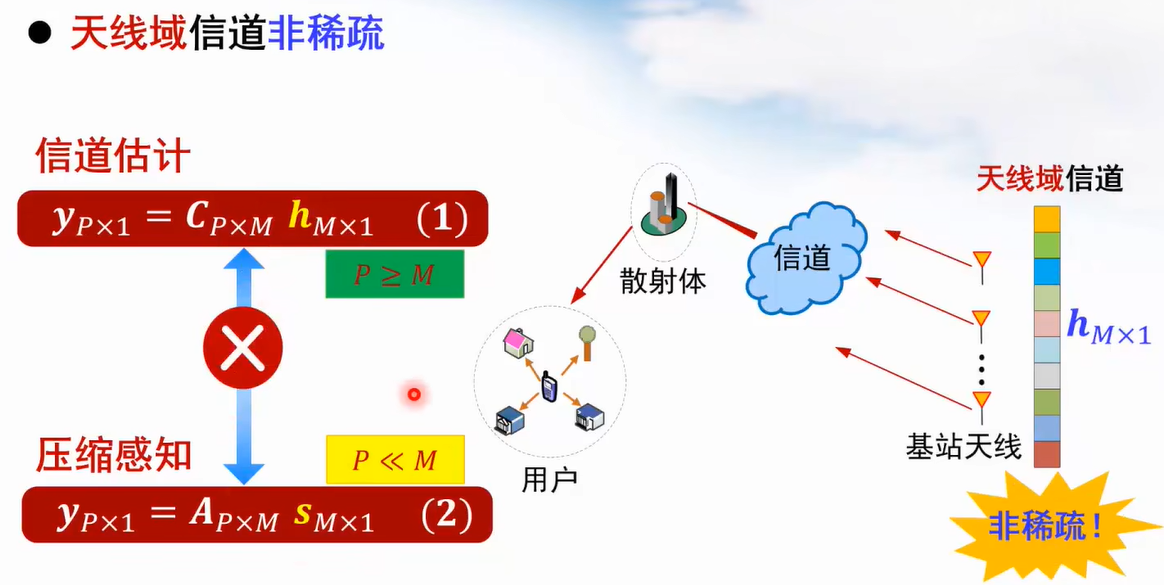
因为每根发射天线都有信号发送,因此并不稀疏。
但是空域可以经过DFT变换到角度域!通过对空域信道向DFT矩阵投影,即可变换为角度域信道


上行信道反馈(基站获取下行信道估计)
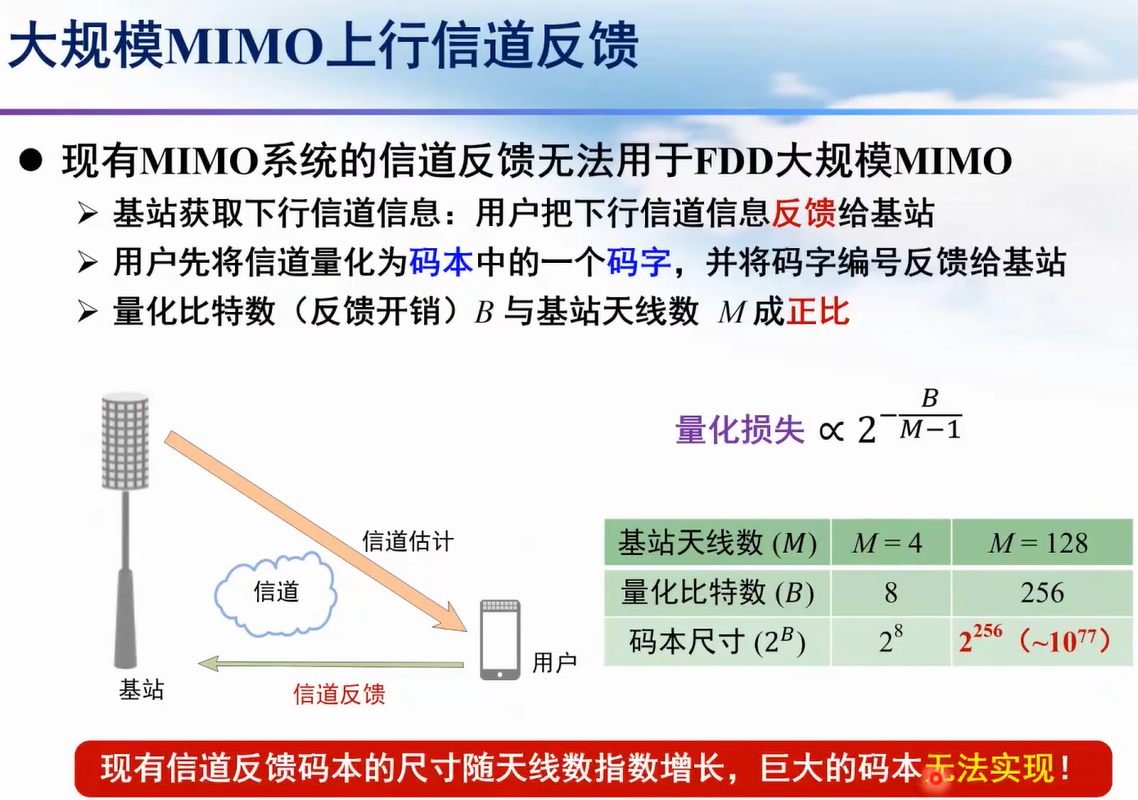
- 假设信道矩阵为 h ∈ C M × 1 \mathbf{h} \in \mathbb{C}^{M \times 1} h∈CM×1(表示 M M M 根天线的信道系数),其维度随 M M M 增大而增加。若每个天线的信道系数需要 b b b 比特量化,则总比特数为 B = M × b B = M \times b B=M×b。 因此,量化比特数 B B B 需要与天线数 M M M 成正比
- 若所有天线共用固定大小的码本(如8个),则每个天线的信道状态仅能用
log
2
8
=
3
\log_2 8 = 3
log28=3 比特描述,但实际需要的比特数
b
b
b 需满足:
B 总 = M × b ⇒ b = B 总 M B_{\text{总}} = M \times b \quad \Rightarrow \quad b = \frac{B_{\text{总}}}{M} B总=M×b⇒b=MB总
当 M = 128 M=128 M=128 时, b ≈ 0.06 b \approx 0.06 b≈0.06 比特/天线,完全无法描述信道状态。 - 合理的 码本大小公式:
码本大小 = 2 B \text{码本大小} = 2^B 码本大小=2B- 当 B B B 与 M M M 成正比时(如 B = 2 M B=2M B=2M): 码本大小为 2 2 M 2^{2M} 22M,虽然随 M M M 增长,但增长速度是指数级的。
解决方案:如何平衡精度与开销?
虽然
B
∝
M
B \propto M
B∝M 是理论上的必要条件,但直接采用会导致码本爆炸。因此,实际系统中需采用以下优化方法:
1. 稀疏码本(Sparse Codebook)
- 原理:利用信道的稀疏性(如大规模MIMO中信道的稀疏性或结构化特性),用少量比特描述主要信道特征。
- 示例:仅反馈信道的主要路径(如强反射路径)而非全部天线信息。
2. 压缩感知(Compressed Sensing)
- 原理:通过随机投影将高维信道向量压缩为低维信号,再通过稀疏表示重建信道。
- 优势:反馈比特数 B ∝ K log ( M ) B \propto K \log(M) B∝Klog(M),而非 M M M,其中 K K K 是信道的稀疏度。
3. 量化与反馈联合优化
- 动态比特分配:根据信道重要性分配比特(如重要路径用更多比特)。
- 反馈压缩算法:结合AI模型(如神经网络)预测信道变化,减少反馈频率。




毫米波大规模MIMO

注意,这里的K表示单天线的用户数量,如果是多天线的情况,直接再乘以天线数就可以了。

超大规模MIMO

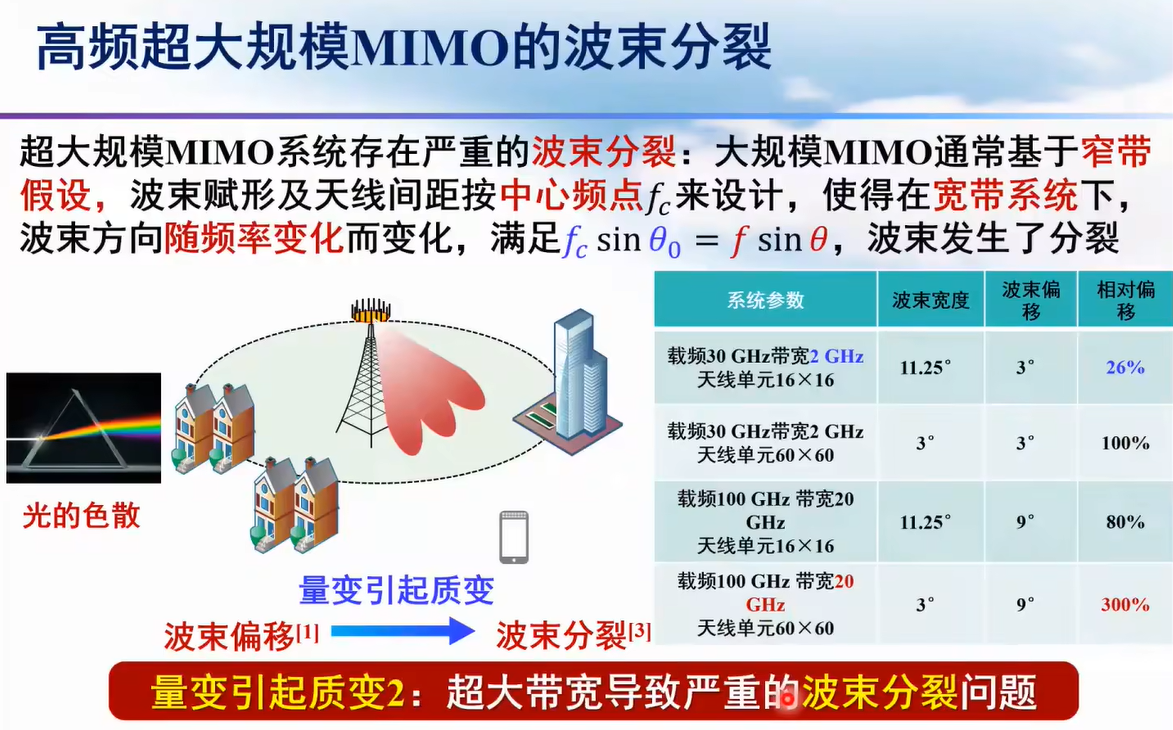


大规模MIMO在低频段通过增加多流数据的传输,实现空分复用,从而提升频谱效率;而在高频段的作用是形成高增益的载波数,克服传输距离短的问题。

























 617
617

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








