本文接着上一篇博弈论 之 1 什么是博弈论_水w的博客-CSDN博客
目录
(1)One not-so-weak Nash equilibrium
回顾:
➢举例: AlphaGo
一个完全信息广泛形式的博弈
- 两名棋手按顺序移动,且每个棋手拥有相同的信息;
- 以博弈树的形式展示和分析该博弈;
- 一种常见的策略是逆向归纳法,即从博弈树的末端开始进行时间上的逆向推理;
- 但该游戏有250^150种可能的走法;
- AlphaGo利用基于卷积神经网络的深度强化学习,并结合蒙特卡洛树搜索;
➢博弈表示方法
人们需要对这个游戏有所了解:
- 玩家是谁
- 玩家可以采取哪些行动
- 每个参与者对每个结果的重视程度
- 每个玩家所知道的内容
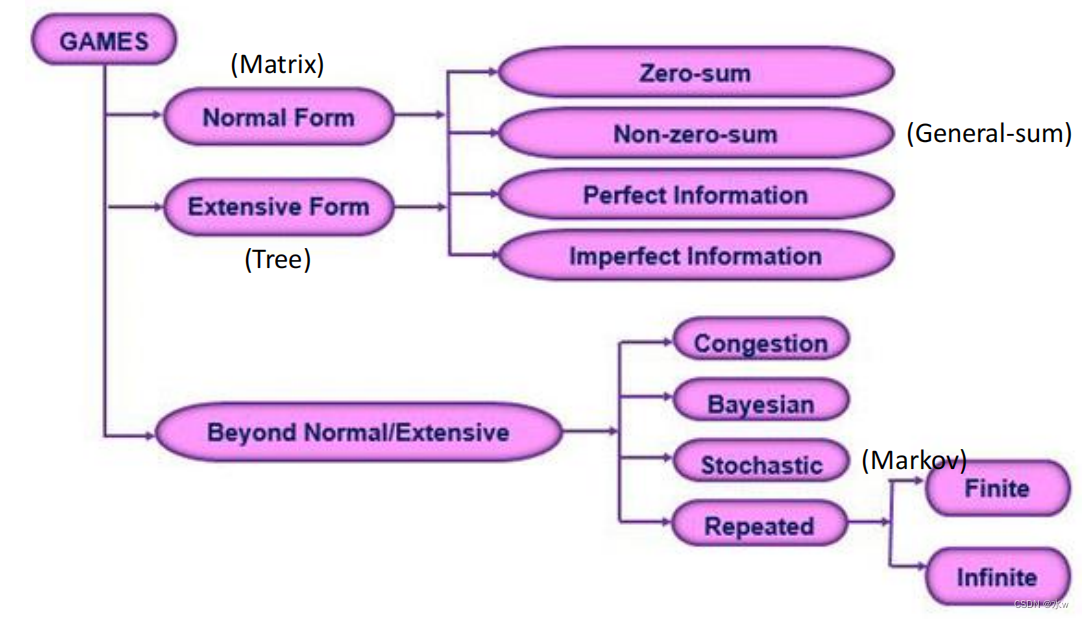
以上信息的正式表示有两种方式:
- 标准形式(或策略形式)表示形式,通过使用参与者的策略总结上述信息
- 广泛形式表示,利用博弈树和信息集对上述信息进行明确描述
➢扩展型博弈
用树形图的形式表示一个博弈
- 标准形式的游戏(矩阵)表示不包含任何顺序、时间和玩家行动的概念;
- 规范形式的游戏代表静态游戏,玩家可以同时选择自己的行动;
- 广泛形式游戏的表现可以,在树中也是如此;
- 广泛型游戏代表动态游戏,即玩家在确定的时间顺序中选择自己的行动;
博弈树
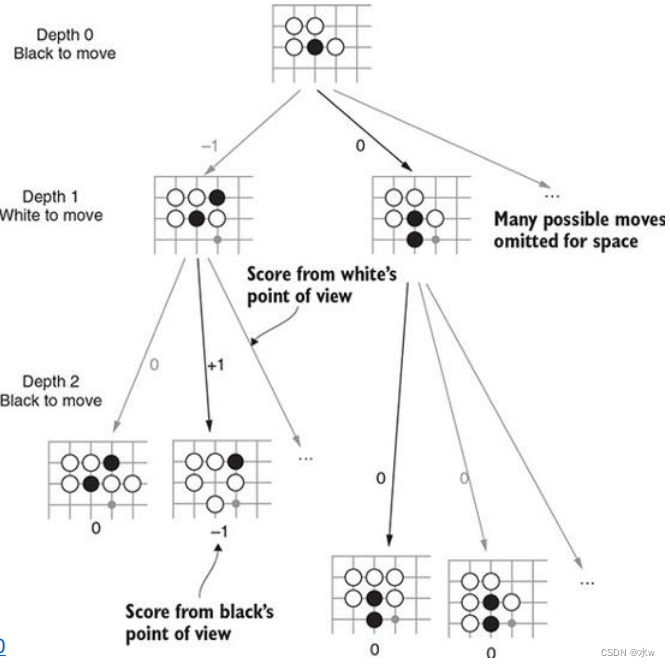
考虑双人回合制游戏:一字棋、西洋跳棋、国际象棋、围棋等。将游戏描述为搜索问题,搜索树可以用来找到下一步行动吗?

两个人,MAX和MIN:
- MAX先动,MIN先动;
- 他们轮流行动,直到比赛结束;
- 比赛结束时,胜者得积分,败者罚点球;
- 初始状态、动作和结果函数为博弈定义博弈树,其中节点为博弈状态,边缘为移动;
➢举例: Tic-Tac-Toe
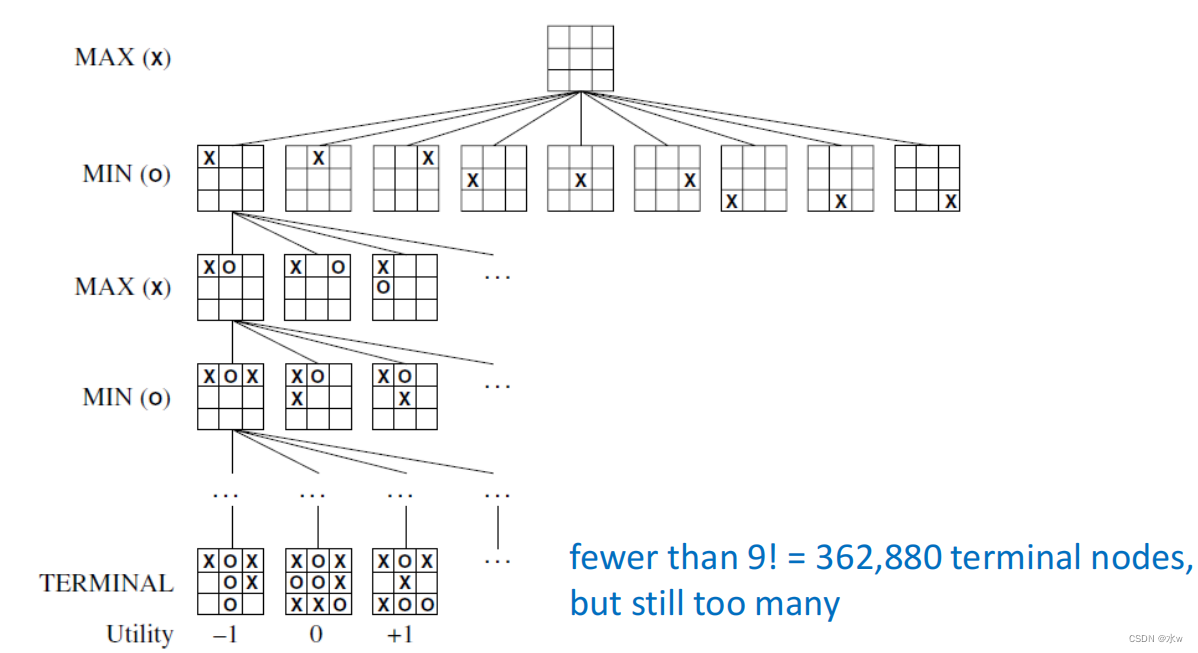
➢MAX纯策略
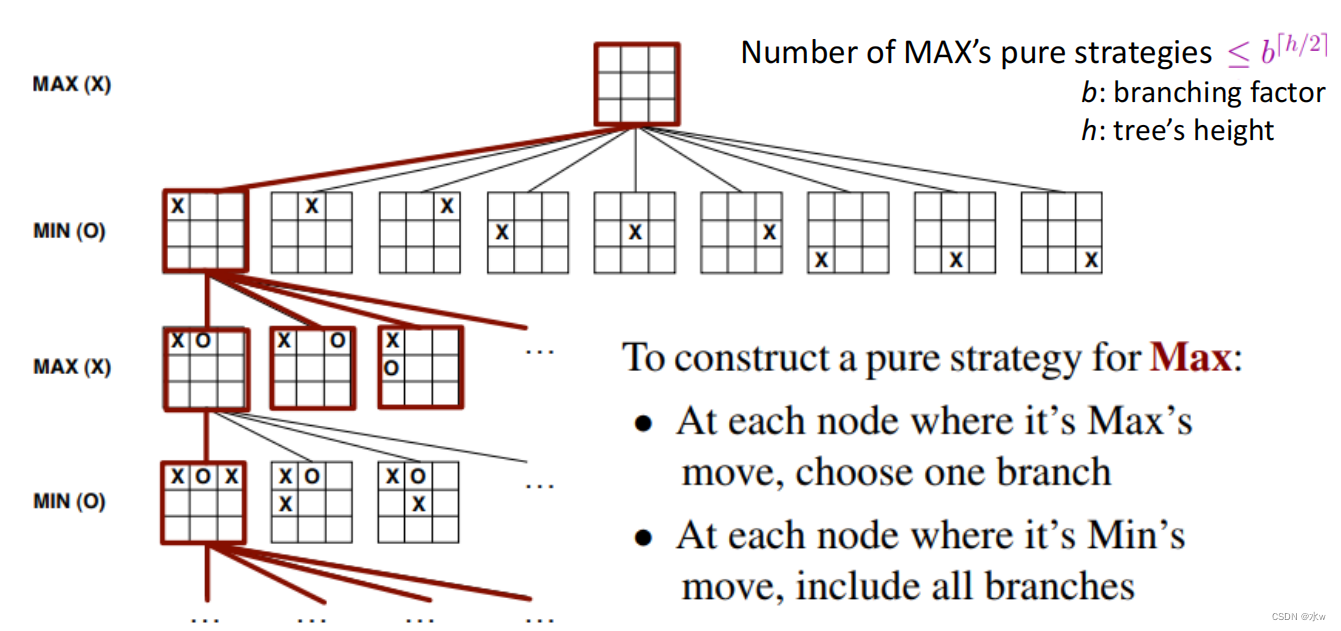
➢MIN纯策略
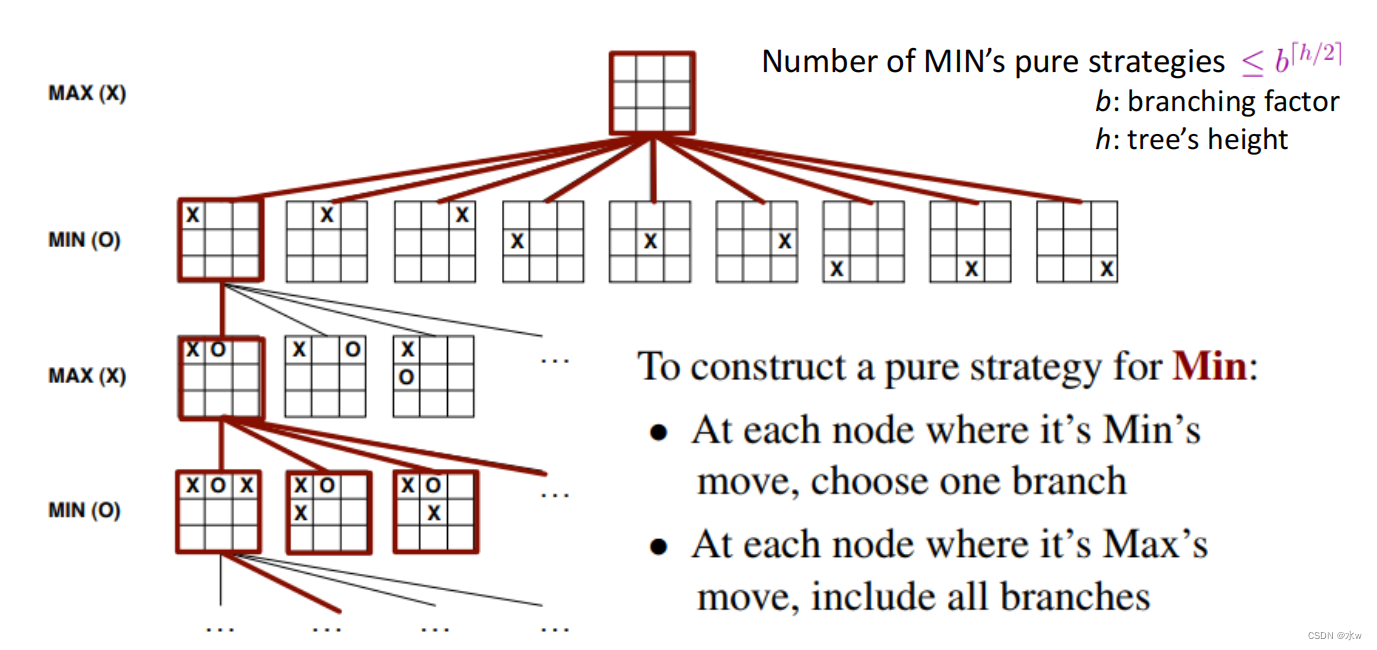
➢最优策略搜索
蛮力搜索策略
- 构造了MAX的纯策略集S和MIN的纯策略集T;
- 根据最大期望效用u(s,t)•复杂度分析选择最佳策略;
- 空间/时间复杂度为
,因为
策略需要构建和存储,每个
策略都是一棵节点树;
如果双方都采用最优策略,这场零和游戏将以平局结束
- 每个参与人都有阻止另一个参与人获胜的策略;
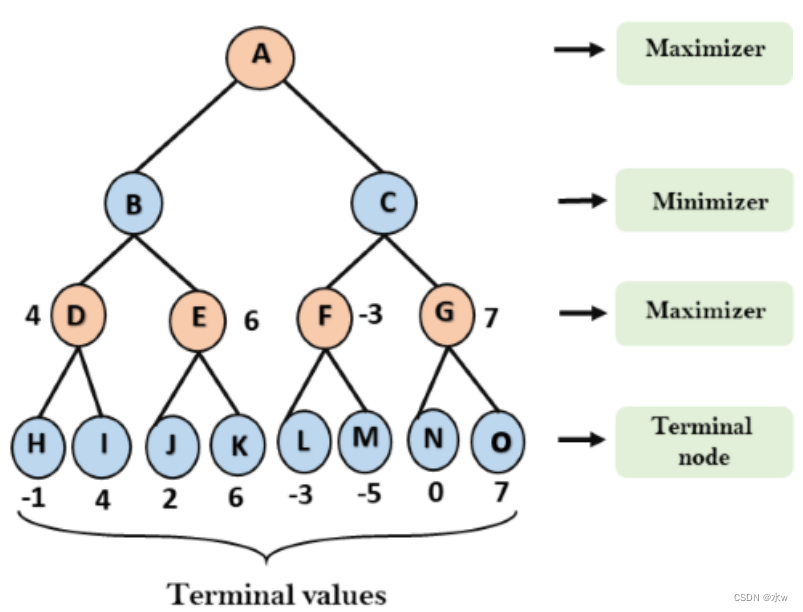
➢Minimax搜索算法
- MAX偏好最大值状态,而MIN偏好最小值状态
- Minimax是一种回溯算法
- 它对游戏树进行深度优先的探索
- 递归一直到树的叶子,同时,极大极小值在树中备份

eg:
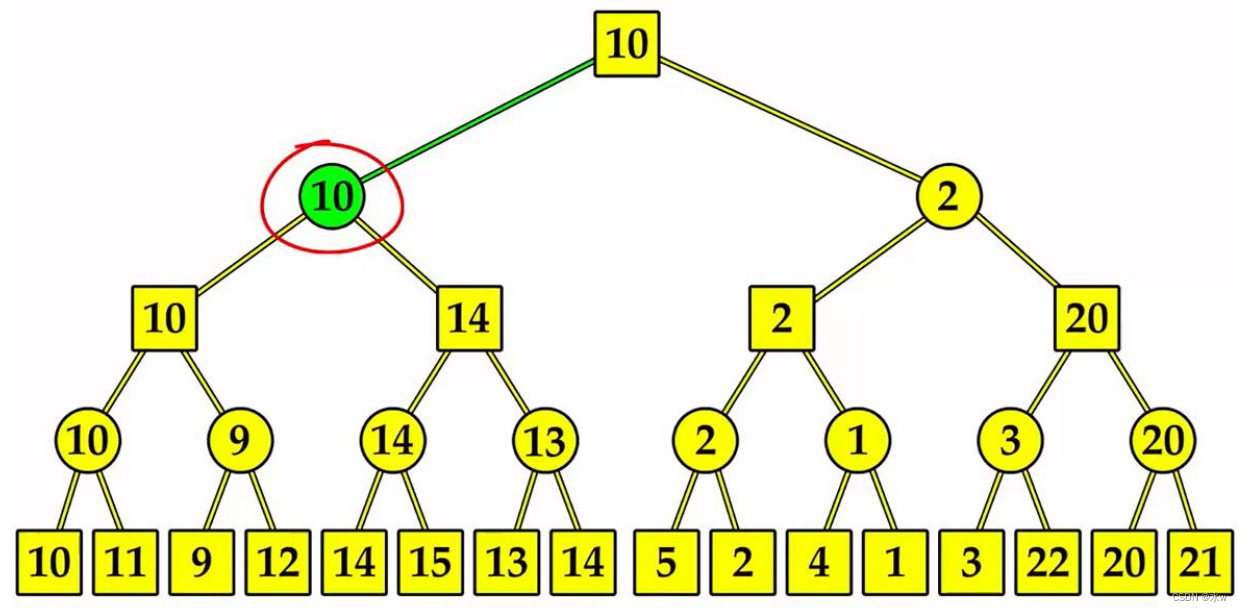
这个算法的问题在于,它需要检查的博弈状态的数量在树的深度上呈指数级增长
- 然而,不需要查看树中的每个节点就可以计算出正确的极大极小决策;
- 修剪的想法可以用来从考虑中消除树的许多分支;
➢什么时候可以剪枝
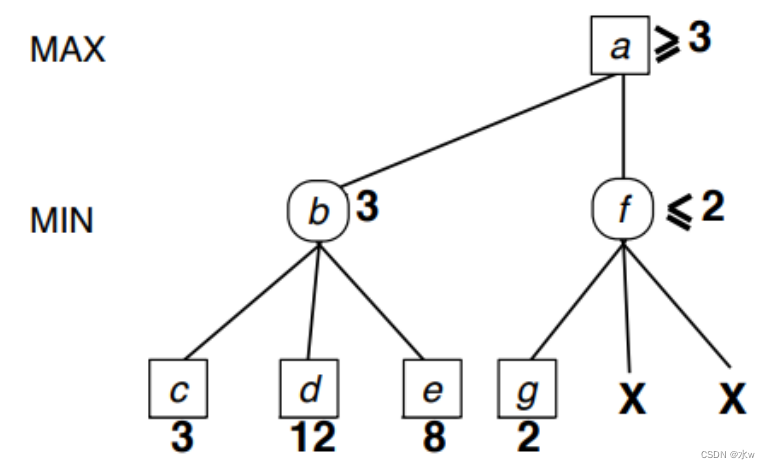
此时, MAX永远不会到f,因为MAX通过到b会得到更高的效用。
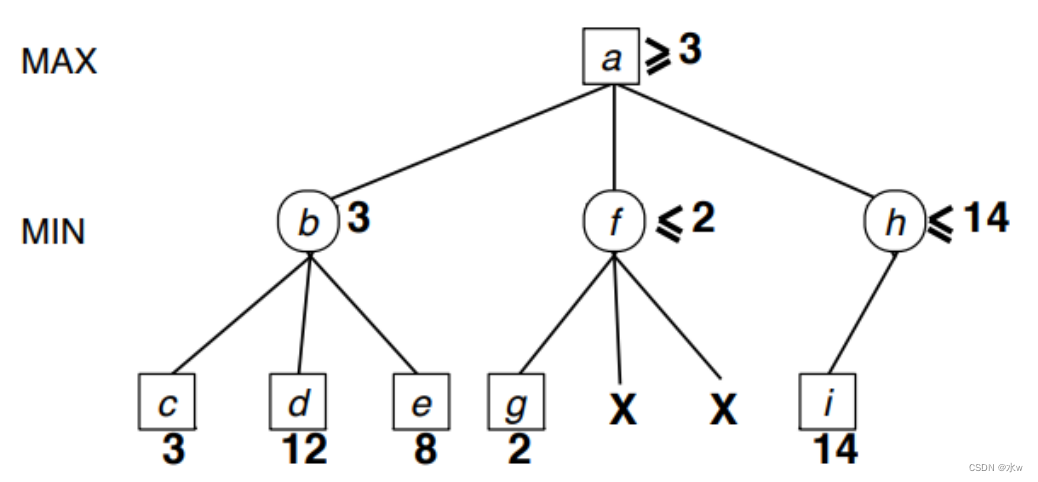
此时,我们不知道h比b好还是差,所以继续。
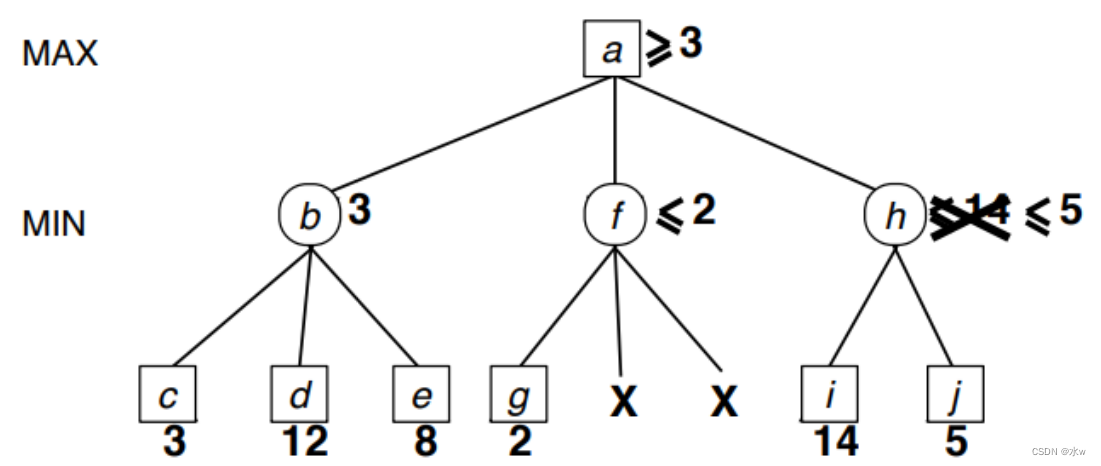
此时,我们还是不知道h比b好还是差,所以继续。
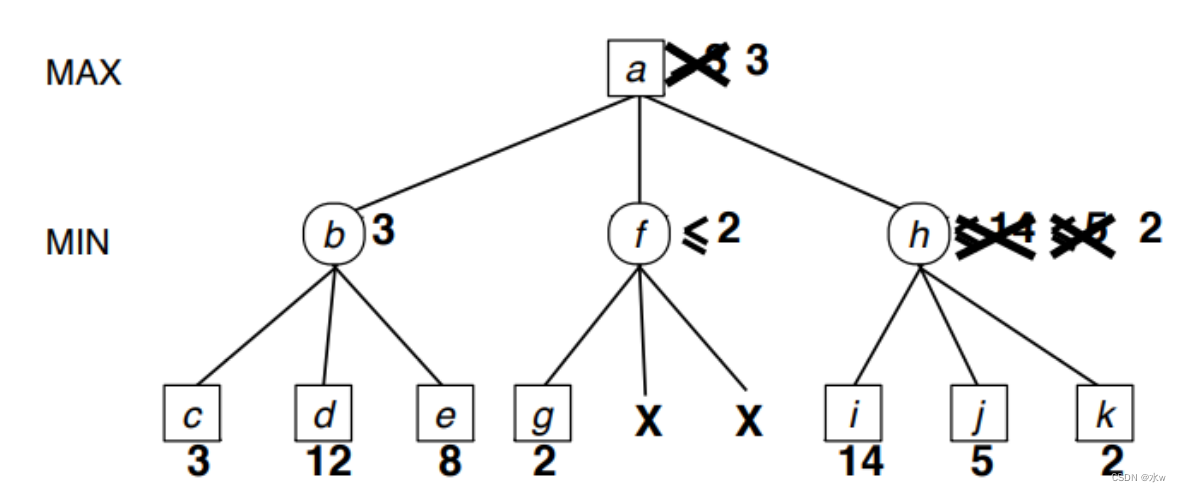
此时,我们可以得出结论,h比b差,并且没有进行修剪。
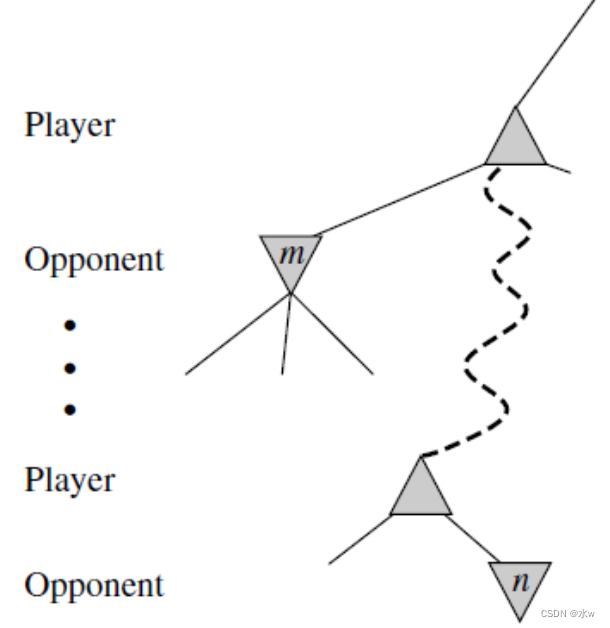
➢Alpha-Beta剪枝算法
Alpha-Beta剪枝是Minimax算法的一种优化技术
- 它返回与标准算法相同的一步,但它删除了所有不影响最终决策的节点;
- 假设树中的某个节点n,玩家可以选择移动到该节点;
- 如果参与人有一个更好的选择m,要么在父节点n,要么在上面的任何一个点,那么节点n在实际游戏中永远不会到;
- 一旦我们对n有了足够的了解(通过检查它的一些后代),得出这个结论,我们就可以修剪它;
- 两个参数描述了备份值在路径上任意位置的边界:
- α =目前为止我们在MAX路径上的任何一个选择点上所发现的最佳(即最高价值)选择的价值;
- β =目前为止我们在最小值路径上的任何一个选择点上所发现的最佳(即最低值)选择的价值;
- Alpha-Beta搜索在执行过程中更新α和β的值,并在已知当前节点的值小于MAX或MIN的α或β的当前值时,删除节点上的剩余分支(即终止递归调用);
伪代码:

一些要点:
- 每个节点更新或复制三个值:节点值、α值和β值;
- MAX只更新α,并试图使α变大。MIN只更新β,并尽量使其更小;
- 如果某个节点α≥β,则修剪剩余的分支,因为最大化(或最小化)父节点可以保证在另一个分支上有更高(或更低)的值;
- 在回溯树时,将节点的值传递给上级节点,而不是α和β的值;
- α和β的值只传递给子节点;
eg:
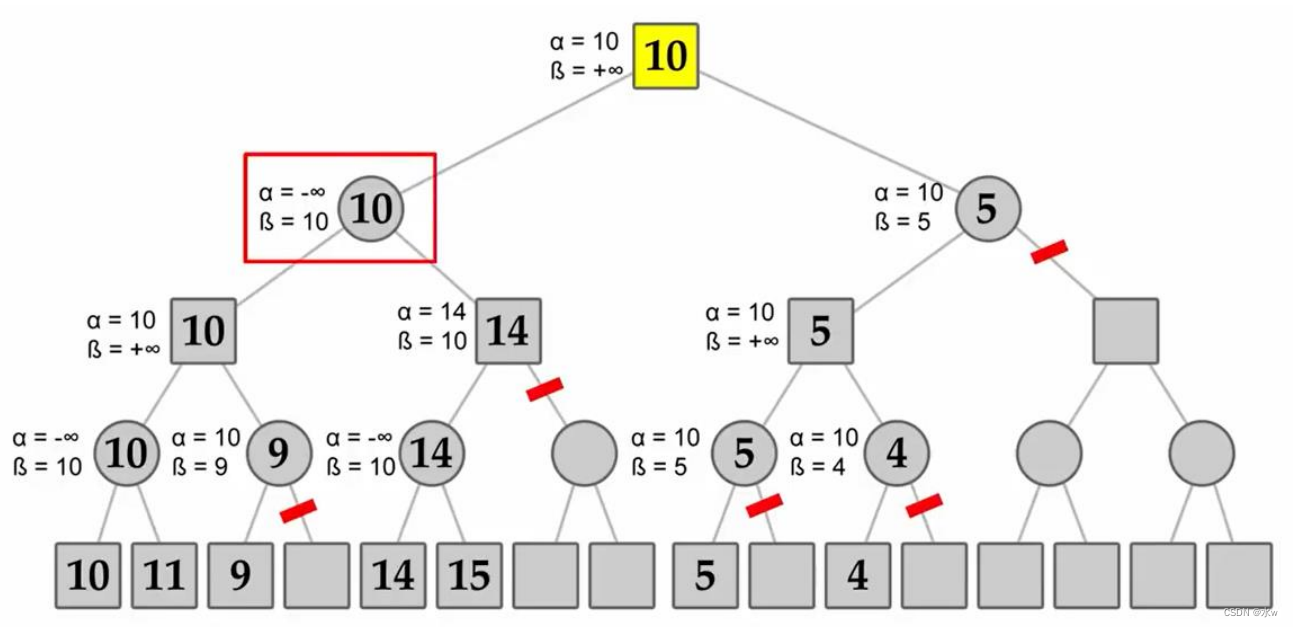
Alpha-Beta修剪受到探索分支的顺序的强烈影响,改进的分支顺序可以指数级地减少要搜索的节点数量。
- 最坏的排序
- 每个参与人的最佳移动发生在树的最右边,这样就不会修剪任何节点;
- 时间复杂度
,工作原理与标准Minimax算法相似;
- 最好的排序
- 每个参与人的最佳移动发生在树的最左边,这样许多节点被修剪;
- 时间复杂度为
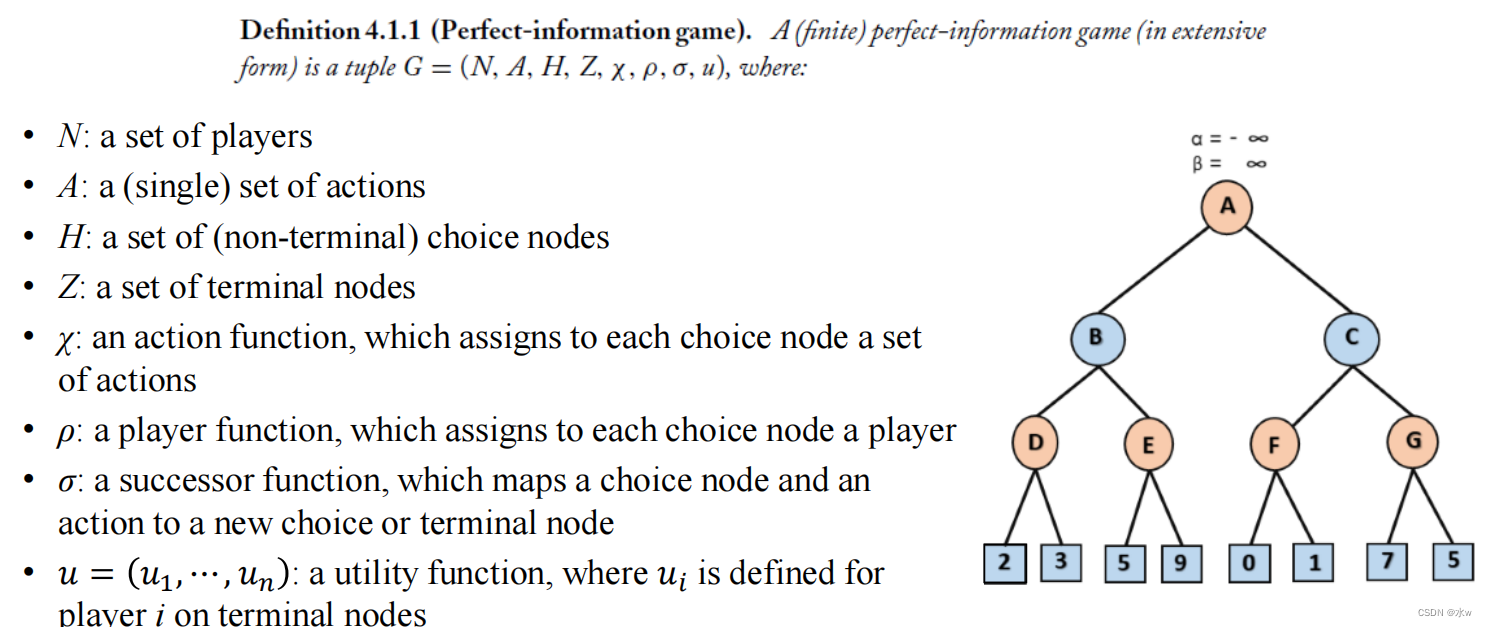
完美信息的扩展型博弈
- N:玩家集合;
- A:一组(单一)动作;
- H:一组(非终端)选择节点;
- Z:终端节点集;
- χ:一个动作函数,它分配给每个选择节点一组动作;
- ρ:一个参与者函数,它给每个选择节点分配一个参与者;
- σ:后继函数,将选择节点和动作映射到新的选择或终端节点;
- 𝑢=𝑢1,⋯,𝑢𝑛:一个效用函数,其中𝑢𝑖is为终端节点上的玩家i定义;
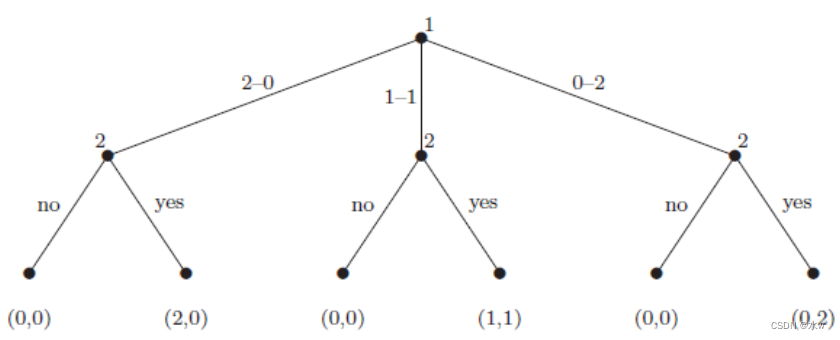
举例: 分享博弈
双人广泛形式游戏
(一)兄弟姐妹按照约定分享父母送给他们的两份不可分割且完全相同的礼物
(三)兄弟首先建议分开:他两个都留,她两个都留,或者两人各留一个
(三)女方可选择接受或拒绝离婚
➢博弈纯策略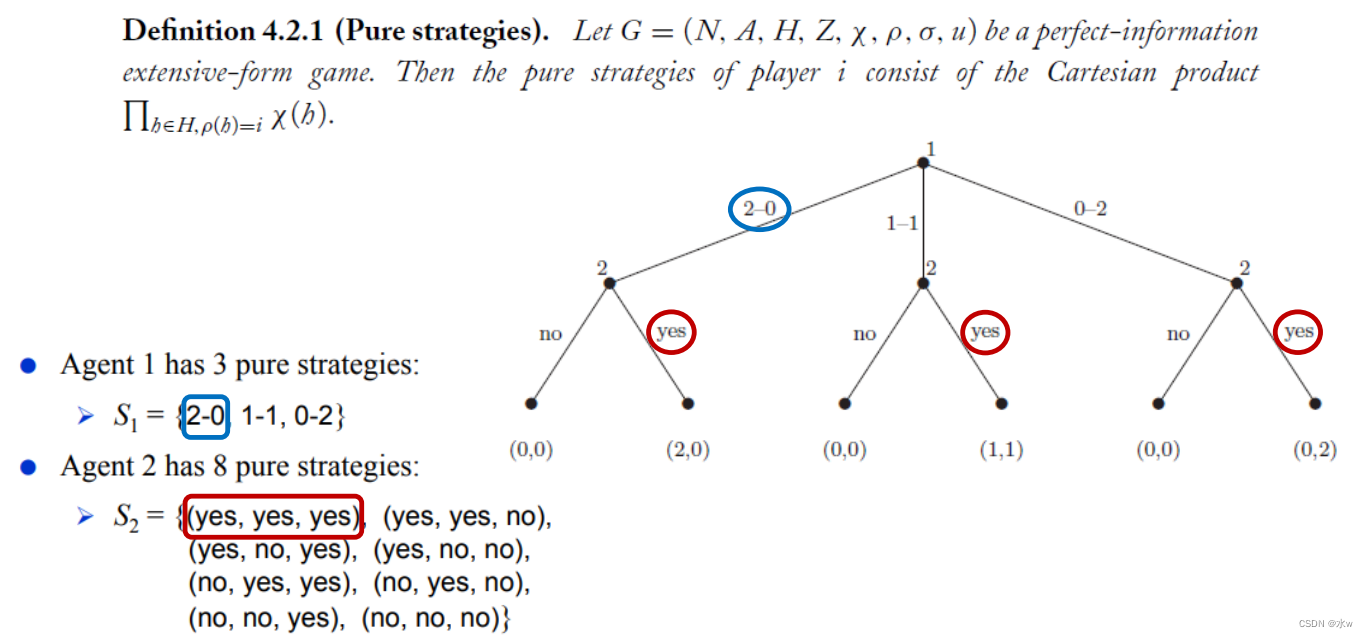
➢扩展型转化为正则型
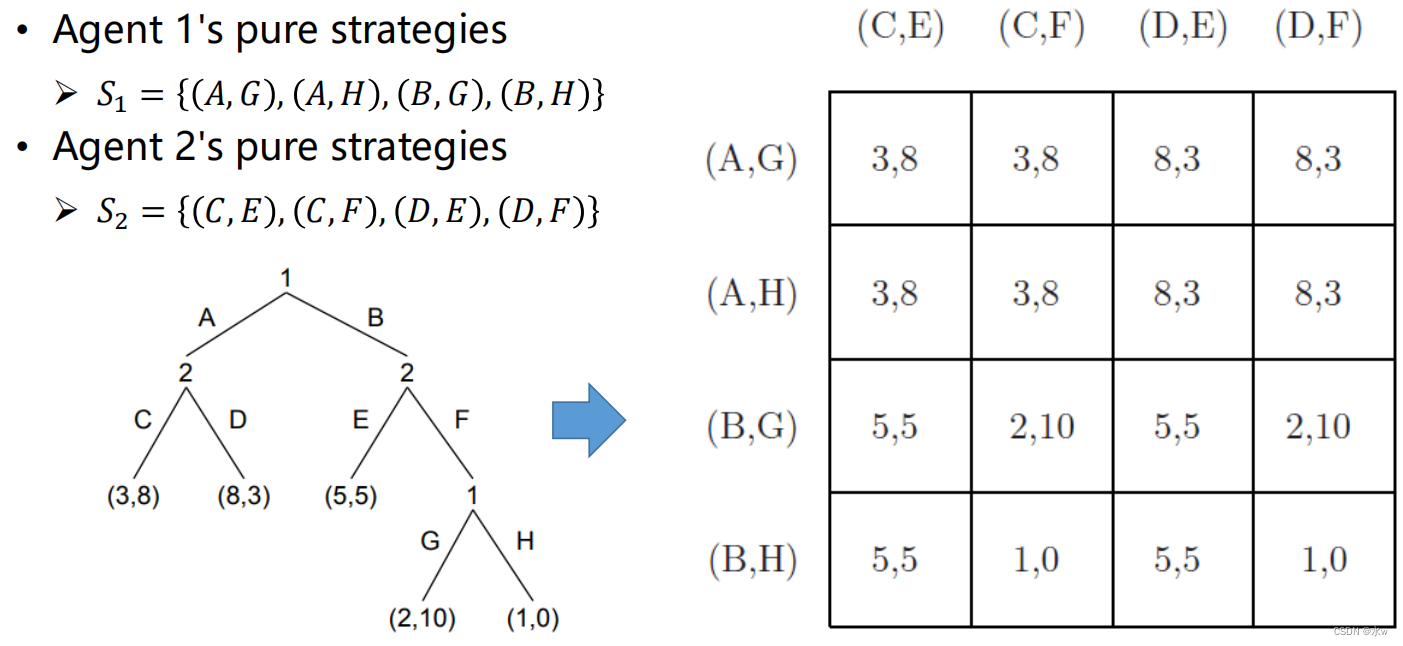
对于每一个完全信息博弈,都存在一个对应的正规型博弈,但存在一定的冗余。然而,从标准形式游戏到广泛形式游戏的反向转换并不总是存在。
➢纳什均衡存在定理

回想一下,这对于普通形式的游戏可能不成立,在这种游戏中,个体会同时采取行动。
- 代理在广泛形式的游戏中轮流移动,所以每个人都可以在移动之前看到目前发生的一切;
- 没有必要为了找到纳什均衡而在行动选择中引入随机性;
- 直觉和定理将不再适用于更一般的博弈,如不完全信息广义博弈;
➢扩展型博弈的纳什均衡
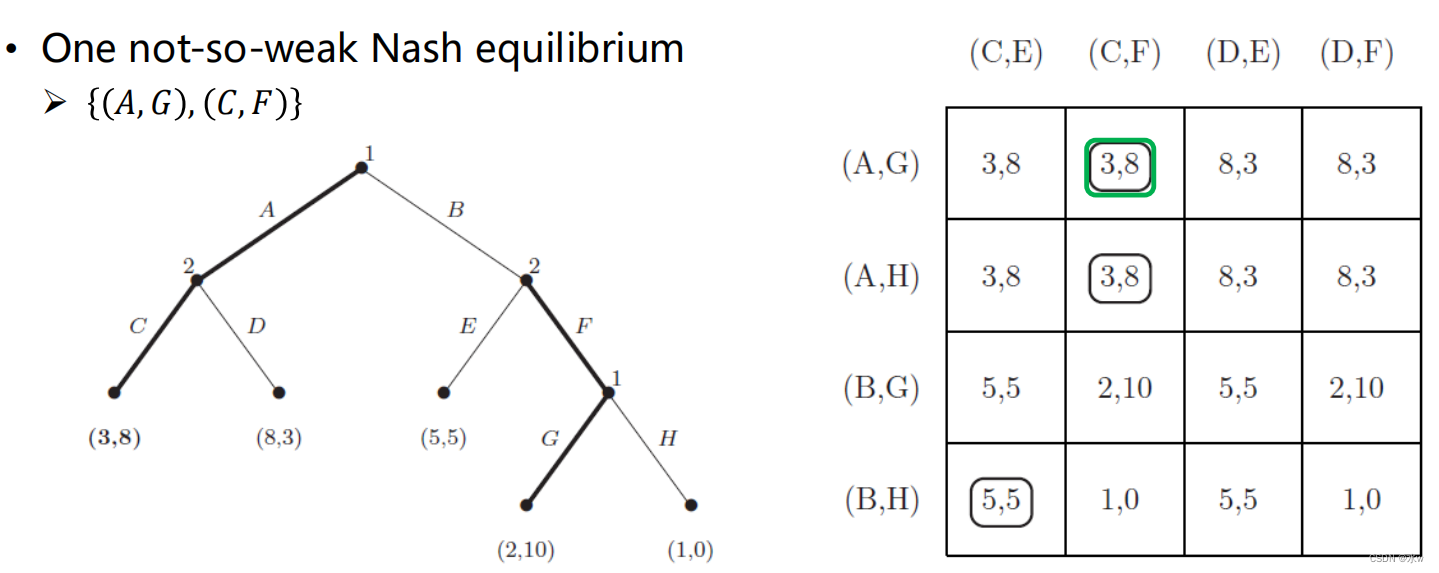
在这个广义博弈中存在三个纯策略纳什均衡
(1)One not-so-weak Nash equilibrium
(2)Two weak Nash equilibria
对于广义博弈来说,纳什均衡的概念太弱了。
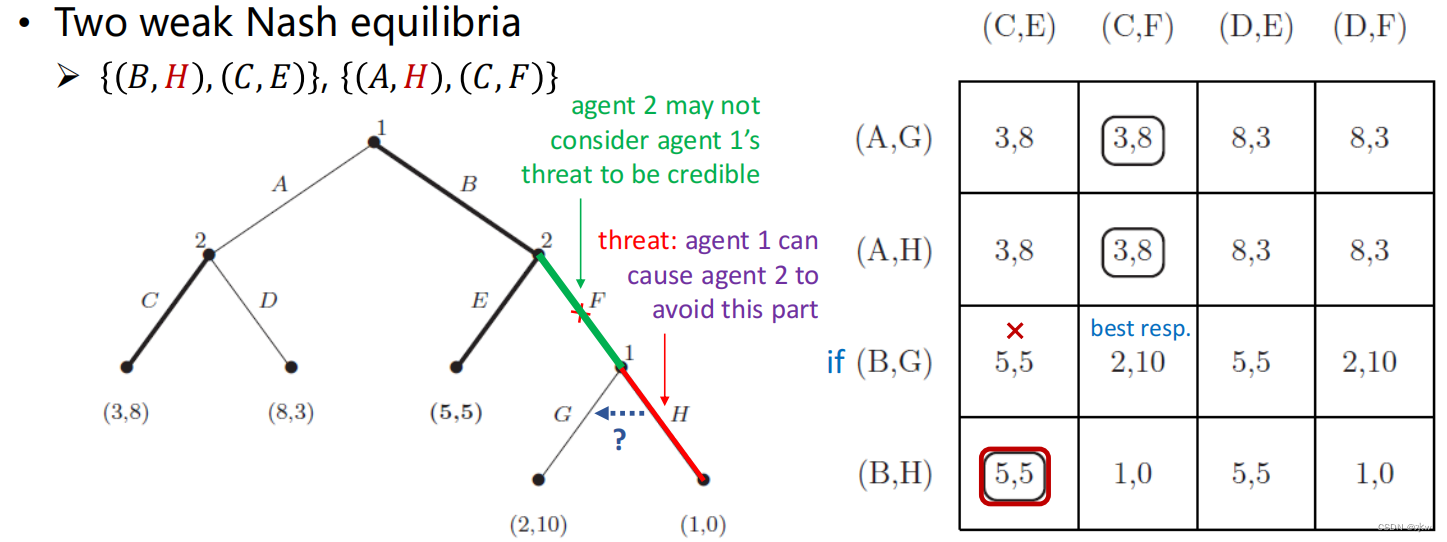
➢子博弈精炼均衡

- 子博弈是任何包含初始节点及其所有后续节点的博弈的子集;
- 游戏G是它自己的子游戏;
次博弈完美均衡的概念是对完全信息广义博弈中纳什均衡的改进,它消除了不需要的纳什均衡;
每个子博弈完美均衡也是纳什均衡,因为博弈G是它自己的子博弈;
但并不是每个纳什均衡都是次博弈完美均衡(也就是说,SPE比NE更强);
每个完全信息广义博弈至少有一个次博弈完美均衡;
次博弈完美均衡的定义排除了“不可信的威胁”,考虑植根于agent 1第二选择节点的子博弈。
- G严格优于H;
- 本博弈的唯一纳什均衡为agent 1参与博弈;
- H在此子博弈中不是最优的,且不能成为原博弈的子博弈完美均衡的一部分;
- 这个不包括
;
➢逆向归纳法
我们可以用逆向归纳法找到次博弈完美均衡,
定理(策梅洛,1913):在有限广义完全信息博弈中,逆向归纳法的结果构成一个纯策略纳什均衡。此外,如果任何两个终端节点上的参与人的收益都不相同,则逆向归纳得出唯一的纳什均衡。
- 我们可以确定最下面的子博弈树的均衡,假设博弈到达这些节点时才会进行博弈;
- 玩家可以从游戏树的末端开始,并通过识别每个节点的最优行为来回溯树;
- 在双人零和博弈中,逆向归纳被称为Minimax算法;

举例: 蜈蚣博弈

两名玩家交替做出决定,每个回合在“停止”或“继续”之间做出选择,
- 这个游戏可以扩展到任何长;
- 收益以这样一种方式构建,即每个参与者总是选择“停止”是唯一的次博弈完美均衡;
这种次博弈完美均衡在直觉上并不吸引人,
- 球员似乎不太可能在比赛开始时选择S;
- 事实上,在实验室实验中,受试者一直选择C直到游戏接近尾声;
- 如果玩家连续玩几个回合,双方都将获得更高的收益;
➢信息集
- N:玩家集合;
- A:一组(单一)动作;
- H:一组(非终端)选择节;
- Z:终端节点集合;
- χ:一个动作函数,它分配给每个选择节点一组动作;
- ρ:一个参与者函数,它给每个选择节点分配一个参与者;
- σ:后继函数,将选择节点和动作映射到新的选择或终端节点;
- 𝑢=𝑢1,⋯,𝑢𝑛:一个效用函数,其中𝑢𝑖is为终端节点上的玩家i定义;

不完美信息的扩展型博弈

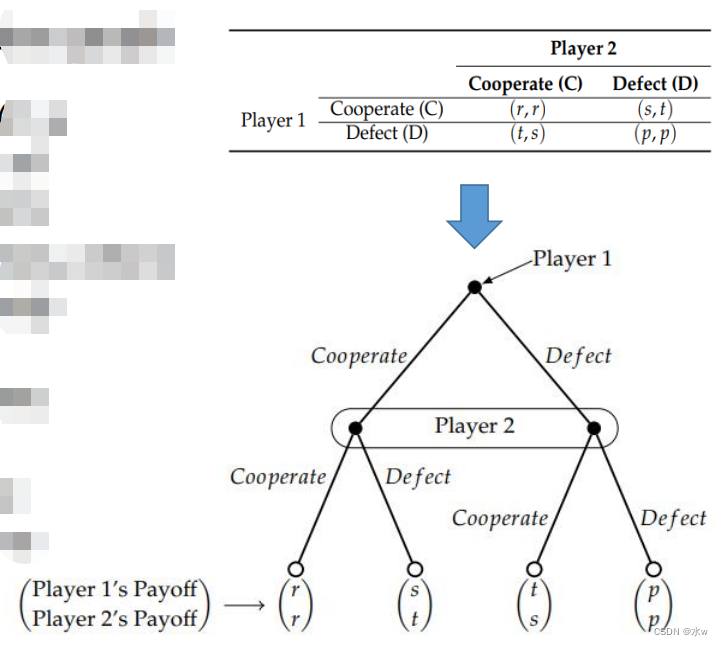
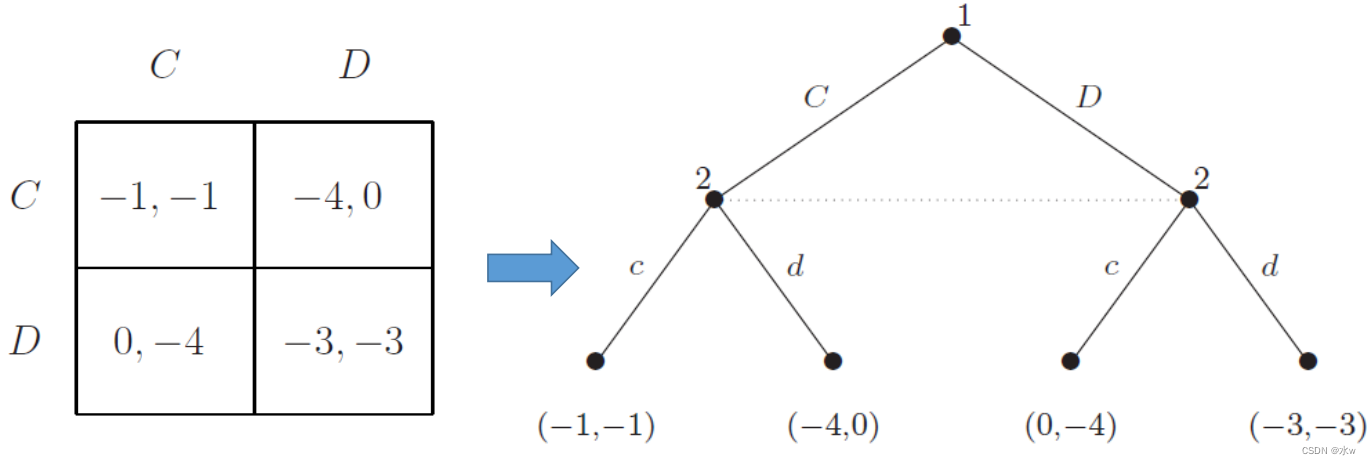
举例: 囚徒困境
任何正规形式的博弈都可以简单地转化为等价的不完全信息广义博弈
- 在囚徒困境博弈中,相当于让参与人1或2先选择
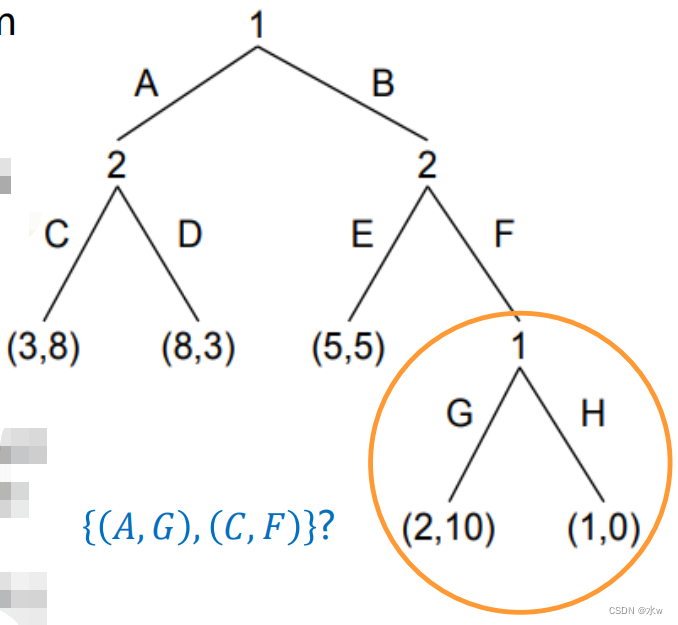
➢博弈纯策略
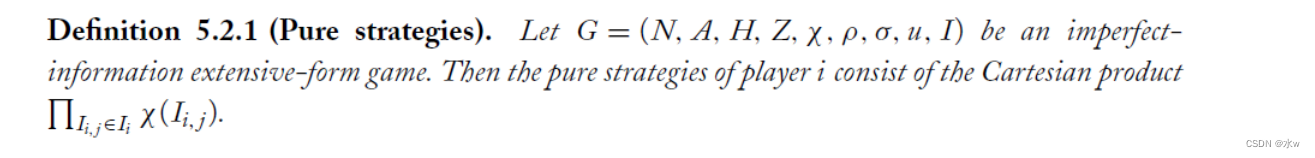
- 任何标准形式的游戏都可以被简单地转换成一个等价的不完美信息广泛形式的游戏;
- 囚徒困境是一种具有优势策略解的博弈,特别是具有纯策略纳什均衡的博弈,但对于一般的不完全信息博弈则不成立;
- 必须考虑混合策略来准确描述这种等价;
- 通过列举代理的纯策略,可以定义一个规范形式的博弈对应于任何给定的不完全信息广泛形式的博弈;
- 不完全信息博弈中的混合策略集可以简单地用标准形图中的混合策略集来定义;
- 纳什均衡集可以用相似的方法定义;
博弈混合策略与行为策略
行为策略不同于混合策略
- 混合策略在纯策略上分配概率分布。
- 例如,𝐴,𝐺概率为0.6𝐵,𝐻概率为0.4
- 行为策略在每个信息集合上对可能的行动集合分配一个概率分布。
- 例如,A的概率为0.5,B的概率为0.3,G的概率为0.3,H的概率为0.3
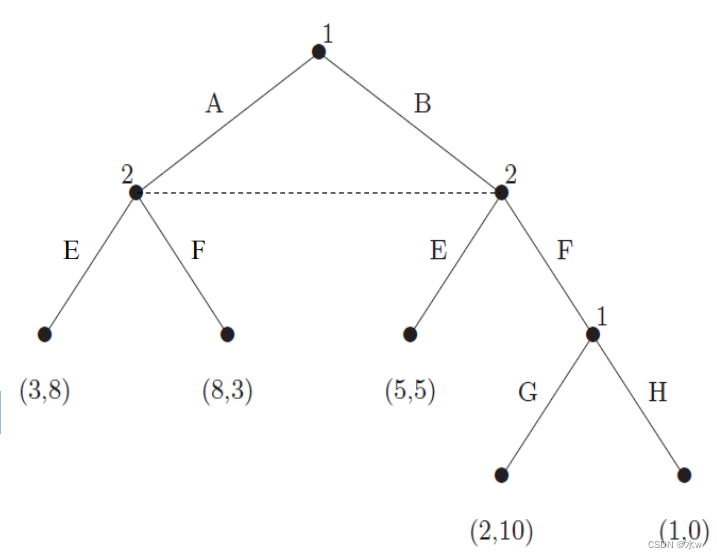
➢博弈混合策略
在不完全信息博弈中,混合策略和行为策略会产生不同的纳什均衡集。
- 在游戏中考虑混合策略
- 对于agent 1, R为严格优势策略;
- 对于agent 2, D为严格最佳对策;
- 因此,𝑅、𝐷是唯一的纳什均衡;
- 在混合策略中,agent 1概率决定采取L策略还是R策略(一)一旦决定,agent 1始终选择纯策略
- 拥有100,100的节点无关紧要,因为永远无法到达;
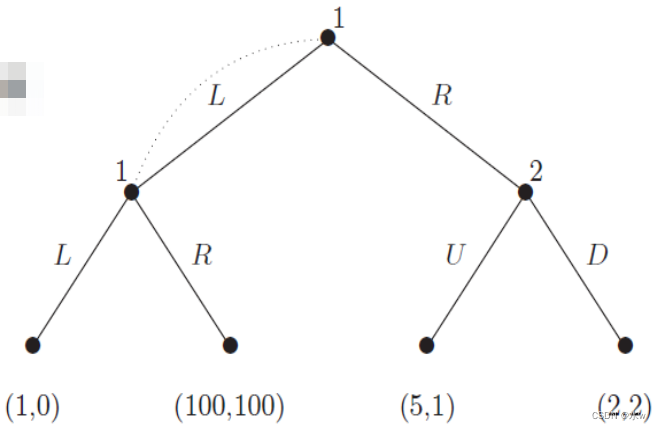
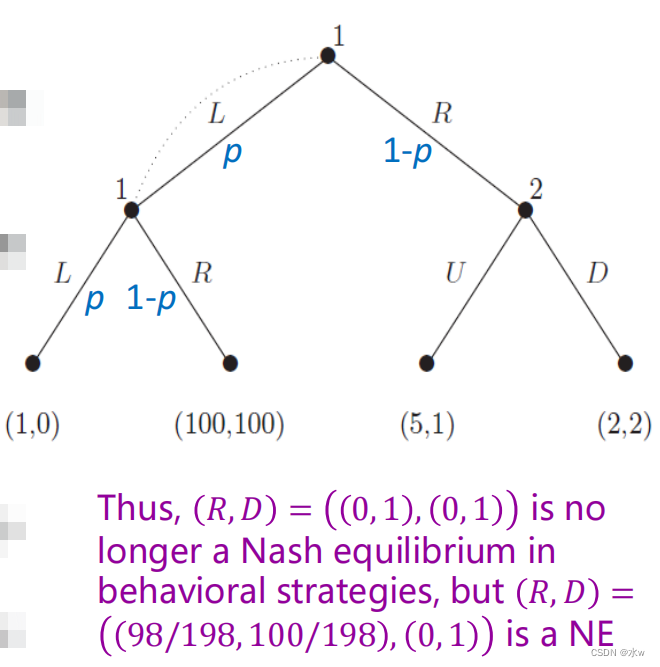
➢行为策略
在不完全信息博弈中,混合策略和行为策略会产生不同的纳什均衡集。
考虑游戏中的行为策略,
- Agent 1每次发现自己在信息集中时,可以重新随机化;
- 代理2 D是一个弱优势策略(独特的最好的回应所有的策略代理1除了L);
- 对于代理1,其最好的回应D𝑝,1−𝑝最大化其预期收益;
完美回忆博弈

(1)在完美回忆游戏中,每个玩家都记得自己过去知道什么,做过什么。
- 左:玩家1忘记了自己的动作
- 右:玩家1忘记了自己最后的动作是什么
每一个完美信息博弈都是一个完美回忆博弈。
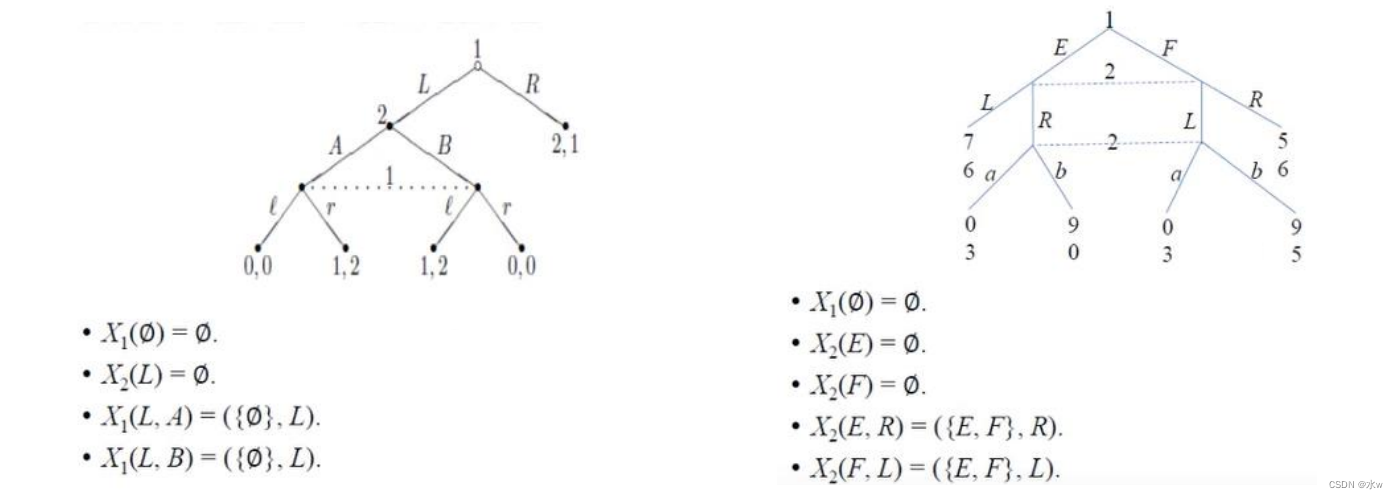
(2)在完全回忆的不完全信息博弈中,混合策略和行为策略是等价的。
- 但在一般不完全信息博弈中,混合策略和行为策略会产生不可比较的纳什均衡集
➢序贯均衡
纳什均衡对于完全信息博弈来说太弱了。
- 次博弈完美均衡不适用于不完全信息博弈
- 我们不再有明确定义的子游戏概念;
- 相反,我们在每个信息集中拥有的是一个“亚森林”或子博弈的集合;
- 处理这个问题的最著名的方法是序贯均衡
- 与“抖手完美”理念有共同之处;
- 但这个概念并没有提及游戏的树状结构;


























 1337
1337











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










