线性代数之 投影矩阵

上一篇讲了伪逆矩阵，本篇我们讲投影矩阵。

上一篇线性代数之 伪逆矩阵_水w的博客-CSDN博客

目录

二、投影矩阵

◼ 投影矩阵

◼ 举例

---

参考投影矩阵的奥秘_哔哩哔哩_bilibili

二、投影矩阵

投影矩阵是广泛应用于线性代数、矩阵计算、线性回归、奇异值分解中的一类幂等矩阵。投影矩阵广泛应用于线性代数中的矩阵运算，线性回归中以及qr分解，奇异值分解。

◼ 投影矩阵

在介绍投影矩阵之前，需要先引入一个概念：矩阵的值域

一个矩阵的所有列张成的线性空间就是A的值域。

在一个二维空间中，一条直线是由2个向量决定的。一个是其方向向量，另一个是其位置向量，或者说是法线向量。

那么这两个向量的无数线性组合，即两个向量构成的矩阵的值域，就张成了这样一个二维空间。如果只有直线的方向向量，就张成了二维向量的一维子空间，以为一维空间上是没有二维位置信息的，所有我们不关注法线向量。

现在我们在二维空间中，有一个点，想求助它在一维子空间中的投影。我们只需要求出点向量的模长以及它与一维子空间的夹角，再乘以一维子空间的单位方向向量，就可以得到投影向量在二维空间的表示了。

这里我们注意到点向量的模长乘以单位方向向量的模长，再乘以它们夹角的余弦值，这其实就是两个向量点积的定义。

至此，我们就得到了投影的向量求法。

到了三维空间中，两个不共线的三维向量就张成了一个二维子空间平面，我们想求出一个三维空间上的点，到这样一个二维空间上的投影，该怎么求？

在一个m维空间中，由n个线性无关的向量构成矩阵A张成了一个n维子空间平面，那么m维空间中的任意点想要投影到这样一个n维空间上，就需要通过一个投影矩阵P。

◼ 举例

例如，三维空间中，有两个线性无关的三维向量112和231，张成的一个2维子空间平面，那么投影到这个二维子空间平面上的投影矩阵就可以由公式求得。

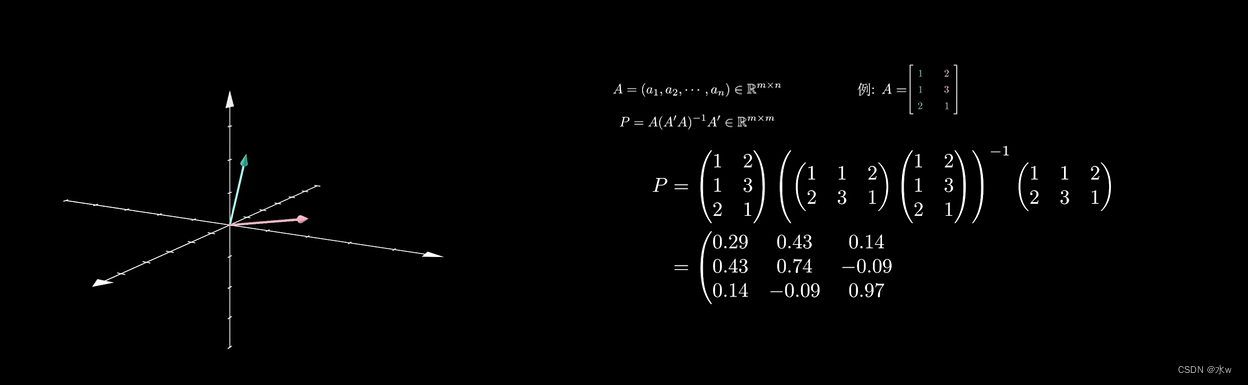
再将其乘以点向量就可以得到投影点的三维表示。

同理，二维空间的子空间是一条直线，我们只需要其方向向量来张成子空间直线，（这里将投影矩阵和向量求法进行了对比，利用看到两种方法的结果是一样的。）

 

问题：在n维空间中，如果有n个线性无关的向量张成的子空间的投影矩阵是什么样子的？

这里，分别对二维和三维进行了计算，可以看出它们的投影矩阵就是n维的单位矩阵。

这也很好理解，因为n维空间是由有n个线性无关的向量张成的，任何一点投影到自身所在的空间，必定还是自身。所以投影矩阵是单位矩阵，从而不改变其位置。