CapsNet 胶囊神经网络

论文参考： Dynamic Routing Between Capsules

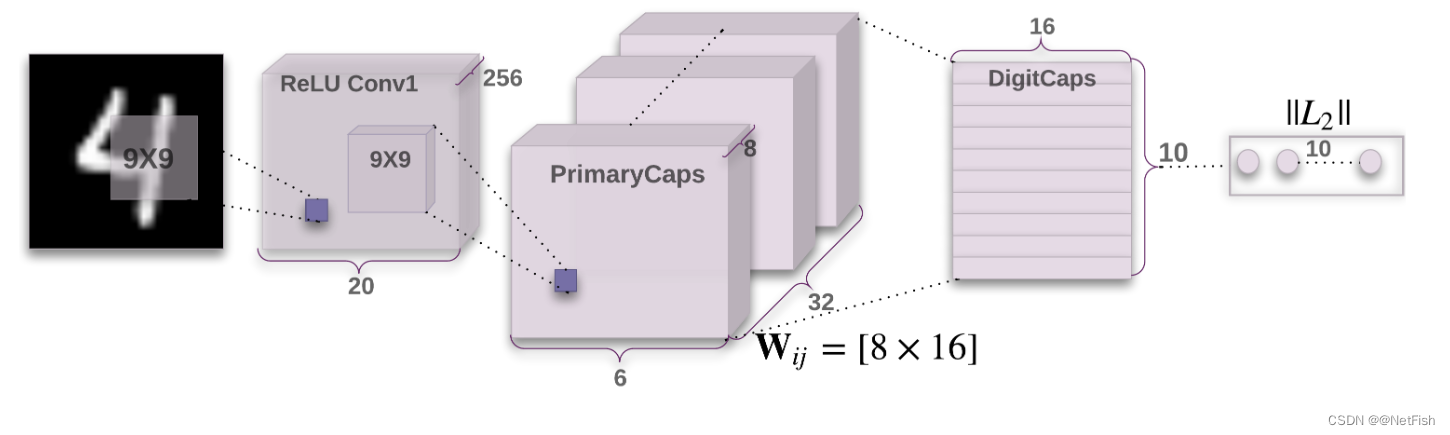
胶囊神经网络基本算法过程

网络输入图像尺寸为$28\times 28$，网络第一层为卷积层，卷积核大小为$9\times 9$，深度为1，步幅为1，个数为256(对应卷积后结果为256个通道)，卷积结果为$256\times 20\times 20$。网络第二层为Primary胶囊层，得到这一层本质上也是进行卷积操作，只是还要对卷积得到的256个通道按胶囊尺寸进行划分，从第一层到Primary胶囊层的卷积核大小为$9\times 9$，深度为256，步幅为2，个数为256，卷积结果为$256\times (6\times 6)$，然后在根据胶囊大小进行划分，8个通道的特征图为一组，一共32组，每一组有$6\times 6=36$个胶囊，共有$36\times 32=1152$个胶囊，每个胶囊由处于同一位置不同通道的8个神经元组成。胶囊其实就是一组数据(一组神经元)，构成一个向量，每个胶囊可能代表的是一个特征，向量的模长表示为原图存在该特征的概率，向量的方向表示该特征在原图的位姿信息。

从Primary层到Digit胶囊层，对于Digit层中第一个胶囊(向量)的计算，Primary层中的每个胶囊需要乘以权重W，并且再乘以系数c(c的值用一种叫动态路由的算法得到，每个胶囊的c值不共享)，然后将得到的值相加，再进行squashing操作(相当于一个非线性激活)，最终得到Digit层中的一个胶囊(向量)，每个胶囊的权重参数不共享，对于图中的网络而言，Digit层有十个胶囊，那么Primary层中的每个胶囊都有10个权重矩阵。Digit层中10个胶囊(向量)对应于预测的十个数字，向量的长度表示是该数字的概率，胶囊网络特有的损失函数叫Margin Loss，参数c由动态路由算法(Dynamic Routing)更新，权重W用经常使用的反向传播算法更新。

胶囊神经网络中具体算法细节

符号标记定义：Primary层用i标记，Digit层用j标记。$u_i$表示P层(Primary层)的第i个胶囊，$W_{ij}$表示P层中第i个胶囊到D层(Digit层)的第j个胶囊的权重系数，${\hat{\mathbf{u}}}_{j\mid i}$表示P层第i个胶囊到D层第j个胶囊时乘以权重之后的值， $c_{ij}$表示P层第i个胶囊到D层第j个胶囊时求和时的系数，$b_{ij}$是计算$c_{ij}$时的中间量，$s_j$表示P层所有胶囊乘以权重乘以系数相加求和后得到的未经squashing操作时得到的向量(此向量对应D层的第j个向量)，$v_j$表示最终得到的D层中的第j个向量(D层中每一层为一个胶囊向量)。

主要对Primary层到Digit层作算法说明，前面就是普通的卷积操作，所以不做赘述。

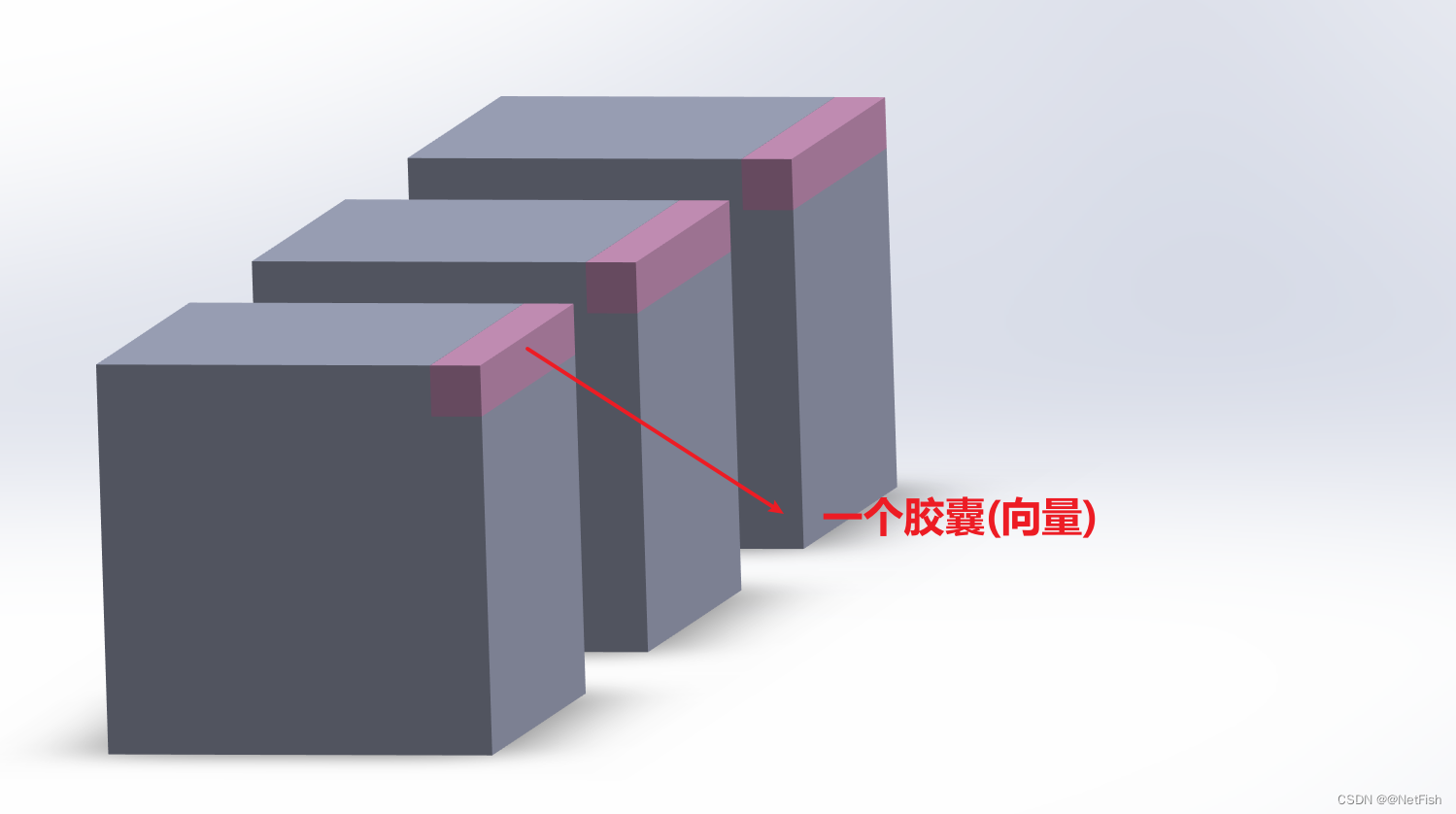
P层的得来其实就是对前面的卷积结果的256个通道进行重新划分，划分依据就是胶囊大小(论文中是1×8，其大小可以看为一个超参数)。划分完之后，$u_i$表示的一个胶囊(向量)如下图所示：

从P层到D层的第j个胶囊需要经过三个步骤：①P层所有胶囊$u_i$乘以各自的权重$W_{ij}$得到${\hat{\mathbf{u}}}_{j\mid i}$；②${\hat{\mathbf{u}}}_{j\mid i}$乘以各自的系数$c_{ij}$，并求和得到$s_j$；③对$s_j$进行squashing操作最终得到$v_j$。
$${\hat{\mathbf{u}}}_{j\mid i}={\mathbf{W}}_{ij}{\mathbf{u}}_i$$
$${\mathbf{s}}_j=\sum _i{c}_{ij}{\hat{\mathbf{u}}}_{j\mid i}$$
$${\mathbf{v}}_j=\frac{{\Vert {\mathbf{s}}_j\Vert }^2}{1+{\Vert {\mathbf{s}}_j\Vert }^2}\frac{{\mathbf{s}}_j}{\Vert {\mathbf{s}}_j\Vert }$$
其中$W_{ij}$为$m\times n$的矩阵，m对应P层胶囊向量的大小，n对应为D层胶囊的大小，因此论文中$m=8,n=16$，计算时所有权重均不共享；系数$c_{ij}$由动态路由算法得到，并且齐大小表示该胶囊向量进去下一层的概率，相当于对P层所有向量进入D层某个向量时做了挑选，跟D层的第j个向量相关的被保留其余的被过滤，这解释了为什么胶囊神经网络能不被噪音信息干扰；squashing操作则对原始向量$s_j$进行了一个缩放操作使齐介于0_{1之间，也相当于一个非线性激活；得到的$v_j$就表示了某一个数字的信息，其大小表示该数字存在的概率(因为其大小已经被映射到0}1了)。

系数$c_{ij}$的确定之动态路由算法

$b_{ij}$是计算$c_{ij}$时的中间量，迭代r次，这里$l$层指的是P层，$l+1$层指的使D层。算法示例是用P层所有的胶囊向量，计算D层中第j个向量时的过程(这里j可看作是一个固定值)。

首先初始化$b_{ij}$都为0，然后进行r次迭代更新。用$softmax(b_i)$得到$c_i$(这里脚标没有j是因为j在这里是固定值)，使用softmax操作保证所有$c_i$之和为1，那么$c_i$就可代表为P层中第i个向量进入下一层时的概率，将对D层第j个向量有用的向量挑选出来，并非将P层所有向量都送入下一层。
$$c_{ij}=\frac{\exp \left(b_{ij}\right)}{{\sum }_k\exp \left(b_{ik}\right)}$$
更新操作$b_{ij}\leftarrow b_{ij}+{\hat{\mathbf{u}}}_{j\mid i}\cdot {\mathbf{v}}_j$中向量乘法${\hat{\mathbf{u}}}_{j\mid i}\cdot {\mathbf{v}}_j=\Vert {\hat{\mathbf{u}}}_{j\mid i}\Vert \cdot \Vert {\mathbf{v}}_j\Vert \cdot \cos \theta$ 可理解为与最终的和向量$v_j$越接近的${\hat{\mathbf{u}}}_{j\mid i}$(大小、方向)，其乘积后的值也就越大(反之就越小)，那么下次迭代时$b_{ij}$越大，相应$c_i$也就越大，那么其进入下一层的概率也就越大，也就是说$u_i$这个向量被挑选出来。根据此规则在训练一个epoch时迭代r次更新$c_i$。

$W_{ij}$训练时的损失函数之Margin Loss

边界损失函数：设有一个阈值，超过阈值有损失，低于阈值无损失(或相反)
$$L_k=T_k\max {\left(0,m^{+}-\Vert {\mathbf{v}}_k\Vert \right)}^2+\lambda \left(1-T_k\right)\max {\left(0,\Vert {\mathbf{v}}_k\Vert -m^{-}\right)}^2$$
$L_k$表示D层第k个向量的损失，$T_k$为当前D层中第k个向量对应的标签(比如输入图片为4时，那么D层第5个胶囊的标签为1，其余为0)；$\lambda$为计算系数(超参数)；$m^{+}$和$m^{-}$为设置的阈值(超参数)，文中$m^{+}=0.9,m^{-}=0.1$；设输入图片为4，$k=5$时，那么$T_k=1$，按照公式后半部分为0，只剩$L_k=\max {\left(0,m^{+}-\Vert {\mathbf{v}}_k\Vert \right)}^2$，当$\Vert {\mathbf{v}}_k\Vert >0.9$时，则$L_k=0$，不计算损失，当$\Vert {\mathbf{v}}_k\Vert <0.9$时，$L_k>0$，计算损失，意义为：使D层预测对应数字的向量模长大于0.9；当$k\ne 5$时，那么$T_k=0$，按照公式前半部分为0，只剩$L_k=\lambda \left(1-T_k\right)\max {\left(0,\Vert {\mathbf{v}}_k\Vert -m^{-}\right)}^2$，当$\Vert {\mathbf{v}}_k\Vert >0.1$时，则$L_k>0$，计算损失，当$\Vert {\mathbf{v}}_k\Vert <0.1$时，$L_k=0$，不计算损失，意义为：使D层与预测数字不对应的向量的模长小于0.1；经过迭代后，输入数字时，D层与其对应的向量的模长大于0.9(即概率大于0.9)，于其不对应的向量的模长小于0.1(概率小于0.1)，从而可以正确识别输入数字。