【阅读文献笔记】Mamba: Linear-Time Sequence Modeling with Selective State Spaces

Mamba模型的提出者为Albert Gu、Tri Dao，前者现在是CMU助理教授，多年来一直推动SSM发展，曾在DeepMind 工作，后者则为Flash Attention一作。

Mamba模型作为Transformer极具革命性的平替，开拓了AI界研究大模型的思路，讲清三个问题：

Ø 1.注意力机制的局限和Transformer的硬伤

Ø 2.状态空间模型SSM

Ø 3.Mamba的三大创新

从SSM、HiPPO、S4起步，逐步推导到Mamba

Transformer的死穴

Transformer 结构的核心是自注意力机制层，不管Encoder，还是Decoder，序列数据都先经过位置编码后喂给这个模块。

这里有个天然的缺陷，就是自注意力机制的计算范围仅限于窗口内，而无法直接处理窗口外的元素。这种机制无法建模超出有限窗口的任何内容，看不到更长序列的世界。

Transformer模型的二次复杂度问题

于是有人说了，那增加窗口长度不就行了，理论上可行。但，这样会导致计算复杂度随着窗口长度的增加呈平方增长O(n2)，因为每个位置的计算都需要与窗口内的所有其他位置进行比较，如右图所示。

推理的缺陷

在生成序列中的下一个tokens时，我们必须重新计算整个序列的注意力，即使某些tokens已经被生成。

为长度为L的序列生成tokens大约需要L²计算，如果序列长度增加，计算成本可能会很高。

Transformer忽视了数据内在结构的细腻关联关系，而是采取了一种一视同仁的暴力关联模式，好处是直接简单，但显然参数效率低下，冗余度高，训练起来不易。

让长序列数据建模回归传统，某种程度上说，这是整个SSM类模型思考问题的初衷和视角。而Mamba是其中的佼佼者。

状态空间模型 (SSM)

状态空间模型（SSM），与Transformer和RNN一样，用于处理信息序列，例如文本和信号。在本节中，我们将探讨SSM的基本概念以及它们如何与文本数据相互作用。

什么是状态空间？

状态空间是一组能够完整捕捉系统行为的最少变量集合。它是一种数学建模方法，通过定义系统的所有可能状态来表述问题。

想象我们正在走过一个迷宫。这里的“状态空间”就像是迷宫中所有可能位置的集合，即一张地图。地图上的每个点都代表迷宫中的一个特定位置，并包含了该位置的详细信息，比如离出口有多远

虽然状态空间模型利用方程和矩阵来记录这种行为，但它们本质上是一种记录当前位置、可能的前进方向以及如何实现这些移动的方法。

描述状态的变量（在我们的迷宫例子中，这些变量可能是X和Y坐标以及与出口的相对距离）被称作“状态向量”。

这个概念听起来是不是有些耳熟？那是因为在语言模型中，我们经常使用嵌入或向量来描述输入序列的“状态”。

在神经网络的语境中，“状态”通常指的是网络的隐藏状态。在大型语言模型的背景下，隐藏状态是生成新tokens的一个关键要素。

什么是状态空间模型？

状态空间模型（SSM）是用来描述这些状态表示，并根据给定的输入预测下一个可能状态的模型。

SSM是控制理论中常用的模型，在卡尔曼滤波、隐马尔可夫模型都有应用。它是利用了一个中间的状态变量，使得其他变量都与状态变量和输入线性相关，极大的简化问题。

物理例子推导公式

当我们给定一个力u(t) 作为系统的输入，求物体M的位移y(t) 作为系统的输出。

根据受力平衡可以得到表达式

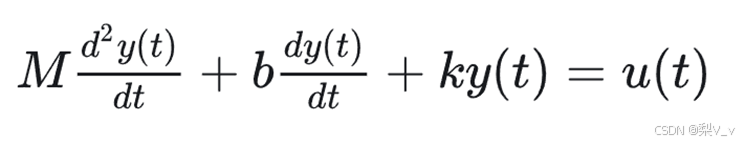
上式是一个典型的二阶微分方程，但是对于任意的时间序列来说没有解析解，如何得到逼近的解是关键。

如果我们构建一个状态向量

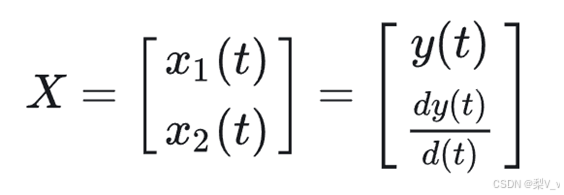
这里直接将输出函数和输出的函数的一阶导数作为状态向量。其实定义是多样的，只要能简化计算过程即可。于是可以得到

即

同时，输出y也可以写成关于当前状态的方程：

因此，当给定输入u(t) ,并给定一个初始状态x(0) 时，就可以实时的计算输出。

一般来说，可以得到如下两个方程

即模型的输出量，以及状态的变换量都可以由当前状态和输入量计算出来。下图也表明了这个过程。

状态空间模型（SSM）

状态空间模型（SSM）假定动态系统（比如在三维空间中移动的物体）的状态可以通过两个数学方程来预测，这两个方程描述了系统在时间t时的状态如何随时间演变。

这两个方程构成了状态空间模型的核心。

状态方程展示了输入如何通过矩阵B影响状态，以及状态如何通过矩阵A随时间变化。

正如我们之前看到的，h(t)指的是任何给定时间t的潜在状态表示，而x(t)指的是某个输入。

输出方程描述了状态如何转换为输出（通过矩阵 C）以及输入如何影响输出（通过矩阵 D ）。

注意：矩阵A、B 、C和D通常也称为参数，因为它们是可学习的。

设想我们有一个输入信号x(t)，这个信号首先与矩阵B相乘，而矩阵B刻画了输入对系统的影响程度。

 

更新后的状态（类似于神经网络的隐藏状态）是一个潜在空间，它包含了环境的核心“知识”。我们将这个状态与矩阵A相乘，矩阵A揭示了所有内部状态是如何相互连接的，因为它们代表了系统的基本动态。

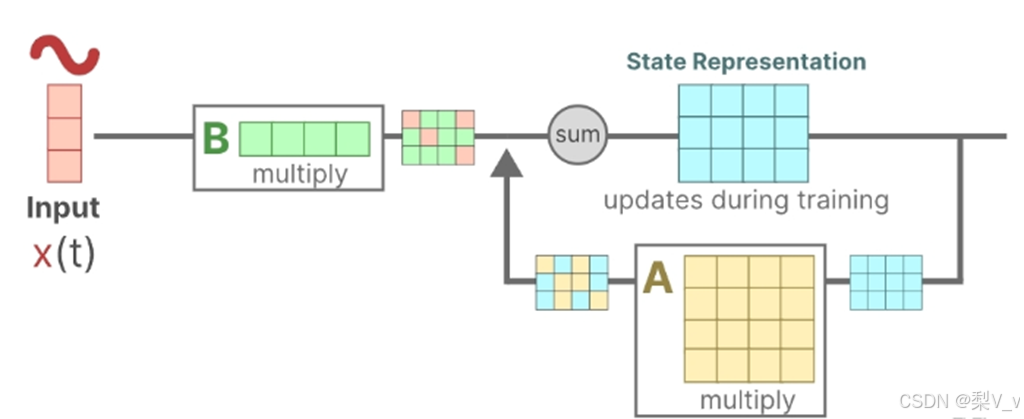
矩阵A在创建状态表示之前被应用，并在状态表示更新之后进行更新。

利用矩阵C来定义状态如何转换为输出。

最后，我们可以利用矩阵 D提供从输入到输出的直接信号。这通常也称为跳跃连接。

由于矩阵 D类似于跳跃连接，因此在没有跳跃连接的情况下，SSM 通常被视为如下。

时不变特性

之所以叫时不变（与时间无关），就是 ABCD参数是固定的，这当然是一种假设，而且是个强假设。D在许多实际系统中，它可以是零。很多人学 SSM渐渐就忘了这个强假设。Transformer本身是没有这样的假设的，也就是说可以用于时变系统和非线性系统。

牺牲通用性，换来特定场景下的更高性能，这就是所有SSM模型的最底层逻辑。

连续系统转化为离散系统

采用了零阶保持（Zero-Order Hold）技术。其工作原理如下：每当接收到一个离散信号时，我们就保持该信号值不变，直到下一个离散信号的到来。

我们保持信号值的时间由一个新的可学习参数表示，这个参数称为步长Δ 。它代表了输入信号的分辨率。（效果上看，左图代替右图。）

离散化

离散化主要是为了方便计算机处理。

从数学角度来看，我们可以按照以下方式应用零阶保持技术：

有几种有效的离散化方法，如欧拉方法、零阶保持器(Zero-order Hold, ZOH)方法或双线性方法。欧拉方法是最弱的，但在后两种方法之间的选择是微妙的。事实上，S4论文采用的是双线性方法，但Mamba使用的是ZOH。

我们从一个连续的SSM（函数到函数，x(t)→y(t)）到一个离散SSM（序列到序列，xₖ→yₖ）。

这里，矩阵A和B现在表示模型的离散参数。

我们使用k而不是t来表示离散时间步长，并在我们提到连续 SSM 与离散 SSM 时使其更加清晰。

矩阵A的重要性

矩阵A可以说是状态空间模型（SSM）公式中最为关键的组成部分之一。正如我们之前在循环表示中所讨论的，矩阵A负责捕捉先前状态的信息，并利用这些信息来构建新的状态。

如何创建一个能够保持大容量记忆（即上下文大小）的矩阵A呢？

HiPPO

HiPPO（Hungering Hungry Hippo）​​​​，这是一个高阶多项式投影运算器。HiPPO的目标是将迄今为止观察到的所有输入信号压缩成一个系数向量。

HiPPO利用矩阵A构建一个状态表示，这个表示能够有效地捕捉最近token的信息，并同时让旧token的影响逐渐减弱。其公式可以表示为：

实践证明，使用HiPPO构建矩阵A的方法明显优于随机初始化。因此，它能够更精确地重建最新的信号（即最近的tokens），而不仅仅是初始状态。

HiPPO矩阵的核心在于其能够生成一个隐藏状态，用以存储历史信息。

（在数学上，这是通过追踪勒让德多项式的系数来实现的，这使得它能够近似所有历史数据。）

S4

HiPPO随后被应用到循环和卷积表示中，以处理远程依赖关系。这导致了序列的结构化状态空间Structured State Space for Sequences（S4）的产生，这是一种能够有效处理长序列的SSM。

S4由三部分组成：

Ø 状态空间模型

Ø HiPPO用于处理远程依赖关系

Ø 用于创建循环和卷积表示的离散化处理

这种类型的SSM具有多个优点，具体取决于您选择的表示形式（无论是循环还是卷积）。它还能够通过构建HiPPO矩阵来有效地处理长文本序列，并高效地存储记忆。

Mamba的三大创新

Mamba = 有选择处理信息 + 硬件感知算法 + 更简单的SSM架构

Ø 对输入信息有选择性处理(Selection Mechanism)

Ø 硬件感知的算法(Hardware-aware Algorithm)

Ø 更简单的架构

1.简单的选择机制

通过“参数化SSM的输入”，让模型对信息有选择性处理，以便关注或忽略特定的输入

这样一来，模型能够过滤掉与问题无关的信息，并且可以长期记住与问题相关的信息

好比，Mamba每次参考前面所有内容的一个概括，越往后写对前面内容概括得越狠，丢掉细节、保留大意

各个模型的核心特点

模型	对信息的压缩程度	训练的效率	推理的效率
Transformer(注意力机制)	Transformer对每个历史记录都不压缩	训练消耗算力大	推理消耗算力大
RNN	随着时间的推移，RNN 往往会忘记某一部分信息	RNN没法并行训练	推理时只看一个时间步 故推理高效(相当于推理快但训练慢)
CNN		训练效率高，可并行「因为能够绕过状态计算，并实现仅包含(B, L, D)的卷积核」
SSM	SSM压缩每一个历史记录		矩阵不因输入不同而不同，无法针对输入做针对性推理
Mamba	选择性的关注必须关注的、过滤掉可以忽略的	Mamba每次参考前面所有内容的一个概括，兼备训练、推理的效率

有选择地保留信息

SSM的循环表示创建了一个非常高效的小状态，因为它压缩了整个历史记录。然而，与不压缩历史记录（通过注意力矩阵）的Transformer模型相比，它的功能要弱得多。

Mamba的目标是实现两全其美：创建一个像Transformer一样强大的小状态。

Mamba通过有选择地将数据压缩到状态中来实现这一目标。当输入一个句子时，通常会包含一些没有多大意义的信息，例如停用词。

为了有选择地压缩信息，我们需要参数依赖于输入。为此，我们首先探讨训练期间SSM中输入和输出的维度。

S4中三个矩阵：A∈RN×N,B∈RN×1,C∈R1×N矩阵都可以由𝑁个数字表示。

但为了对批量大小为B，长度为L，具有D个通道的输入序列𝑥进行操作。总之，类似总计有B个序列，每个序列的长度为L，且每个序列中每个token的维度为D。

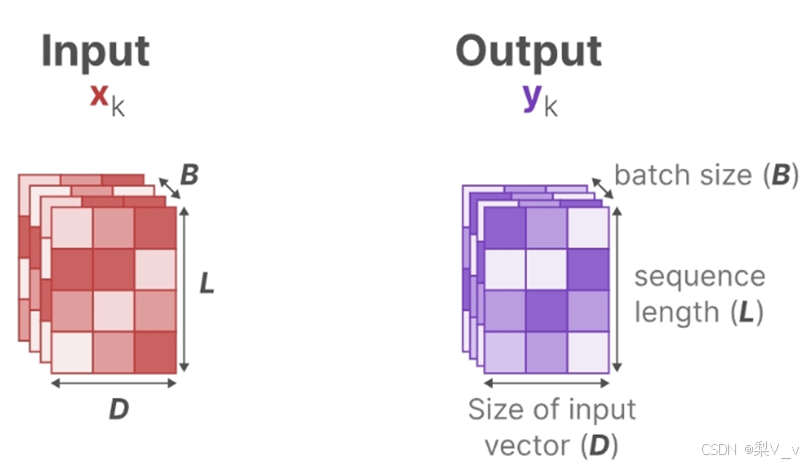
在结构化状态空间模型 (S4) 中，矩阵A、B和C独立于输入，因为它们的维度N和D是静态的并且不会改变。

将几个参数 ∆，B，C 设置为输入函数，并在整个过程中改变张量形状。这些参数现在都有一个长度维度 L ，意味着模型已经从时间不变变为时间可变。

 Mamba：从S4到S6的算法变化流程

从S4到S6的过程中 影响输入的𝐵矩阵、影响状态的𝐶矩阵的大小从原来的(D,N)变成了(B,L,N)

这三个参数分别对应batch size、sequence length、hidden state size

且Δ的大小由原来的D变成了(B,L,D)，意味着对于一个 batch 里的每个 token (总共有 BxL 个)都有一个独特的Δ

  Mamba通过合并输入的序列长度和批量大小，使得矩阵B和C以及步长Δ都取决于输入。

  这意味着对于每个输入标记，我们现在有不同的B和C矩阵，可以解决内容感知问题！

虽然𝐴没有变成data dependent，但是通过SSM的离散化操作之后，(𝑨,𝑩)    (¯A,¯B)    会经过outer product变成(B, L, N, D)的data dependent张量，算是以一种parameter efficient的方式来达到data dependent的目的 

简言之，A离散化之后 𝑨¯A=exp(ΔA) , Δ 的“输入数据依赖性”能够让整体的 𝑨¯A 与输入相关

2.硬件感知的设计

  并行扫描(parallel scan)且借鉴Flash Attention

 如之前所述，由于A B C这些矩阵现在是动态的了，因此无法使用卷积表示来计算它们(CNN需要固定的内核)，因此，我们只能使用循环表示，如此也就而失去了卷积提供的并行训练能力

扫描操作

Mamba通过并行扫描(parallel scan)算法使得最终并行化成为可能，其假设我们执行操作的顺序与关联属性无关

因此，我们可以分段计算序列并迭代地组合它们，即动态矩阵B和C以及并行扫描算法一起创建选择性扫描算法(selective scan algorithm)

在并行计算中，时间复杂度 O(n/t) 中的 t ，通常代表用于执行任务的处理器或计算单元的数量

核融合

最新 GPU 的一个缺点是其小型但高效的 SRAM 与大型但效率稍低的 DRAM 之间的传输 (IO) 速度有限。在 SRAM 和 DRAM 之间频繁复制信息成为瓶颈。

Flash Attention技术

利用内存的不同层级结构处理SSM的状态，减少高带宽但慢速的HBM内存反复读写这个瓶颈

具体而言，就是限制需要从 DRAM 到 SRAM 的次数(通过内核融合kernel fusion来实现)，避免一有个结果便从SRAM写入到DRAM，而是待SRAM中有一批结果再集中写入DRAM中，从而降低来回读写的次数

3.The Mamba Block

将大多数SSM架构比如H3的基础块，与现代神经网络比Transformer中普遍存在的门控MLP相结合，组成新的Mamba块，重复这个块，与归一化和残差连接结合，便构成了Mamba架构

为何要做线性投影?

经过线性投影后，输入嵌入的维度可能会增加，以便让模型能够处理更高维度的特征空间，从而捕获更细致、更复杂的特征

为什么SSM前面有个卷积？

SSM之前的CNN负责提取局部特征(因其擅长捕捉局部的短距离特征)，而SSM则负责处理这些特征并捕捉序列数据中的长期依赖关系，两者算互为补充

Ø 直接将SSM参数(Δ,A,B,C)从慢速HBM加载到快速SRAM中

Ø 注意，当输入从HBM加载到SRAM时，中间状态不被保存，而是在反向传播中重新计算

Ø 然后，在SRAM中进行离散化，得到(B,L,D,N)的 𝑨 , 𝑩 ¯ A, ¯ B

Ø 接着，在SRAM中进行scan得到(B,L,D,N)的输出

Ø 最后，multiply and sum with C，得到(B,L,D)的最终输出写回HBM

02.mamba的应用实例与一般性的实验结果

通过mamba预测下一个token的示例

首先进行线性投影以扩展输入嵌入，然后，在应用选择性 SSM之前先进行卷积

最后，包含归一化层和用于选择“预测的token”的softmax

其中的“选择性SSM(即Selective SSM)”具有以下属性：

ØRecurrent SSM通过离散化创建循环SSM

ØHiPPO对矩阵A进行初始化A以捕获长程依赖性

Ø选择性扫描算法(Selective scan algorithm)选择性压缩信息

Ø 硬件感知算法(Hardware-aware algorithm)加速计算

三个任务的对比：coping、selective copying、induction heads

Ø 复制任务的标准版本涉及输入和输出元素之间的固定间距，可以通过线性递归和全局卷积等时不变模型轻松解决

Ø 选择性复制任务在输入之间具有随机间距，需要使用时变模型，在内容上能够灵活地选择记忆或忽略输入

Ø 归纳头部任务是联想回忆的一个例子，需要根据上下文检索答案，这是LLM关键的能力

实验结果

Ø Mamba在Chinchilla缩放定律下预训练时，语言任务优于同类开源模型

Ø 下游任务上，每个规模尺寸的Mamba都是同类最佳，并且通常与两倍规模的基线性能匹配，特别是当序列长度增加到512k时，相比使用FlashAttention-2的Transformer快几个数量级，而且不会内存不足

03     Mamba模型的应用潜力

几种具有代表性的视觉 Mamba 主干网络，以阐明将 Mamba 应用于 CV 的基本原理和创新。

Pure Mamba

Vim:

是一种基于Mamba的架构，直接在图像块序列上操作，类似于Vision Transformer（ViT）。输入图像首先被转换为展平的2D块，然后通过线性投影层进行向量化，并添加位置嵌入以保留空间信息。Vim块是一个Mamba块，它集成了一个向后的SSM路径以及向前的一个。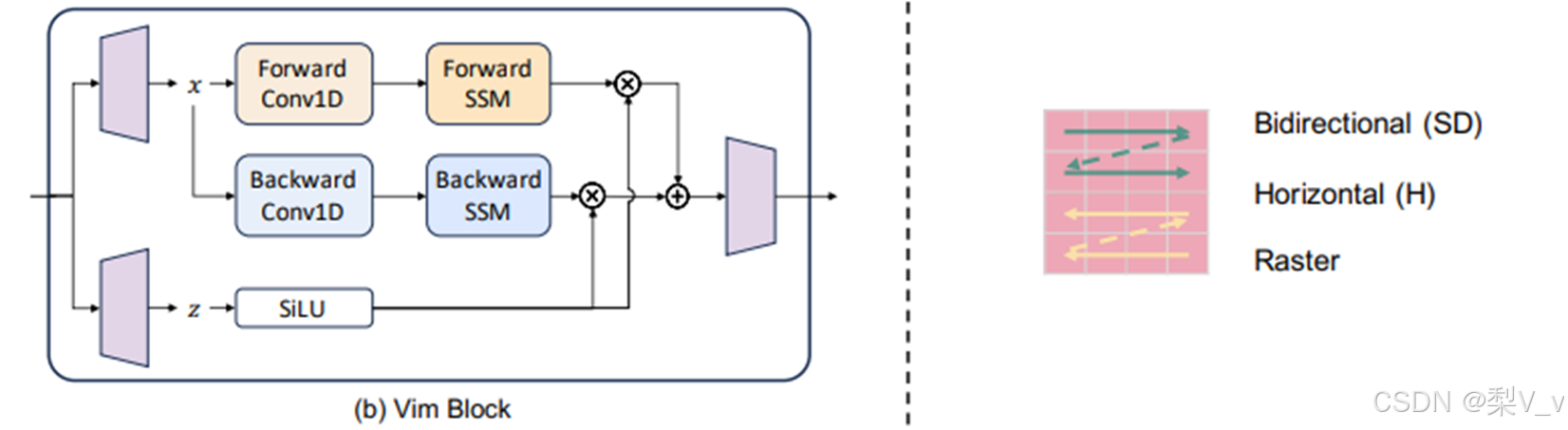

VMamba:

VMamba用于解决将Mamba应用于2D图像时遇到的两个挑战：由Mamba选择机制的1D和因果属性引起的问题。VMamba引入了一个CrossScan Module (CSM)，使用双向扫描模式和水平及垂直扫描轴。该模块将输入图像沿水平和垂直轴转换为块序列，并沿四个方向扫描这些序列。

Mamba-ND

Mamba-ND:

Mamba-ND旨在将Mamba扩展到包括图像和视频在内的多维数据。它将1D Mamba层视为一个黑盒，并探索如何解开和排序多维数据。Mamba-ND主要解决数据缺乏预定义排序同时具有固有空间维度的挑战。

PlainMamba

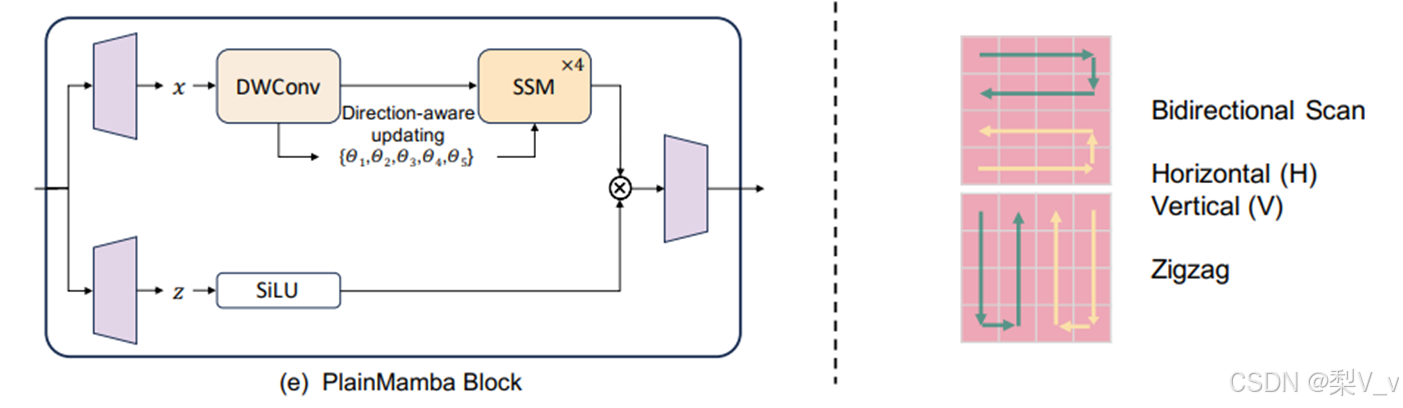
PlainMamba:

PlainMamba被设计为一个非层次化的架构，以满足多个目标，例如促进多级特征融合、有效融合多模态数据、提供更好的泛化能力，以及优化硬件加速。PlainMamba块类似于Mamba块，但是使用了2D深度卷积层来替代1D卷积层，并且调整了选择性扫描机制以适应2D图像。

Hybrid Mamba

LocalMamba:

LocalMamba解决了Vim和VMamba模型中观察到的一个重大限制，即在单一扫描过程中空间局部性令牌之间的依赖关系被破坏。LocalMamba将输入图像划分为多个局部窗口，并在不同的方向上执行SSM，同时保持全局SSM操作。

EfficientVMamba:

EfficientVMamba引入了高效的2D扫描（ES2D）技术，该技术使用特征图上的块的空洞采样来减少计算负担。ES2D用于提取全局特征，同时并行的卷积分支用于提取局部特征。

Mamba作为一种新型的长序列建模架构，在多个计算机视觉领域展现出了卓越的性能和高效的计算实现。

Mamba模型总结

Ø 主要解决 Transformer 模型的二次复杂度问题。

Ø 优势在于长序列任务上的优异性能与较低的计算复杂度。

Ø 分析 Mamba 模型在结构上与 Transformer 的不同之处。

Ø Mamba 模型 具有的应用潜力。