基于 ACF 与 PACF 的洪水预测分析：方法、应用及代码示例

最新推荐文章于 2025-05-24 10:42:46 发布

梨V_v

最新推荐文章于 2025-05-24 10:42:46 发布

阅读量685

点赞数 13

文章标签： python numpy 开发语言

本文链接：https://blog.csdn.net/qq_46460379/article/details/148168911

版权

一、引言

洪水是一种常见的自然灾害，对人民的生命财产安全和社会经济发展构成严重威胁。准确预测洪水的发生及发展对于防洪减灾工作至关重要。时间序列分析在洪水预测领域有着广泛应用，其中自相关函数（ACF）和偏自相关函数（PACF）是两种重要的分析工具，能够帮助我们深入理解洪水数据的内在规律，为预测模型的建立提供有力依据。

ACF描述了一个观测值与另一个观测值之间的自相关，包括直接和间接的相关性信息。这意味着我们可以预期AR(k)时间序列的ACF使用了k的滞后，并且这种关系的惯性将继续影响到之后的滞后值，并随着逐步削弱到在某个点上缩小到没有。
PACF只描述观测值与其滞后(lag)之间的直接关系。这表明，超过k的滞后值(lag value)不会再有相关性。

截尾：时间序列的自相关函数（ACF）或偏自相关函数（PACF）在某阶后均为0的性质（比如AR的PACF）
- 在大于某个常数k后快速趋于0为k阶截尾
拖尾：ACF或PACF并不在某阶后均为0的性质（比如AR的ACF）
- 始终有非零取值，不会在k大于某个常数后就恒等于零(或在0附近随机波动)
AR模型： PACF截尾，ACF拖尾。
MA模型： ACF截尾，PACF拖尾。
ARMA模型： ACF和PACF均拖尾。
没有合适模型：ACF和PACF均截尾。

二、ACF 自相关法

（一）基本原理

ACF（Autocorrelation Function）用于衡量时间序列中不同时刻数据之间的相关性。对于洪水时间序列，其自相关系数反映了不同时滞下洪水数据的相关程度。计算公式为：

其中，xt 表示洪水时间序列在时刻 t 的数据，xˉ 是序列的均值，k 为滞后阶数。

（二）性质及应用

性质：ACF 图横坐标表示滞后的阶数，纵坐标表示对应的滞后序列与原始序列的相关系数。随着滞后阶数增加，相关性逐渐降低。图中蓝色区域为置信区间，若相关系数落在置信区间内，表明对应序列相关性不显著。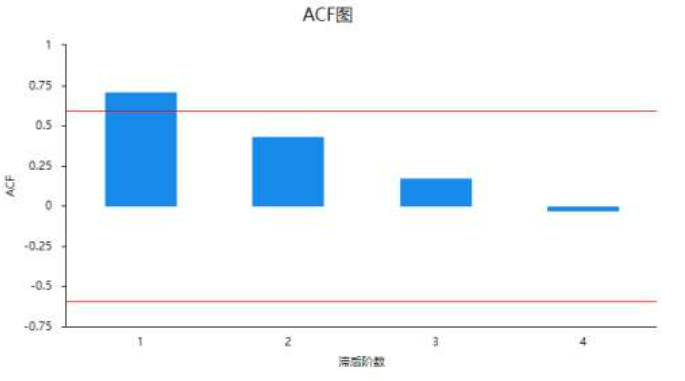

从自相关ACF图可知，可以理解其为4阶截尾，也或者理解为拖尾现象，但一般情况下4阶会比较大，因而暂认为当前数据为拖尾现象。
应用：通过 ACF 图可以初步判断洪水时间序列的平稳性和季节性等特征。若序列平稳，ACF 图会呈现出指数衰减或正弦衰减等规律；若存在季节性，会在特定滞后阶数上出现显著峰值。

（三）代码示例

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf

# 假设 flood_data 为洪水时间序列数据
flood_data = pd.read_excel('flood_data.xlsx', engine='openpyxl')
flood_data['flood'].plot()
plot_acf(flood_data['flood'], lags=40, adjusted=False)
plt.show()

三、PACF 偏自相关法

（一）基本原理

PACF（Partial Autocorrelation Function）用于衡量时间序列中两个时间点数据之间的直接相关性，排除中间时间点的影响。对于洪水时间序列，其偏自相关系数表示在控制了中间滞后项的影响后，当前洪水数据与滞后 k 期洪水数据之间的直接相关性。计算公式较为复杂，通常借助统计软件或编程库进行计算。

（二）性质及应用

性质：PACF 图同样以滞后的阶数为横坐标，相关系数为纵坐标。与 ACF 图不同的是，PACF 图更侧重于反映序列之间的直接相关性。

从偏自相关图PACF可以看出：从2阶开始快速趋近于0，意味着在2阶截尾（也可以看成是3阶截尾，或者4阶截尾均可）。结合判断标准可知：自相关图为拖尾，偏自相关图为2阶截尾。因此最终模型选择为AR(2)较为适合。
应用：在洪水预测中，PACF 图可用于确定自回归模型的阶数。当 PACF 图在某个滞后阶数之后突然截断，即相关系数迅速变为零或落在置信区间内时，该滞后阶数可作为自回归模型的阶数选择依据。

SPSS在线_SPSSAU_自相关acf/偏自相关pacf图分析

（三）代码示例

from statsmodels.graphics.tsaplots import plot_pacf

plot_pacf(flood_data['flood'], lags=40, method='ols')
plt.show()

四、ACF 与 PACF 在洪水预测中的联合应用

（一）模型识别

在建立洪水预测模型时，首先利用 ACF 和 PACF 图对洪水时间序列的性质进行分析。若 ACF 图呈现拖尾特征，而 PACF 图在滞后 p 阶截尾，则可考虑建立 AR（p）模型；若 ACF 图在滞后 q 阶截尾，PACF 图呈现拖尾特征，则适合建立 MA（q）模型；若两者均呈现拖尾特征，则可尝试建立 ARMA 或 ARIMA 模型。关于上述ACF和PACF图的解读上，通常需要结合研究人员的主观判断加以定夺（并且很多时候可以有多个候选模型），没有绝对的标准。

（二）参数估计与模型验证

根据 ACF 和 PACF 的分析结果初步确定模型阶数后，使用历史洪水数据对模型参数进行估计。然后通过计算模型残差的 ACF 和 PACF，检查残差是否为白噪声序列，以验证模型的合理性。若残差序列的 ACF 和 PACF 均无显著相关性，则说明模型对洪水数据的拟合效果较好，可以用于洪水预测。

（三）实际案例分析

假设我们有一组某地区过去多年的月度洪水数据，通过绘制 ACF 和 PACF 图发现，ACF 图在滞后 1、2 阶有显著峰值，之后逐渐衰减；PACF 图在滞后 1 阶有显著峰值，滞后 2 阶之后截尾。根据这些特征，我们初步确定建立 AR（1）模型。利用历史数据估计模型参数后，对模型进行验证，发现残差序列表现出白噪声特性，最终使用该模型对该地区未来的洪水情况进行预测，为防洪决策提供科学依据。

五、总结

ACF 自相关法和 PACF 偏自相关法在洪水预测中具有重要作用。ACF 能够揭示洪水时间序列的自相关模式，帮助我们了解洪水的平稳性和季节性等特征；PACF 则侧重于反映序列之间的直接相关性，为自回归模型的阶数选择提供依据。通过联合运用 ACF 和 PACF，可以更准确地识别洪水时间序列的统计特性，建立合适的预测模型，提高洪水预测的精度，从而为防洪减灾工作提供有力支持。在未来的研究中，我们还可以结合其他先进的数据分析方法和模型，进一步优化洪水预测技术，更好地应对洪水灾害带来的挑战。