强化学习笔记1——DQN实现CartPole小游戏（代码分析）

1.环境介绍

环境是用的gym中的CartPole-v1，就是火柴棒倒立摆。需要提前安装gymnasium。

import gymnasium as gym

state:状态观测值有四个，就是小车的位置，即小车的位置，速度，倾斜角度和角度的变化速度。当位置和角度倾斜超出范围，则环境终止。

这里返回一个{ndarray{4，}}的类型，分别代表小车的位置，速度，角度，和角度变化率。

---

action：环境的动作是一维的，能取两个值0和1。取0代表把小车往左移动，取1代表把小车往右边移动。env.step(action)表示执行动作，函数会返回下一个状态st+1，奖励值reward，以及环境终止符done。

env.step(0)#小车往左
env.step(1)#小车往右

---

reward： 环境的奖励设置是每个时步下能维持杆不到就给一个 +1 的奖励，因此理论上在最优策略下这个环境是没有终止状态的，因为最优策略下可以一直保持杆不倒。但是基于 TD 的算法都必须要求环境有一个终止状态，所以在这里设置了一个环境的最大步数，超出最大步数则done=true。

---

常用代码：

导入库：import gymnasium as gym

创造环境：env = gym.make('env_name')

重置环境，并返回一个状态：state, info = env.reset(seed) 

2.DQN

DQN使用神经网络来近似值函数，即神经网络的输入是state s,输出是Q(s,a),∀a∈AQ(s,a),∀a∈A (action space)。通过神经网络计算出值函数后，DQN使用ϵ−greedy策略来输出action。值函数网络与ϵ−greedy策略之间的联系是这样的：首先环境会给出一个obs，智能体根据值函数网络得到关于这个obs的所有Q(s,a)。环境接收到此action后会给出一个奖励reward及下一个obs。这是一个step。此时我们根据reward去更新值函数网络的参数。接着进入下一个step。如此循环下去，直到我们训练出了一个好的值函数网络。

以下是DQN算法的伪代码：

2.1经验回放

 采用经验回放的原因：

1所有的四元组(st,at,rt,st+1)在用完之后就丢掉了，造成经验的浪费。(实际上这里代码保存的是五元组，还有环境的终止符done，因为DQN在估计Q值的时候需要用到这个终止符)

2.t时刻的四元组为(st,at,rt,st+1)，更新策略的时候，st和st+1有很强相关性，这种相关性实际上是有害的，我们希望打散这种相关性，从而使得训练效果更好。

class ReplayBuffer(object):
    def __init__(self, capacity: int) -> None:
        self.capacity = capacity
        self.buffer = deque(maxlen=self.capacity)
    def push(self,transitions):
        ''' 存储transition到经验回放中
        '''
        self.buffer.append(transitions)
    def sample(self, batch_size: int, sequential: bool = False):
        if batch_size > len(self.buffer): # 如果批量大小大于经验回放的容量，则取经验回放的容量
            batch_size = len(self.buffer)
        if sequential: # 顺序采样
            rand = random.randint(0, len(self.buffer) - batch_size)
            batch = [self.buffer[i] for i in range(rand, rand + batch_size)]
            return zip(*batch)
        else: # 随机采样
            batch = random.sample(self.buffer, batch_size)
            return zip(*batch)
    def clear(self):
        ''' 清空经验回放
        '''
        self.buffer.clear()
    def __len__(self):
        ''' 返回当前存储的量
        '''
        return len(self.buffer)

经验回放有很多写法，这里用的是一个双端队列。

2.2ϵ−greedy策略

贪心动作总是最大化眼前的收益，不去尝试。ϵ−greedy选择以ϵ概率随机尝试，剩下的概率贪心来选取动作。非常简单的平衡探索(Explotation)和利用(Exploitation)的思想是通过确保整个过程随机来实现的。实际上就是随机和贪心相结合。在前期增强了探索增加探索性，后期减少探索增加训练稳定性。

举个例子，机器去学一个未知的东西，它用一个复杂的方法完成了它，但是呢它故步自封不去采取新的方案，一直以为那个方案好，这就是陷入了局部最优，前期没有探索就只会在一个很局限的区域去选择固定的狭隘方案，难以得到好的训练效果。同样的，后期探索多就得不到一个稳定的训练成果。

    def sample_action(self,state):#采样动作
        self.sample_count+=1
        self.epsilon = self.epsilon_end + (self.epsilon_start - self.epsilon_end) * \
                       math.exp(-1. * self.sample_count / self.epsilon_decay)
        if random.random()>self.epsilon:
            with torch.no_grad():
                state=torch.tensor(state,device=self.device,dtype=torch.float32).unsqueeze(dim=0)
                q_values=self.policy_net(state)
                action=q_values.max(1)[1].item()#用训练好的策略选取最大Q的动作
        else:
            action=random.randrange(self.action_dim)#随机选取动作
        return action

2.3目标网络

DQN算法通过缩小当前Q值和目标Q值之间的loss来更新网络：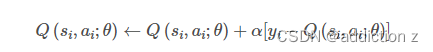

如果当前有个小批量样本导致模型对 Q 值进行了较差的过估计，如果接下来从经验回放中提取到的样本正好连续几个都这样的，很有可能导致 Q 值的发散。

因此引入了一个目标网络：

目标网络和当前网络结构都是相同的，都用于近似 Q 值，在实践中每隔若干步才把每步更新的当前网络参数复制给目标网络，这样做的好处是保证训练的稳定，避免 Q 值的估计发散。这个技巧其实借鉴了 Double DQN 算法中的思路。

这里的目标网络好比公司的CEO，因为要对当前Q值做出比较合理的估计（提供给手下较为正确的命令），所以他不能着急做决策，需要先收集手下给的各个情报，在手下收集了若干步的情报后再去改变自己的策略，以便能对手下发出更好的号令来更新手下的策略。

2.4模型结构

采用的是MLP前馈神经网络，输入一个状态维度的张量，返回一个动作维度的张量，输出张量的每一个维度代表那个动作的q值。

class MLP(nn.Module):
    def __init__(self,state_dim,action_dim,hidden_dim=128):
        super(MLP,self).__init__()
        self.fc1=nn.Linear(state_dim,hidden_dim)
        self.fc2=nn.Linear(hidden_dim,hidden_dim)
        self.fc3=nn.Linear(hidden_dim,action_dim)
    def forward(self,x):
        x=F.relu(self.fc1(x))
        x=F.relu(self.fc2(x))
        return self.fc3(x)

模型结构要根据实际情况去选，我见过的强化学习模型用的比较多的是MLP模型。此外卷积模型常用于图像分类，因为图像返回一个多维的张量（height*weight*3，3是rgb图像的特征），可以更好处理图像信息。

2.5网络训练

def train(cfg, env, agent):
    ''' 训练
    '''
    print("开始训练！")
    rewards = []  # 记录所有回合的奖励
    steps = []
    for i_ep in range(cfg.train_eps):
        ep_reward = 0  # 记录一回合内的奖励
        ep_step = 0
        state, info = env.reset(seed = cfg.seed)  # 重置环境，返回初始状态
        for _ in range(cfg.max_steps):
            ep_step += 1
            action = agent.sample_action(state)  # 选择动作
            next_state, reward, terminated, truncated , info = env.step(action)  # 更新环境，返回transition
            agent.memory.push((state, action, reward, next_state, terminated))  # 保存transition
            state = next_state  # 更新下一个状态
            agent.update()  # 更新智能体
            ep_reward += reward  # 累加奖励
            if terminated:
                break
        if (i_ep + 1) % cfg.target_update == 0:  # 智能体目标网络更新
            agent.target_net.load_state_dict(agent.policy_net.state_dict())
        steps.append(ep_step)
        rewards.append(ep_reward)
        if (i_ep + 1) % 10 == 0:
            print(f"回合：{i_ep+1}/{cfg.train_eps}，奖励：{ep_reward:.2f}，Epislon：{agent.epsilon:.3f}")
    print("完成训练！")
    env.close()
    return {'rewards':rewards}

在每个训练回合里：不断通过ϵ−greedy策略来选取动作直到环境返回done，但因为这里训练到后期环境并不会返回done，设置了一个max_steps=200，执行200次动作后自动返回done。奖励的计算是在一个回合中执行的所有动作的奖励和。

此外训练的频率是每执行一个动作训练一次，以下是训练的代码：

    def update(self):
        if len(self.memory)<self.batch_size:#经验回放中不满足一个批量时，不更新策略
            return
        state_batch,action_batch,reward_batch,next_state_batch,done_batch=self.memory.sample(self.batch_size)
        #将数据转换为tensor
        state_batch=torch.tensor(np.array(state_batch),device=self.device,dtype=torch.float)
        action_batch=torch.tensor(action_batch,device=self.device).unsqueeze(1)
        reward_batch = torch.tensor(reward_batch, device=self.device, dtype=torch.float)
        next_state_batch = torch.tensor(np.array(next_state_batch), device=self.device, dtype=torch.float)
        done_batch = torch.tensor(np.float32(done_batch), device=self.device)
        q_values = self.policy_net(state_batch).gather(dim=1, index=action_batch)  # 计算当前状态(s_t,a)对应的Q(s_t, a)
        next_q_values = self.target_net(next_state_batch).max(1)[0].detach()  # 计算下一时刻的状态(s_t_,a)对应的Q值
        # 计算期望的Q值，对于终止状态，此时done_batch[0]=1, 对应的expected_q_value等于reward
        expected_q_values = reward_batch + self.gamma * next_q_values * (1 - done_batch)
        loss = nn.MSELoss()(q_values, expected_q_values.unsqueeze(1))  # 计算均方根损失
        # 优化更新模型
        self.optimizer.zero_grad()
        loss.backward()
        # clip防止梯度爆炸
        for param in self.policy_net.parameters():
            param.grad.data.clamp_(-1, 1)
        self.optimizer.step()

刚从replay buffer中取出来时，state_batch,action_batch,reward_batch,next_state_batch,done_batch都是一个batch_size大小的元组，为了方便训练先要把他们转换为Tensor张量。

state_batch本来是batch_size大小的元组，每个元素都是一个四维的张量，np.array(state_batch)把它转化成一个（batch_size，state_dim）大小的array，再将他转换成tensor（batch_size，state_dim）。

action_batch也是一个batch_size大小的元组每个元素都是一个数字（0或1），代表取的动作。unsqueeze(1)能增加一个维度，确保tensor中每个分量都是tensor而不是一个数。

q_values = self.policy_net(state_batch).gather(dim=1, index=action_batch)代表当前状态对应执行了动作的q值。其中self.policy_net(state_batch)返回一个（batch_size，action_dim）大小的张量，.gather(dim=1, index=action_batch)则从这个张量的第一个维度（列），根据实际执行的action，从action_dim这个维度上选取对应action的q值，最后返回一个（batch_size，1）的值。

next_q_values = self.target_net(next_state_batch).max(1)[0].detach()则是在st+1状态中选取最大值的动作来计算下一个动作的q值。.detach()是分离梯度的操作，pytorch中如果希望这个变量的梯度不被计算，则把它分离出来，这里next_q_values是为了q网络估计出来的q_values更准确，本身梯度不应该被计算，因此这个变量在loss中被看作常数。

各个变量的维度和取值：（batch_size=64，state_dim=4）

2.5结果

经过100回合的训练，最后模型收敛

并且经过测试，小车已经能稳定在200步的移动中保持不倒：

通过gym提供的rab_array可以把游戏的每一帧保存下来。最后可以通过imageio库来变成动图保存。

import imageio
    env = gym.make('CartPole-v1', render_mode='rgb_array')
    save_path = 'path'
    gif_filename = 'cartpole_rendering.gif'
    os.makedirs(save_path, exist_ok=True)
    frames = []#设置动图的帧列表
    # 重置环境
    state,info= env.reset(seed = cfg.seed)

    for step in range(cfg.max_steps):
        # 渲染当前帧
        render_frame = env.render()
        frames.append(render_frame)
        action = agent.predict_action(state)
        next_state, reward, terminated, truncated, info = env.step(action)  # 更新环境，返回transition
        state = next_state  # 更新下一个状态

        # 如果游戏结束，退出循环
        if terminated:
            break

    imageio.mimsave(os.path.join(save_path, gif_filename), frames)

动图效果如下，可以看到小车已经可以在设定的步数内保持平衡了！

 

2.6超参数

超参数的设置如下。通过测试，batch_size，gamma（微小改动的影响也很大），episilon的设置，目标网络更新频率对模型的训练都有很大的影响。

class Config:
    def __init__(self) -> None:
        self.algo_name = 'DQN'  # 算法名称
        self.env_id = 'CartPole-v1'  # 环境id
        self.seed = 1  # 随机种子，便于复现，0表示不设置
        self.train_eps = 100  # 训练的回合数
        self.test_eps = 20  # 测试的回合数
        self.max_steps = 200  # 每个回合的最大步数，超过该数则游戏强制终止
        self.gamma = 0.95  # 折扣因子
        self.epsilon_start = 0.95  # e-greedy策略中初始epsilon
        self.epsilon_end = 0.01  # e-greedy策略中的终止epsilon
        self.epsilon_decay = 500  # e-greedy策略中epsilon的衰减率
        self.memory_capacity = 100000  # 经验回放池的容量
        self.hidden_dim = 256  # 神经网络的隐藏层维度
        self.batch_size = 64  # 批次大小
        self.target_update = 4  # 目标网络的更新频率
        self.lr = 0.0001  # 学习率
        self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")  # 检测gpu