机器学习---线性回归、Logistic回归问题相关笔记及实现

回归问题

概述：

回归问题就是预测一个连续问题的数值，比如……，

而如果将上面的回归问题，利用Sigmoid函数(Logistic 回归)，能将预测值变为判断是否能做某事情的概率，将回归得到的连续数值变为（0，1）之间的概率，然后可以用于处理二分类问题

一元线性回归

线性回归方程为：
$$\hat{y}=ax+b$$
比如给定一组数据，可以得到如下的散点图。

x=np.array([1,2,4,6,8])
y=np.array([2,5,7,8,9])

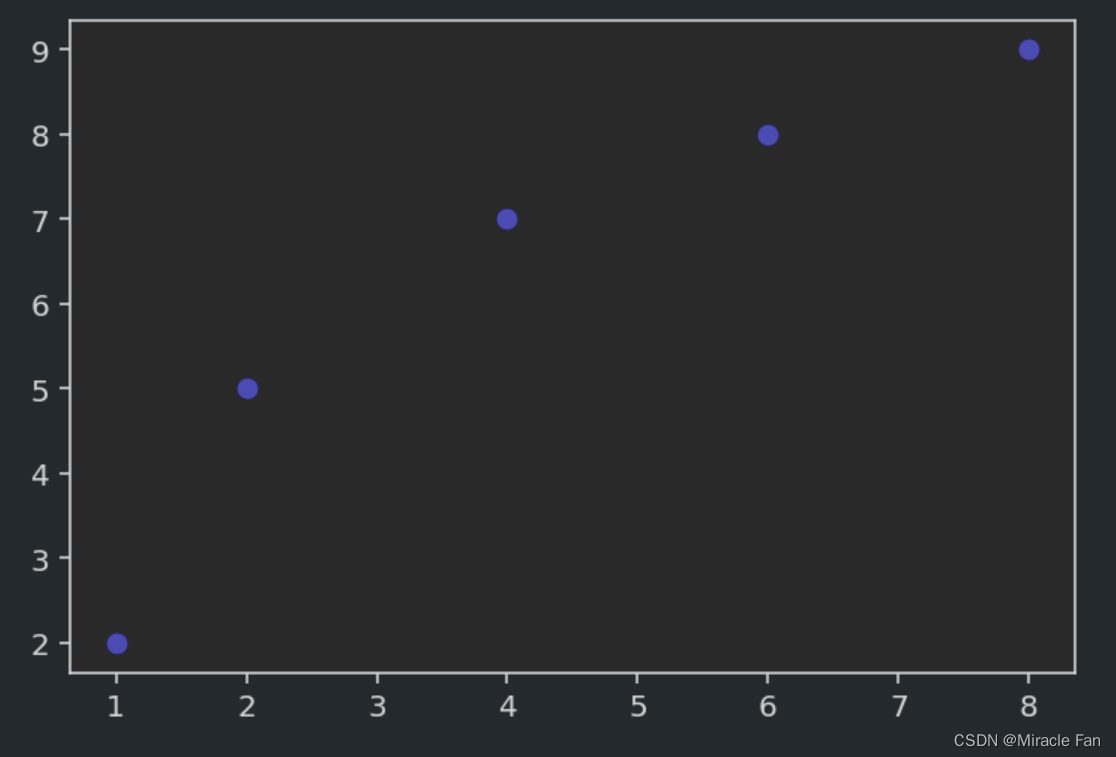
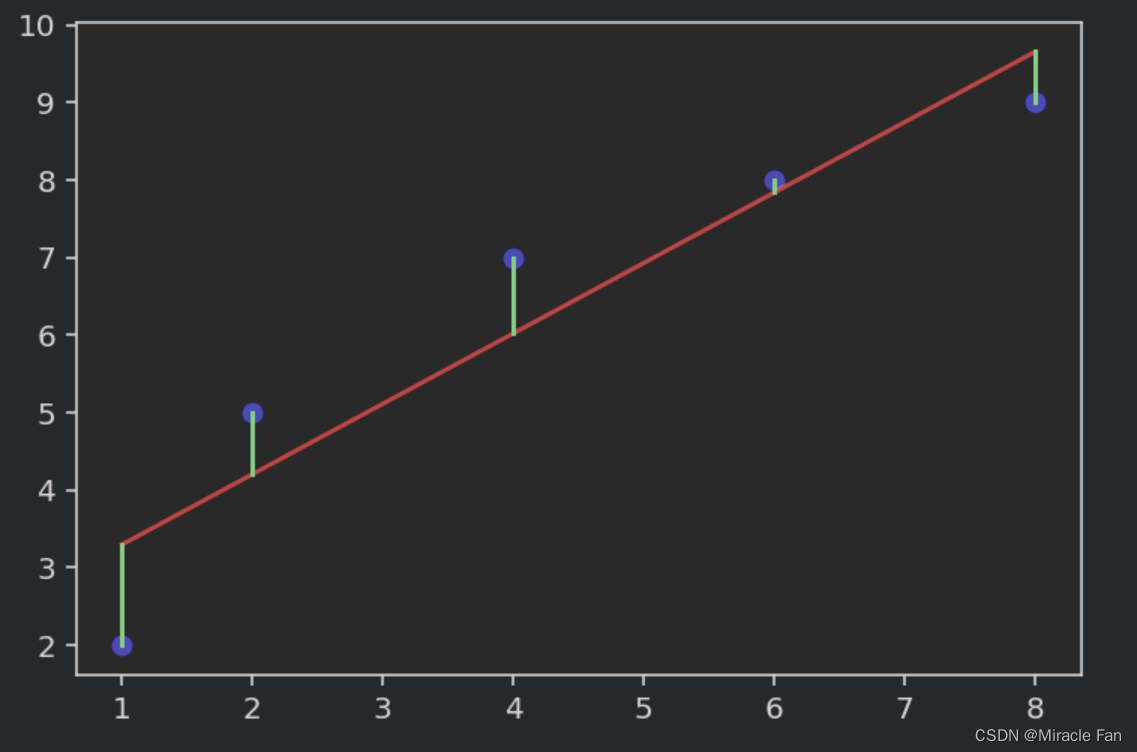
为了进行线性回归，相当于我们拟合出一条直线，能很好地去连接上图中各个样本，但是一般情况下是达不到完美的拟合效果的，只是希望如下图所示，绿色的线表示预测点与真实点之间的误差，我们希望误差尽可能的小，也就是能达到较好的拟合效果了。

y_pred=lambda x: a*x+b
plt.scatter(x,y,color='b')
plt.plot(x,y_pred(x),color='r')
plt.plot([x,x], [y,y_pred(x)], color='g')
plt.show()

也就是可以定义一个损失函数：
$$L=\frac{1}{n}\sum _{i=1}^n(y^i-y_{pred}^i)$$
但是如果选用该函数，当我们进行误差计算时，某些情况下预测值大于真实值，某些情况下预测值小于真实值。则会导致$y-y_{pred}$出现正、负的情况，而将他们相加的时候，则会导致相互抵消，所以这里我们需要采用均方损失函数：
$$L=\frac{1}{n}\sum _{i=1}^n(y^i-y_{pred}^i{)}^2$$
代入拟合方程：
$$L=\frac{1}{n}\sum _{i=1}^n(y^i-a{x}^i-b{)}^2$$
利用最小二乘法推导法则：
$$\begin{gathered} a=\frac{{\sum }_{i=1}^n(x_i-\bar{x})(y^i-\bar{y})}{{\sum }_{i=1}^n(x^i-\bar{x}{)}^2} \\ b=\bar{y}-a\bar{x} \end{gathered}$$

def Linear_Regression(x,y):
    x_mean=np.mean(x)
    y_mean=np.mean(y)
    # num=np.sum((x-np.tile(x_mean,x.shape))*(y-np.tile(y_mean,y.shape)))
    num=np.sum((x-x_mean)*(y-y_mean))
    den=np.sum((x-x_mean)**2)
    a=num/den
    b=y_mean-a*x_mean
    return a,b

由于numpy的广播机制，此处不必将x_mean的维度进行调整。

多元线性回归

对于多元线性回归，其一般表达式为：
$$y={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\cdots +{\theta }_n{x}_n$$
这个公式可以简化为：
$$Y=\theta \cdot X$$

$$X=\left(\begin{array}{cccc}1& x_{11}& \cdots & x_{1p}\\ 1& x_{21}& \cdots & x_{2p}\\ ⋮& ⋮& \ddots & ⋮\\ 1& x_{n1}& \cdots & x_{np}\end{array}\right)$$

$$\theta =\left(\begin{array}{c}{\theta }_0\\ {\theta }_1\\ {\theta }_2\\ \dots \\ {\theta }_n\end{array}\right)$$

而对于$\theta$的求解，利用于前文的最小二乘法，可以得到：
$$\theta =(X_i^T{X}_i{)}^{-1}{X}_i^{T}y$$

#生成一列用于操作截距值
ones = np.ones((X_train.shape[0], 1))
#在horizental方向上进行堆叠
X_b = np.hstack((ones, X_train))  # 将X矩阵转为第一列为1，其余不变的X_b矩阵
theta = linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
interception = theta[0]
coef =theta[1:]

logistic回归

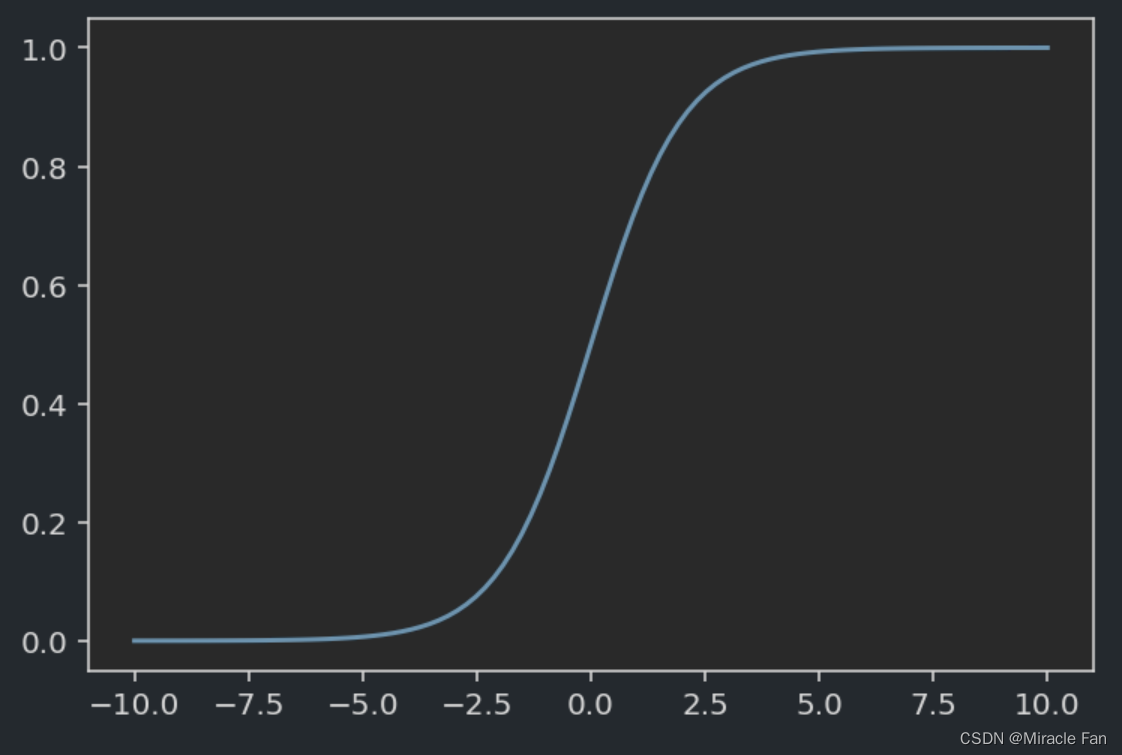
简单的logistics回归就是在线性回归的基础上加上Sigmoid函数，实现对预测结果的压缩，使之保持在（0，1）之间也就是可以理解成概率值，然后通常以0.5作为分界线，概率大于0.5则为类别1反之为0.

用于将利用线性回归得到的概率问题利用sigmoid函数输出为类别问题。
$$p=\frac{1}{1+e^{-z}}$$

• z：一般为线性回归方程
• p:预测得到的概率，通过分界线判断属于哪一类

梯度下降

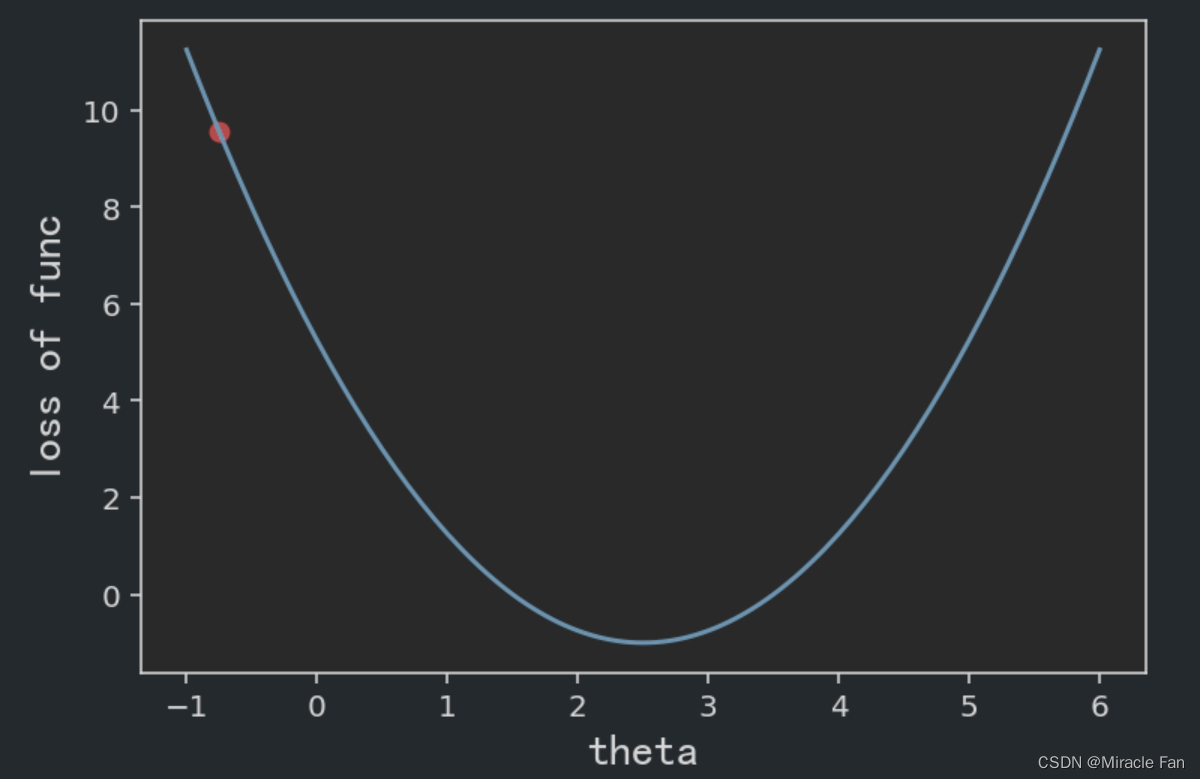
梯度下降法主要是应用在对损失函数的优化上，找到loss值最小的参数值。

比如假设一个损失函数为
$$L=(x-2.5{)}^2-1$$

然后定义其损失函数及其导数。

def J(theta):
    try:
        return (theta-2.5)**2-1
    except:
        return float('inf')
def dJ(theta):
    return 2*(theta-2.5)

每一次迭代
$$\theta =\theta +\eta \frac{dJ}{\theta }$$

def CalGradient(eta):
    theta = 0.0
    theta_history = [theta]
    epsilon = 1e-8#用于最终终止梯度下降的计算
    while True:
        gradient = dJ(theta)
        last_theta = theta
        theta = theta - eta * gradient
        theta_history.append(theta)
        if (abs(J(theta) - J(last_theta)) < epsilon):
            break

    plt.title('lr:' + str(eta))
    plt.plot(x, J(x), color='r')
    plt.plot(np.array(theta_history), J(np.array(theta_history)), color='b', marker='x')
    plt.show()
    print(len(theta_history))

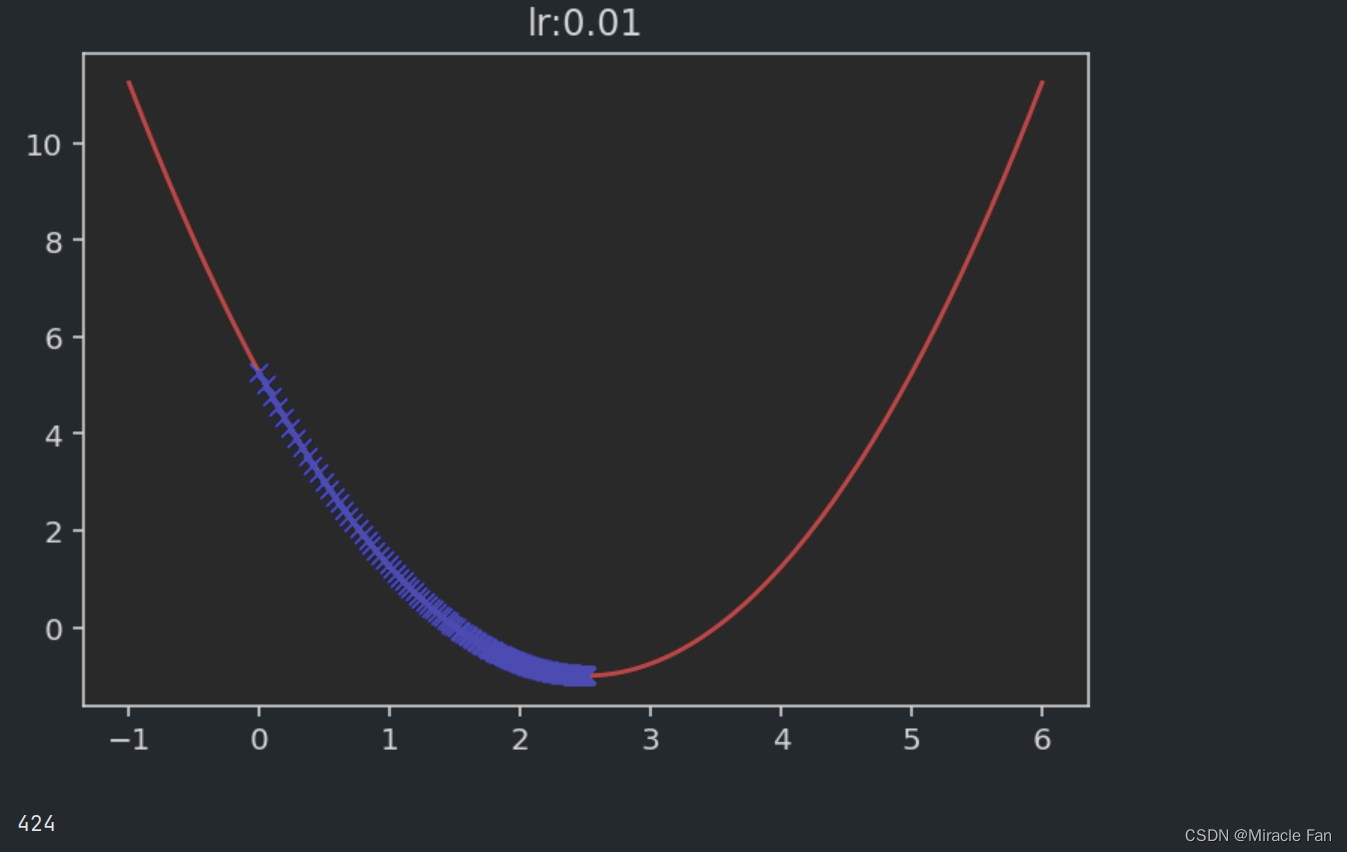
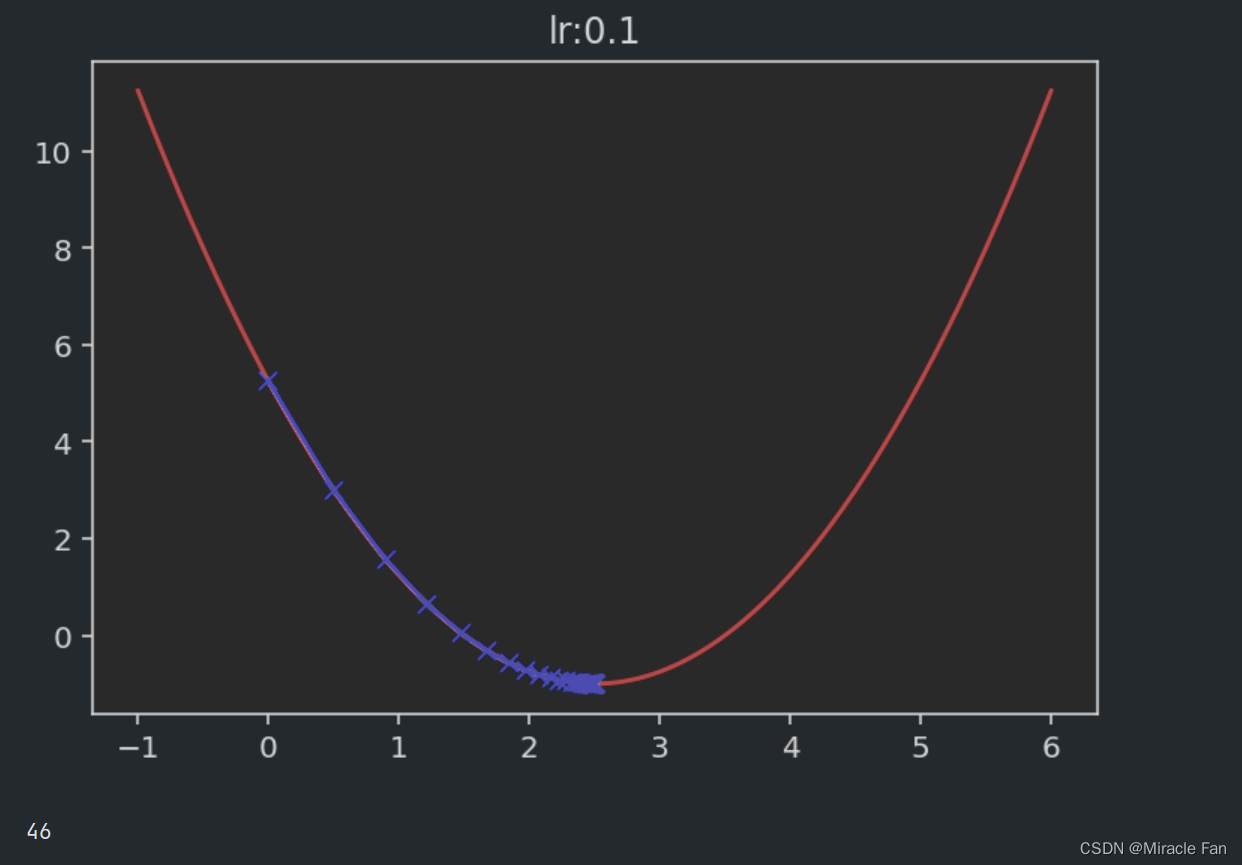
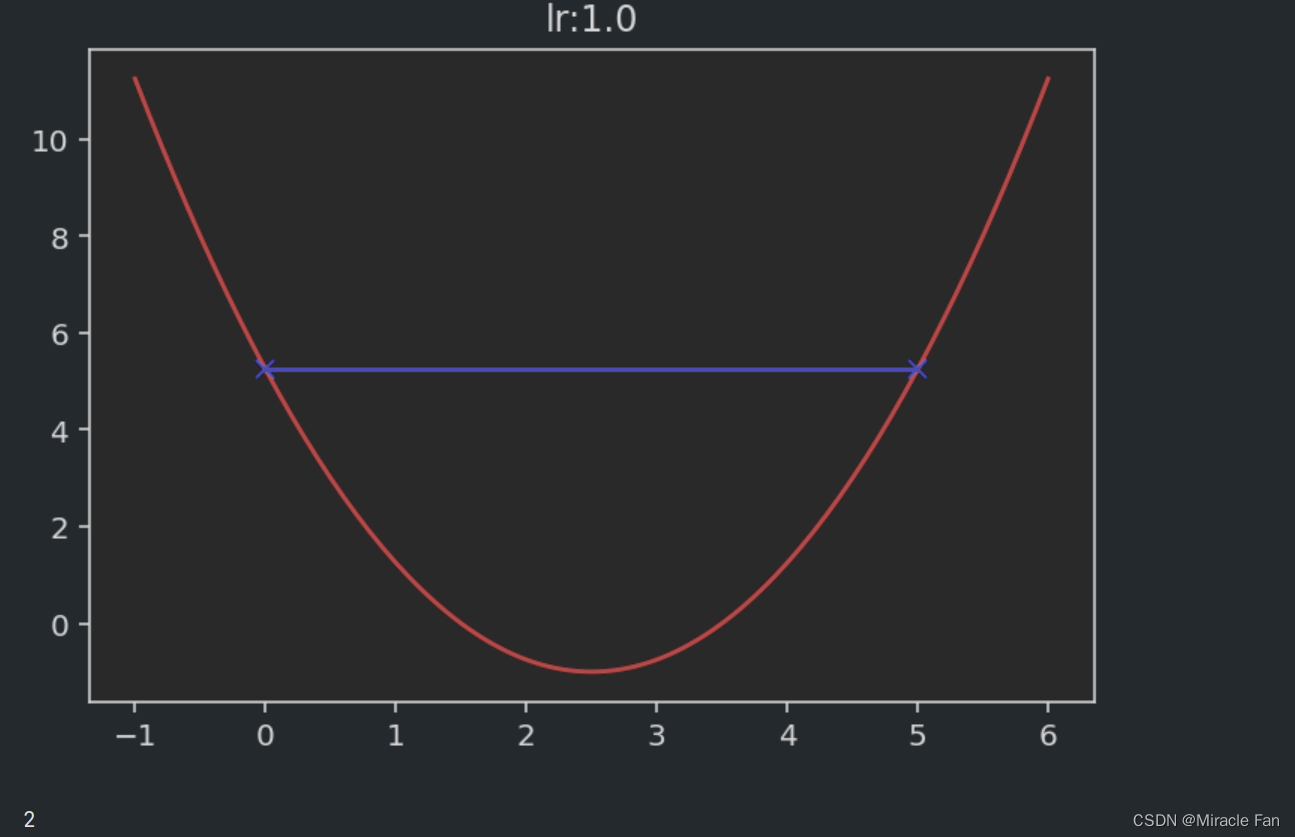
相关的取不同的学习率时，下降图如下所示。学习率一般在0~1之间，如下图当学习率为1时，已经达不到收敛状态，而当学习率大于1时，其会呈现一个发散的状态。

Logistic回归的损失函数

Logistic回归将线性回归融入后的表达式如下所示：
$$p=\frac{1}{1+e^{-\theta X}}$$
对于Logistic回归，一般采用的是对数损失函数，进行参数的计算。

$$cost=\{\begin{array}{cc}-{\log }^{(p_{pred})}if& y=1\\ -{\log }^{(1-p_{pred})}if& y=0\end{array}$$

稍作整理可以合成一个损失函数：
$$cost=-y\log (p_{pred})-(1-y)\log (1-p_{pred})$$

import numpy as np

class LogisticRegression:

    def __init__(self):
        self.coef_ = None
        self.intercept_ = None
        self._theta = None

    def _sigmoid(self, x):
        y = 1.0 / (1.0 + np.exp(-x))
        return y

    def fit(self, x_train, y_train, eta=0.01, n_iters=1e4):
        assert x_train.shape[0] == y_train.shape[0], '训练集和其标签长度样本数量需要一一致'

        def J(theta, x, y):
            p_pred = self._sigmoid(x.dot(theta))
            try:
                return -np.sum(y * np.log(p_pred) + (1 - y) * np.log(1 - p_pred)) / len(y)
            except:
                return float('inf')

        def dJ(theta, x, y):
            x = self._sigmoid(x.dot(theta))
            return x.dot(x - y) / len(x)

            # 模拟梯度下降

        def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
            theta = initial_theta
            i_iter = 0
            while i_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta * gradient
                i_iter += 1
                if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                    break
            return theta

        X_b = np.hstack([np.ones((len(x_train), 1)), x_train])
        initial_theta = np.zeros(X_b.shape[1])  # 列向量
        self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)
        self.intercept_ = self._theta[0]  # 截距
        self.coef_ = self._theta[1:]  # 维度
        return self

    def predict_proba(self, X_predict):
        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return self._sigmoid(X_b.dot(self._theta))

    def predict(self, X_predict):
        proba = self.predict_proba(X_predict)
        return np.array(proba > 0.5, dtype='int')