数学建模案例--基于微分方程的酒后驾车问题浅析

最新推荐文章于 2024-10-19 10:51:43 发布

灰楚楚

最新推荐文章于 2024-10-19 10:51:43 发布

阅读量1w

点赞数 20

文章标签：经验分享

本文链接：https://blog.csdn.net/qq_49775724/article/details/122872990

版权

数学建模案例复现1--基于微分方程的酒后驾车问题浅析

撰文缘由
模型建立
代码区

撰文缘由

笔者在撰写本文前不得不说一下，B站里面的确有许许多多的宝藏UP主，本人也是在听入迷了相关饮酒驾车建模视频的前提下心中油然而生写作热情。因此本文只是相关视频的代码复现，并会在相应基础上进行一定程度的拓展。
笔者简介：CCNU计算机科学与技术jdb大二一员，也喜欢日漫唱歌梅老板和弹钢琴。
原视频名称:数学建模案例 6 饮酒驾驶的问题
(https://www.bilibili.com/video/BV1MR4y1g7ns?spm_id_from=333.999.0.0)

模型建立

在建立模型前我们作出合理假设:
1）人体体液中酒精浓度与血液中酒精浓度相同。
2）人体自身产生的酒精忽略不计，即正常不饮酒情况下，人体体液中的酒精浓度看作0。
3）人体体液对酒精吸收速度与当前肠胃中酒精含量成正比，比例系数为a。
4）酒精代谢速度与当前体液中酒精含量成正比，比例系数为b。
5）整个过程中人没有摄入任何影响代谢的药物和作剧烈运动。
6）人体的吸收率和代谢率是恒定的。
7）一瓶啤酒中约含酒精21700mg。
8）体重为70kg的人体液体积约为420（其中每单位100ml）。

“一口气”饮酒模型

饮酒模型的建模示意图
下面我们对模型的参数进行说明:
1.Q:饮酒酒桶所含酒精量大小。
2.y(t):肠胃中所含酒精量(随时间变量t变化)。
3.x(t):体液中所含酒精量(随时间变量t变化)。
4.c(t):体液中所含酒精浓度(由x(t)/v0得到)。
5.v0:体液体积(其中每单位100ml)。
6.a*y(t):吸收速率(假设与含酒精量成正比关系)。
7.b*y(t):代谢速率(假设与酒精浓度成正比关系)。

所谓“一口气”喝酒的意思就是酒后驾车嫌疑人以迅雷不及掩耳之势抢铃儿响叮当之态喝下了一桶酒，这样的话酒会全部直接进入肠胃中呆着。那这样的话我们就可以开始建立微分方程模型。

我们分别对y(t)和c(t)进行分对象的讨论,对肠胃中的y(t)而言，单位时间中的变化量就是-a*y。于是乎我们可以列出微分方程组进行表示如下:

dy/dt=-a*t
y(0)=Q0 (其中Q0为酒桶中酒量大小，作为初始条件)

对于体液中的酒精浓度c(t)而言,在单位时间里面，你既有从肠胃中输送来的酒精，又有通过新陈代谢消失掉的酒精,那么我们可以得到下面的微分方程组:

dc/dt=a * Q0 * e^(-a*t) / v0 - b * c
c(0)=c0 (其中c0为未饮酒时体液中的酒精浓度，作为初始条件)

你咋一看这a * Q0 * e^(-at)有点陌生捏？
其实a * Q0 * e^(-at)就是上一个方程的y(t)的求解表达式。
准确的说就是dc/dt=a * y(t) / v0-b * c表达式的偷懒但是很精确的表示形式。

对于求解微分方程组你可以手算也可以心算还可以用除了不会生孩子其他啥都会的MATLAB求解，本人用的是MATLAB R2020b版本。

代码段如下表示:

%%一口气饮酒，肠胃与体液中酒精浓度随时间的变化 
dsolve('Dy=-a*y','y(0)=Q','t')%肠胃中酒精浓度的变化
dsolve('Dc=a*Q*exp(-a*t)/v0-b*c','c(0)=c0','t')%体液中酒精浓度的变化

得到的体液中的酒精浓度表达式就是:
c(t)=e ^ (-b * t)* (c0 + (Q * a) / (v0 * (a - b))) - (Q * a * e(b * t - a * t) * e^(-b * t))/(v0*(a - b))

不过这样的形式也太复杂了吧，但是我们可以利用案例中的数据进行曲线拟合，并且利用lsqcurvefit()函数求出正比例系数a和b。下面是案例的数据展示:

监测时间(h)	体液中酒精浓度(mg/100ml)
0.25	30
0.5	68
0.75	75
1	82
1.5	82
2	77
2.5	68
3	68
3.5	58
4	51
4.5	50
5	41
6	38
7	35
8	28
9	25
10	18
11	15
12	12
13	10
14	7
15	7
16	4

我们不妨取Q0=3*21700（一口气3瓶啤酒的量！），v0=420，c0=0的初始参数条件值，经过拟合参数a,b之后作出监测时间与体液中酒精浓度的曲线图如下:
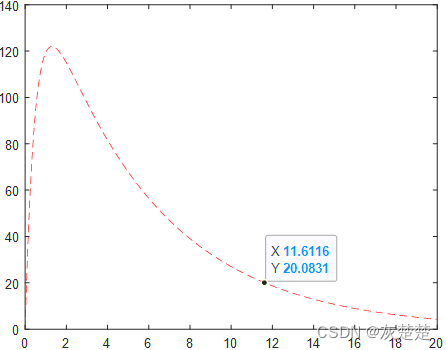
在这里插入图片描述
如果以20mg/(100ml)的量为界线，那我们知道该同志饮酒一次后至少需要12小时左右才能够恢复到正常状态。