集合中的质数(容斥原理)

集合中的质数

就是求$|A_1\cup A_2\cup A_3...\cup A_n|,其中A_i表示a_i的倍数的个数。$

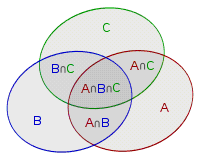
$如图|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|,这是最基础的容斥，可以推广到n个集合的容斥：$
$$|A_1\cup A_2\cup A_3...\cup A_n|=\sum |A_i|-\sum |A_i\cap A_j|+\sum |A_i\cap A_j\cap A_k|-...+(-1{)}^{n-1}\sum |A_1\cap A_2\cap ....\cap A_n|$$$可以看出奇加偶减,设f(a_i,a_j...a_k)为1-m中，a_i,a_j...a_k的倍数的个数,则f(a_i)=\frac{m}{a_i},f(a_i,a_j...a_k)=\frac{m}{lcm(a_i,a_j...a_k)},本题a_i是质数，所以lcm就是\prod a_i$
这里用的二进制枚举，设一个n位二进制数，第i位取0，1分别表示不是$a_i$倍数和是$a_i$倍数，那么一共有$2^n-1$(至少是一个数的倍数)种状态，遍历一遍就好了。

#include <iostream>
#include <cstring>
#include <cmath>
#include <bitset>
#include <queue>
#include <vector>
#include <cstdio>
#include <set>
#include <stack>
#include <sstream>
#include <cstring>
#include <algorithm>
#include <map>
#define rep(i, a, b) for (long long i= a; i <= b; i++)
#define reps(i, a, b) for (long long i = a; i >= b; i--)
#define gcd(a,b) __gcd(a,b)
#define lcm(a,b) a*b/gcd(a,b)
#define ls(node) tree[node].ls
#define rs(node) tree[node].rs
#define val(node) tree[node].val
#define sum(node) tree[node].sum
#define lazy(node) tree[node].lazy
#define lazy1(node) tree[node].lazy1
#define lazy2(node) tree[node].lazy2
#define tr(node) tree[node]
using namespace std;
const int N=1e6+7;
const int inf=0x3f3f3f3f;
const int mod=1e9+7;
typedef long long ll;
#define Rep(i,a,b)for(ll i=a;i<=b;i++)
int a[N];
ll solve(int n,int m)
{
    ll ans=0;
    for(int i=1;i<(1<<n);i++){//枚举每一种情况
        ll cnt=0,lcm=1;
        for(int j=0;j<n;j++){
            if(1<<j&i){//判断第j位是不是1
                cnt++;
                lcm*=a[j+1];//因为我的数组从1开始的所以是j+1
            }
        }
        if(cnt&1)ans+=m/lcm;//奇加偶减
        else ans-=m/lcm;
    }
    return ans;
}
int main()
{
    ll n,m;
    scanf("%lld%lld",&n,&m);
    rep(i,1,n)scanf("%d",&a[i]);
    printf("%lld\n",solve(n,m));
    return 0;
}