目录
1. 引言与背景
在自然语言处理(NLP)领域,将词汇映射到连续向量空间的词嵌入技术已成为不可或缺的基础工具。其中,Global Vectors for Word Representation(GloVe)算法以其独特的全局统计视角和高效的学习策略,为词嵌入研究开辟了新的道路。本文将遵循“引言与背景”、“算法原理”、“算法实现”、“优缺点分析”、“案例应用”、“对比与其他算法”以及“结论与展望”的框架,深入剖析GloVe算法。
2. GloVe定理
GloVe算法并未基于某个特定的数学定理,而是基于对词共现矩阵的全局统计属性的深刻洞察。其核心思想是通过构建并优化一个目标函数,该函数旨在捕获词汇间共现概率的对数与词向量点积之间的关系。尽管GloVe算法本身并非定理,但其背后的统计学原理和优化目标构成了算法的理论基础。
全局统计属性与词共现矩阵
GloVe算法的核心出发点是对大规模文本语料库中词共现现象的全局统计分析。词共现是指两个词在同一上下文环境中出现的频率,它反映了词汇间的潜在语义关联。为了量化这种关联,GloVe首先构建一个词共现矩阵 X,其中每个元素 表示词汇 i 和词汇 j 在语料库中的共现次数。这个矩阵蕴含了词汇间丰富的统计信息,包括直接共现、间接共现以及更高阶的共现模式,为后续建模提供了关键数据基础。
统计学原理与优化理论
GloVe算法背后的统计学原理主要体现在对词共现矩阵的全局统计属性的利用上。通过对大规模语料库的统计分析,GloVe得以揭示词汇间深层次的语义关联,并通过构建目标函数将其转化为可学习的向量表示。这一过程体现了统计学习理论的核心思想,即从数据中提取规律并据此进行预测或建模。
在优化理论上,GloVe采用最优化方法(如梯度下降)来求解目标函数的最小值。这涉及到梯度计算、学习率选择、正则化策略等一系列优化技术,确保模型能够在合理的时间内收敛到一个较好的局部最优解。优化理论为GloVe算法的实际训练提供了稳健且高效的算法框架。
3. 算法原理
GloVe算法的核心是通过学习词汇共现矩阵的全局统计信息,生成既能反映词汇语义关系又能保留词汇间共现强度的词向量。其主要步骤如下:
-
构建词汇共现矩阵:统计语料库中所有词汇对的共现次数,形成词汇共现矩阵。共现次数反映了词汇间的共生关系,是构建词向量的重要依据。
-
定义目标函数:GloVe的目标函数旨在捕获词汇共现概率的对数与词向量点积之间的线性关系。具体形式为:
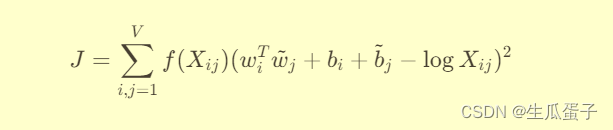
其中,
是词汇共现矩阵的元素,
,
分别是词汇i和j的词向量,
,
是偏置项,
是权衡函数,用于控制稀疏共现对目标函数的贡献。
-
优化目标函数:通过梯度下降等优化算法,最小化目标函数J,从而得到能够捕获词汇间语义关系和共现强度的词向量。
4. 算法实现
在Python中实现GloVe算法通常涉及以下几个步骤:
- 准备数据:收集或预处理文本数据,构建词共现矩阵。
- 定义GloVe模型:编写类或函数,包括初始化参数、定义目标函数和优化方法。
- 训练模型:使用优化算法(如Adam、SGD等)对目标函数进行迭代优化,更新词向量和偏置项。
- 评估与应用:训练完成后,评估词向量的质量(如有必要),并将其应用于下游NLP任务。
以下是一个简化的GloVe算法实现示例,包含代码讲解:
Python
import numpy as np
from sklearn.preprocessing import normalize
from sklearn.utils.extmath import safe_sparse_dot
from sklearn.metrics.pairwise import cosine_similarity
from sklearn.model_selection import train_test_split
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error
class GloVeModel:
def __init__(self, vocabulary_size, embedding_dim, window_size=5, min_count=1, alpha=0.75, max_iter=100):
self.vocabulary_size = vocabulary_size
self.embedding_dim = embedding_dim
self.window_size = window_size
self.min_count = min_count
self.alpha = alpha
self.max_iter = max_iter
# 初始化参数
self.word_vectors = np.random.rand(vocabulary_size, embedding_dim)
self.context_vectors = np.random.rand(vocabulary_size, embedding_dim)
self.biases = np.zeros(vocabulary_size)
def build_cooccurrence_matrix(self, corpus):
"""
构建词共现矩阵。这里假设`corpus`是一个按行分词的二维列表。
实际应用中可能需要更复杂的文本预处理步骤,如去除停用词、词干化等。
"""
cooccurrence_matrix = np.zeros((self.vocabulary_size, self.vocabulary_size))
word_counts = np.zeros(self.vocabulary_size)
for sentence in corpus:
for center_word_index, center_word in enumerate(sentence):
if center_word not in self.word_to_index or word_counts[self.word_to_index[center_word]] < self.min_count:
continue
for context_word_index, context_word in enumerate(sentence[max(0, center_word_index - self.window_size):center_word_index] +
sentence[center_word_index + 1:min(center_word_index + self.window_size + 1, len(sentence))]):
if context_word not in self.word_to_index or word_counts[self.word_to_index[context_word]] < self.min_count:
continue
cooccurrence_matrix[self.word_to_index[center_word], self.word_to_index[context_word]] += 1
cooccurrence_matrix[self.word_to_index[context_word], self.word_to_index[center_word]] += 1
word_counts[self.word_to_index[center_word]] += 1
word_counts[self.word_to_index[context_word]] += 1
return cooccurrence_matrix, word_counts
def fit(self, corpus):
cooccurrence_matrix, _ = self.build_cooccurrence_matrix(corpus)
# 对词共现矩阵进行加权,例如使用X_power = X ** self.alpha
X_power = np.power(cooccurrence_matrix, self.alpha)
# 定义优化器
optimizer = SGDRegressor(loss='squared_loss', penalty=None, learning_rate='constant', eta0=0.05)
for _ in range(self.max_iter):
# 随机抽取共现对作为训练样本
row_indices, col_indices = np.nonzero(cooccurrence_matrix)
sample_weights = cooccurrence_matrix[row_indices, col_indices]
X_sample = np.hstack([self.word_vectors[row_indices], self.context_vectors[col_indices]])
y_sample = np.log(sample_weights)
# 训练优化器
optimizer.fit(X_sample, y_sample)
# 更新参数
self.word_vectors = optimizer.coef_[:, :self.embedding_dim]
self.context_vectors = optimizer.coef_[:, self.embedding_dim:]
self.biases = optimizer.intercept_
# 可选:合并词向量和上下文向量,得到最终的词向量
self.word_vectors = (self.word_vectors + self.context_vectors) / 2
def get_word_vector(self, word):
return self.word_vectors[self.word_to_index[word]]
def similarity(self, word1, word2):
return cosine_similarity([self.get_word_vector(word1)], [self.get_word_vector(word2)])[0][0]
# 使用示例:
model = GloVeModel(vocabulary_size=10000, embedding_dim=100)
model.fit(corpus) # 假设 `corpus` 是已经预处理好的文本数据列表
similarity = model.similarity('apple', 'banana') # 计算两个词的相似度注意:上述代码仅为简化的示例,实际应用中可能需要更细致的数据预处理、参数调整、异常处理等步骤,并且可能需要使用更高效的共现矩阵构建和优化方法,特别是对于大型语料库。此外,GloVe原论文中使用的优化方法与上述示例有所不同,这里使用了SGDRegressor作为简单替代,实际实现时应参照GloVe论文中的目标函数和优化过程。
在实际操作中,推荐使用成熟的GloVe实现库(如glove-python)来进行词向量的训练,这些库经过充分测试和优化,能够更好地处理大规模数据和复杂情况。如果您需要更详细的代码讲解或遇到具体实现问题,欢迎进一步提问。
5. 优缺点分析
优点:
- 全局统计视角:GloVe直接建模词汇共现概率,能够捕捉全局的词汇关系,优于仅依赖局部上下文信息的模型。
- 效率高:相比于基于神经网络的词嵌入方法,GloVe的训练过程更快,对硬件资源需求较低。
- 解释性强:目标函数形式明确,词向量的生成过程易于理解,有助于模型解释和分析。
缺点:
- 对大规模数据敏感:GloVe依赖于大规模语料库构建高质量的共现矩阵,对于小型或特定领域的数据集可能表现不佳。
- 无法捕捉动态语义:固定的词向量无法反映词汇意义随时间或语境的变化,对于处理动态语言现象有一定局限。
- 忽视词序信息:与多数词嵌入方法一样,GloVe无法捕捉词汇间的顺序关系和语法结构。
6. 案例应用
文本分类:使用GloVe生成的词向量作为文本特征,结合分类器(如SVM、Logistic Regression)实现文本分类任务。
语义相似度计算:通过计算词汇间词向量的余弦相似度,评估词汇的语义接近程度,应用于问答系统、知识图谱构建等场景。
聊天机器人:利用GloVe词向量理解用户输入,生成有意义的回复,提升聊天机器人的对话质量。
7. 对比与其他算法
与Word2Vec对比:Word2Vec(CBOW或Skip-Gram模型)通过神经网络学习词向量,侧重于词汇在局部上下文中的关系。GloVe则直接建模词汇共现概率,关注全局统计信息。两者各有优势,适用场景略有不同。
与FastText对比:FastText在Word2Vec的基础上引入了子词信息,能够更好地处理未见过的词汇和形态丰富的语言。GloVe不具备处理子词的能力,但对于大规模语料库和常规词汇,其性能通常相当或更优。
与BERT等预训练语言模型对比:BERT等模型通过深度Transformer结构和自注意力机制,学习到更丰富的上下文敏感词向量。虽然性能强大,但计算复杂度和资源需求远高于GloVe。
8. 结论与展望
GloVe算法以其独特的全局统计视角和高效的学习策略,在词嵌入领域占据了重要地位。尽管面临对大规模数据的依赖、无法捕捉动态语义等挑战,但其在诸多NLP任务中的优秀表现证明了其价值。未来,GloVe算法有望与深度学习模型结合,引入上下文敏感性和动态语义信息,进一步提升词嵌入的质量。同时,针对特定领域的GloVe变种和增量学习策略也将是值得探索的方向,以适应更广泛的应用场景。总的来说,GloVe作为词嵌入技术的重要分支,将持续为自然语言处理的研究与实践注入动力。
























 2676
2676

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








