Data security.隐私保护-Crypten框架各层实现机制

Adongua

已于 2025-04-05 10:22:40 修改

阅读量73

点赞数

分类专栏： # Data security 文章标签：深度学习人工智能隐私保护

于 2023-11-15 15:55:58 首次发布

本文链接：https://blog.csdn.net/qq_51352378/article/details/134408422

版权

Data security 专栏收录该内容

5 篇文章

订阅专栏

Data security.隐私保护-Crypten框架主要实现机制

一、算术秘密分享

用 $[x]=\left \{[x]_p \right\}_{p∈P}$ 来表示x的p方算术秘密分享，其中 $x]_p∈Z/QZ$ ，且满足这些分享的总和可以重构原始值x，即 $x=\sum p∈P[x]p \mod Q$ 。
为了共享一个值x，各方通过PRZS生成一个伪随机零分享，这|P|个随机数的和为0。拥有值x的一方将x添加到生成的分享值中。在添加之前，使用定点编码将x与一个较大的比例因子B相乘并四舍五入到最接近的整数： $x = ro u n d (x B)$ ，其中B=2L，表示L位精度。
为了解密一个值x，通过MPI的reduce操作将各方的分享值收集起来，然后做求和，将得到的结果再解码，即除以比例因子B即可。
代码如下：

class ArithmeticSharedTensor:
    """
    Encrypted tensor object that uses additive sharing to perform computations.

    Additive shares are computed by splitting each value of the input tensor
    into n separate random values that add to the input tensor, where n is
    the number of parties present in the protocol (world_size).
    """
    # constructors:
    def __init__(
        self,
        tensor=None,
        size=None,
        broadcast_size=False,
        precision=None,
        src=0,
        device=None,
    ):
        """
        Creates the shared tensor from the input `tensor` provided by party `src`.

        The other parties can specify a `tensor` or `size` to determine the size
        of the shared tensor object to create. In this case, all parties must
        specify the same (tensor) size to prevent the party's shares from varying
        in size, which leads to undefined behavior.

        Alternatively, the parties can set `broadcast_size` to `True` to have the
        `src` party broadcast the correct size. The parties who do not know the
        tensor size beforehand can provide an empty tensor as input. This is
        guaranteed to produce correct behavior but requires an additional
        communication round.

        The parties can also set the `precision` and `device` for their share of
        the tensor. If `device` is unspecified, it is set to `tensor.device`.
        """

        # do nothing if source is sentinel:
        if src == SENTINEL:
            return

        # assertions on inputs:
        assert (
            isinstance(src, int) and src >= 0 and src < comm.get().get_world_size()
        ), "specified source party does not exist"
        if self.rank == src:
            assert tensor is not None, "source must provide a data tensor"
            if hasattr(tensor, "src"):
                assert (
                    tensor.src == src
                ), "source of data tensor must match source of encryption"
        if not broadcast_size:
            assert (
                tensor is not None or size is not None
            ), "must specify tensor or size, or set broadcast_size"

        # if device is unspecified, try and get it from tensor:
        if device is None and tensor is not None and hasattr(tensor, "device"):
            device = tensor.device

        # encode the input tensor:
        self.encoder = FixedPointEncoder(precision_bits=precision)
        if tensor is not None:
            if is_int_tensor(tensor) and precision != 0:
                tensor = tensor.float()
            tensor = self.encoder.encode(tensor) # 使用定点数编码器对tensor进行编码
            tensor = tensor.to(device=device)
            size = tensor.size()

        # if other parties do not know tensor's size, broadcast the size:
        if broadcast_size:
            size = comm.get().broadcast_obj(size, src)

        # generate pseudo-random zero sharing (PRZS) and add source's tensor:
        self.share = ArithmeticSharedTensor.PRZS(size, device=device).share 
        if self.rank == src:
            self.share += tensor # 将自身这个tensor加上生成的0分享

    @staticmethod
    def PRZS(*size, device=None):
        """
        Generate a Pseudo-random Sharing of Zero (using arithmetic shares)

        This function does so by generating `n` numbers across `n` parties with
        each number being held by exactly 2 parties. One of these parties adds
        this number while the other subtracts this number.
        通过在“n”方之间生成“n”个数字来实现这一点，每个数字恰好由2方持有。其中一方加上这个数字，另一方减去这个数字。
        那么，加入给到当前方的数字是current_share和-next_share（这一方的-next_share是上一方的current_share的相反数），则实际的当前方的0分享是current_share-next_share

        """
        from crypten import generators

        tensor = ArithmeticSharedTensor(src=SENTINEL) # 初始化一个空的算术秘密分享的tensor
        if device is None:
            device = torch.device("cpu")
        elif isinstance(device, str):
            device = torch.device(device)
        g0 = generators["prev"][device] # 随机数发生器
        g1 = generators["next"][device]
        current_share = generate_random_ring_element(*size, generator=g0, device=device) # 生成随机数作为当
        next_share = generate_random_ring_element(*size, generator=g1, device=device)
        tensor.share = current_share - next_share # 生成当前方的0分享
        return tensor

...

    def reveal(self, dst=None):
        """Decrypts the tensor without any downscaling."""
        tensor = self.share.clone()
        if dst is None:
            return comm.get().all_reduce(tensor)
        else:
            return comm.get().reduce(tensor, dst)

    def get_plain_text(self, dst=None):
        """
        Decrypts the tensor.
        通过reduce操作将各方的share值收集起来然后求和得到编码后的原值x,之后解码
        """
        # Edge case where share becomes 0 sized (e.g. result of split)
        if self.nelement() < 1:
            return torch.empty(self.share.size())
        return self.encoder.decode(self.reveal(dst=dst))

class FixedPointEncoder:
    """Encoder that encodes long or float tensors into scaled integer tensors."""

    def __init__(self, precision_bits=None):
        """
        B=2^L
        x_encoded=round(Bx) -> type(long)
        x=x_encoded/B
        """
        if precision_bits is None:
            precision_bits = cfg.encoder.precision_bits
        self._precision_bits = precision_bits
        self._scale = int(2**precision_bits)

    def encode(self, x, device=None):
        """Helper function to wrap data if needed"""
        if isinstance(x, CrypTensor): # x是CrypTensor对象则直接return
            return x
        elif isinstance(x, int) or isinstance(x, float): # x是int或者float则将x*缩放因子，return对应的形状为(1,)的tensor
            # Squeeze in order to get a 0-dim tensor with value `x`
            return torch.tensor(
                [self._scale * x], dtype=torch.long, device=device
            ).squeeze()
        elif isinstance(x, list): # list 
            return (
                torch.tensor(x, dtype=torch.float, device=device)
                .mul_(self._scale)
                .long()
            )
        elif is_float_tensor(x): # float tensor
            return (self._scale * x).long()
        # For integer types cast to long prior to scaling to avoid overflow.
        elif is_int_tensor(x): # int tensor
            return self._scale * x.long()
        elif isinstance(x, np.ndarray): # numpy数组
            return self._scale * torch.from_numpy(x).long().to(device)
        elif torch.is_tensor(x): # 则如果是其他类型的torch tensor则error
            raise TypeError("Cannot encode input with dtype %s" % x.dtype)
        else: # 否则就是未知tensor error
            raise TypeError("Unknown tensor type: %s." % type(x))

    def decode(self, tensor):
        """Helper function that decodes from scaled tensor"""
        if tensor is None:
            return None
        assert is_int_tensor(tensor), "input must be a LongTensor"
        if self._scale > 1:
            correction = (tensor < 0).long()
            dividend = tensor.div(self._scale - correction, rounding_mode="floor")
            remainder = tensor % self._scale 
            remainder += (remainder == 0).long() * self._scale * correction

            tensor = dividend.float() + remainder.float() / self._scale
        else:
            tensor = nearest_integer_division(tensor, self._scale)

        return tensor.data

二、二进制秘密分享

可以看作是算术秘密分享的特殊情况，它是在二进制域 $Z /2 Z$ 中进行，用<x>表示一个值x的二进制秘密分享。相比于算术秘密分享，这里的运算都是mod 2下的，如加法为XOR，乘法为AND。
注意，XOR和AND运算构成了图灵完全运算集的基础（通过电路）。然而，每个顺序与门都需要一轮通信，这使得除了非常简单的电路之外的所有电路都非常低效，无法通过二进制秘密共享进行评估。在CRYPTEN中，只使用二进制秘密共享来实现比较器。
代码如下：

class BinarySharedTensor:
    """
    Encrypted tensor object that uses binary sharing to perform computations.

    Binary shares are computed by splitting each value of the input tensor
    into n separate random values that xor together to the input tensor value,
    where n is the number of parties present in the protocol (world_size).
    """

    def __init__(
        self, tensor=None, size=None, broadcast_size=False, src=0, device=None
    ):
        """
        Creates the shared tensor from the input `tensor` provided by party `src`.

        The other parties can specify a `tensor` or `size` to determine the size
        of the shared tensor object to create. In this case, all parties must
        specify the same (tensor) size to prevent the party's shares from varying
        in size, which leads to undefined behavior.

        Alternatively, the parties can set `broadcast_size` to `True` to have the
        `src` party broadcast the correct size. The parties who do not know the
        tensor size beforehand can provide an empty tensor as input. This is
        guaranteed to produce correct behavior but requires an additional
        communication round.

        The parties can also set the `precision` and `device` for their share of
        the tensor. If `device` is unspecified, it is set to `tensor.device`.
        """

        # do nothing if source is sentinel:
        if src == SENTINEL:
            return

        # assertions on inputs:
        assert (
            isinstance(src, int) and src >= 0 and src < comm.get().get_world_size()
        ), "specified source party does not exist"
        if self.rank == src:
            assert tensor is not None, "source must provide a data tensor"
            if hasattr(tensor, "src"):
                assert (
                    tensor.src == src
                ), "source of data tensor must match source of encryption"
        if not broadcast_size:
            assert (
                tensor is not None or size is not None
            ), "must specify tensor or size, or set broadcast_size"

        # if device is unspecified, try and get it from tensor:
        if device is None and tensor is not None and hasattr(tensor, "device"):
            device = tensor.device

        # assume zero bits of precision unless encoder is set outside of init:
        # 假设精度为0，除非编码器设置在init之外：
        self.encoder = FixedPointEncoder(precision_bits=0) 
        if tensor is not None:
            tensor = self.encoder.encode(tensor) # tensor*2^0
            tensor = tensor.to(device=device)
            size = tensor.size()

        # if other parties do not know tensor's size, broadcast the size:
        if broadcast_size:
            size = comm.get().broadcast_obj(size, src)

        # generate pseudo-random zero sharing (PRZS) and add source's tensor:
        self.share = BinarySharedTensor.PRZS(size, device=device).share
        if self.rank == src:
            self.share ^= tensor # 整体思路和算术秘密分享差不多，只是把+改成

    @staticmethod
    def PRZS(*size, device=None):
        """
        Generate a Pseudo-random Sharing of Zero (using arithmetic shares)

        This function does so by generating `n` numbers across `n` parties with
        each number being held by exactly 2 parties. Therefore, each party holds
        two numbers. A zero sharing is found by having each party xor their two
        numbers together.
        """
        from crypten import generators

        tensor = BinarySharedTensor(src=SENTINEL)
        if device is None:
            device = torch.device("cpu")
        elif isinstance(device, str):
            device = torch.device(device)
        g0 = generators["prev"][device]
        g1 = generators["next"][device]
        current_share = generate_kbit_random_tensor(*size, device=device, generator=g0)
        next_share = generate_kbit_random_tensor(*size, device=device, generator=g1)
        tensor.share = current_share ^ next_share
        return tensor        
       
    # 其他与算术秘密分享一致

三、秘密分享转换

1.A2B

为了从算术分享 $[x]$ 转换为二进制分享< $x$ >，各方首先秘密地与其他各方共享其算术分享，然后对所得分享进行加法运算。各方构造二进制秘密分享值< $y_p$ >，其中每个< $y_p$ >表示算术秘密分享之一，即 $y_p=[x]_p$ 。对于每一方 $p \in P$ 重复该过程，以创建所有|p|个算术共享 $x]_p$ 的二进制秘密分享。随后，各方计算< $x$ >= $_{p∈P}$ < $y_p$ >。为了计算和，可以使用进位先行加法器电路，在 $log_2(|P|)log_2(L)$ 的通信下。在实践中，进位先行加法器电路相当占用内存。当CRYPTEN耗尽GPU内存时，采用了一种替代的加法器电路，该电路需要更少的内存，但执行 $P|log_2(L)$ 通信轮次来执行求和。

2.B2A

为了从二进制共享< $x$ >转换为算术分享 $[x]$ ，各方计算 $[x]$ = $_{b=1}^B 2^b$ $x>^{(b)}]$ ，其中 $x^{(b)}>$ 表示二进制分享< $x$ >的第b位， B为分享秘密中的比特数。为了创建比特的算术分享，各方使用离线生成的b对秘密分享比特 $([r], < r >)$ 。这里， $[r]$ 和 < $r$ > 表示相同位的值 r 的算术和二进制秘密分享。然后使用如下算法从 $x >^{(b)}$ 生成 $x >^{(b)}]$ 。这个过程可以并行执行每个位，将转换过程所需的通信轮数减少到 1。
在这里插入图片描述

四、主要函数的实现

1.sigmoid

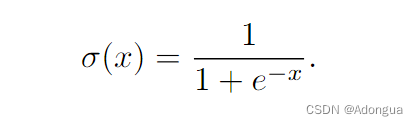
在这里插入图片描述

法1：切比雪夫近似

原理：
$\sigma([x]) = \frac{1}{2}tanh(\frac{[x]}{2}) + \frac{1}{2}$

代码实现：

    if method == "chebyshev":
        tanh_approx = tanh(self.div(2))
        return tanh_approx.div(2) + 0.5

法2：直接法

原理：
使用crypten定义的运算操作（指数exp、相反数neg、乘法mul、加法add、倒数reciprocal）计算原公式

代码实现：

elif method == "reciprocal":
        ltz = self._ltz()
        sign = 1 - 2 * ltz

        pos_input = self.mul(sign)
        denominator = pos_input.neg().exp().add(1)

        # TODO: Set these with configurable parameters
        with cfg.temp_override(
            {
                "functions.exp_iterations": 9,
                "functions.reciprocal_nr_iters": 3,
                "functions.reciprocal_all_pos": True,
                "functions.reciprocal_initial": 0.75,
            }
        ):
            pos_output = denominator.reciprocal()

        result = pos_output.where(1 - ltz, 1 - pos_output)
        # TODO: Support addition with different encoder scales
        # result = pos_output + ltz - 2 * pos_output * ltz
        return result

2.relu

原理：
$R e l u ([x]) = [x] [x > 0]$

代码实现：

def relu(self):
    """Compute a Rectified Linear function on the input tensor."""
    return self * self.ge(0) # 0,x<0 ;x,x>=0

3.tanh

法1：切比雪夫近似

原理：
$\sum_{j=1}^{terms} c_{2j - 1} P_{2j - 1} (x / maxval)$
其中 $c_i$ 是第i个切比雪夫级数系数， $P_i$ 是第i次多项式。近似值在[-1，1]外被截断为+/-1。

代码实现：

    elif method == "chebyshev":
        terms = cfg.functions.sigmoid_tanh_terms # default：32
        coeffs = crypten.common.util.chebyshev_series(torch.tanh, 1, terms)[1::2] # 切比雪夫级数
        tanh_polys = _chebyshev_polynomials(self, terms) # 计算输入为x的奇次切比雪夫多项式的值
        tanh_polys_flipped = (
            tanh_polys.unsqueeze(dim=-1).transpose(0, -1).squeeze(dim=0)
        )
        out = tanh_polys_flipped.matmul(coeffs) # 做矩阵乘法，等价于公式中的先乘积再求和

        # truncate outside [-maxval, maxval]
        return out.hardtanh()

法2：直接法

原理：
$2\sigma(2[x]) - 1$

代码实现：

    if method == "reciprocal":
        return self.mul(2).sigmoid().mul(2).sub(1)

4.exp

原理：
$\lim_{n \rightarrow \infty} (1 + \frac{[x]}{n})^n$
这里n=2^d，d是迭代次数

代码实现：

    iters = cfg.functions.exp_iterations # 看默认是8，则d=8

    result = 1 + self.div(2**iters) # 1+x/2^8
    # result^(2^8)
    for _ in range(iters):
        result = result.square() 
    return result

5.log

原理：
$h_n = 1 - x * exp(-y_n)$
$y_{n+1} = y_n - \sum_{k=1}^{order}\frac{h_n^k}{k}$
初始时， $y_0=\frac{x}{120}-20e^{-2x-1}+3$

代码实现：

    # Initialization to a decent estimate (found by qualitative inspection):
    #                ln(x) = x/120 - 20exp(-2x - 1.0) + 3.0
    iterations = cfg.functions.log_iterations # 2
    exp_iterations = cfg.functions.log_exp_iterations # 8
    order = cfg.functions.log_order # 8

    term1 = self.div(120)
    term2 = exp(self.mul(2).add(1.0).neg()).mul(20)
    y = term1 - term2 + 3.0 

    # 8th order Householder iterations
    with cfg.temp_override({"functions.exp_iterations": exp_iterations}):
        for _ in range(iterations):
            h = 1 - self * exp(-y)
            y -= h.polynomial([1 / (i + 1) for i in range(order)]) # 按公式迭代计算8次
    return y

6.reciprocal

法1：NR迭代法

原理：
$y_{i+1} = (2y_i -x * y_i^2)$
初始时， $y_0=3*exp(1 - 2x) + 0.003$

代码实现：

    if method == "NR":
        nr_iters = cfg.functions.reciprocal_nr_iters
        if initial is None:
            # Initialization to a decent estimate (found by qualitative inspection):
            #                1/x = 3exp(1 - 2x) + 0.003
            result = 3 * (1 - 2 * self).exp() + 0.003
        else:
            result = initial
        for _ in range(nr_iters):
            if hasattr(result, "square"):
                result += result - result.square().mul_(self)
            else:
                result = 2 * result - result * result * self
        return result

法2：直接法

原理：
$x^{-1} = exp(-log(x))$

代码实现：

    elif method == "log":
        log_iters = cfg.functions.reciprocal_log_iters
        with cfg.temp_override({"functions.log_iters": log_iters}):
            return exp(-log(self))

7.cos与sin

原理：
根据欧拉公式，
$sinx=Im(e^{ix})=\frac{(e^{ix}-e^{-ix})}{2i}$
$cosx=Re(e^{ix})=\frac{(e^{ix}+e^{-ix})}{2}$
使用重复平方方法来有效地计算复杂的指数，从而能够计算正弦函数和余弦函数。

代码实现：

def _eix(self):
    r"""Computes e^(i * self) where i is the imaginary unit.
    Returns (Re{e^(i * self)}, Im{e^(i * self)} = cos(self), sin(self)
    """
    iterations = cfg.functions.trig_iterations

    re = 1
    im = self.div(2**iterations)

    # First iteration uses knowledge that `re` is public and = 1
    re -= im.square()
    im *= 2

    # Compute (a + bi)^2 -> (a^2 - b^2) + (2ab)i `iterations` times
    for _ in range(iterations - 1):
        a2 = re.square()
        b2 = im.square()
        im = im.mul_(re)
        im._tensor *= 2
        re = a2 - b2

    return re, im

def cossin(self):
    r"""Computes cosine and sine of input via exp(i * x).

    Args:
        iterations (int): for approximating exp(i * x)
    """
    return self._eix()

def cos(self):
    r"""Computes the cosine of the input using cos(x) = Re{exp(i * x)}

    Args:
        iterations (int): for approximating exp(i * x)
    """
    return cossin(self)[0]

def sin(self):
    r"""Computes the sine of the input using sin(x) = Im{exp(i * x)}

    Args:
        iterations (int): for approximating exp(i * x)
    """
    return cossin(self)[1]

8.比较运算

原理：
为了比较两个秘密共享值 [x] 和 [y]，我们可以通过计算它们的差异 [z] = [x] - [y] 并将结果与零进行比较，即去计算[z<0]：首先将[z]转换为二进制秘密分享<z>，将<z>右移L-1位，得到符号位<b>，之后将该结果转化位算术秘密分享[b]。
因为我们使用整数编码，所以 z 的最高位代表它的符号。可以直接使用小于电路来判断[x < y]，但这需要将额外的值转换为二进制秘密分享，并产生另一个 $log_2L$ 轮的通信来计算小于电路，所以不采用。
在有了[x<y]的判别函数之后，我们可以直接利用该判别函数来得到其他比较器：
在这里插入图片描述
代码实现：

    # Comparators
    def _ltz(self):
        """Returns 1 for elements that are < 0 and 0 otherwise"""
        shift = torch.iinfo(torch.long).bits - 1 # L-1
        precision = 0 if self.encoder.scale == 1 else None

        result = self._to_ptype(Ptype.binary) # 将MPCSensor的基础共享转换为相应的ptype，这里是将算术秘密分享转换为二进制秘密分享（[z] -> <z>）
        result.share >>= shift # <b> = <z> >> (L-1)
        result = result._to_ptype(Ptype.arithmetic, precision=precision, bits=1) # <b> -> [b]
        result.encoder._scale = 1
        return result

def lt(self, y):
    """Returns self < y"""
    return (self - y)._ltz() # [x<y] <=> [x-y<0]

def ge(self, y):
    """Returns self >= y"""
    return 1 - self.lt(y) # 1-[x<y]

def gt(self, y):
    """Returns self > y"""
    return (-self + y)._ltz() # [y<x] <=> [-x+y<0]

def le(self, y):
    """Returns self <= y"""
    return 1 - self.gt(y) # 1-[y<x]

def ne(self, y):
    """Returns self != y"""
    difference = self - y # x-y，相等则为0
    difference = type(difference).stack([difference, -difference]) # 将差值张量和它的相反数张量在同一个张量中进行排列
    return difference._ltz().sum(0) # 利用_ltz()方法判断difference张量中的元素是否小于零，返回一个布尔类型的张量。然后使用sum(0)对每一列（或者说沿着0维）进行求和操作，最终得到每列中小于零的元素个数，这个结果即为不相等的情况个数

def eq(self, y):
    """Returns self == y"""
    return 1 - self.ne(y) # 1-[x!=y]

9.max_pool2d

①argmax

得到最大值元素的索引信息

法1：成对比较（The pairwise）

原理：
对于长度为R的序列 $a_1,a_2,...,a_R)$ ，生成一个R*R的差异矩阵A，其中 $A_{1j}=(a_1-a_1,a_1-a_2,...,a_1-a_R)$ ，i从1到R依此类推。之后做[A>=0]运算，若某行结果结果全部大于等于0，则该行对应的元素即为最大值。

代码实现：

def _argmax_helper_pairwise(enc_tensor, dim=None):
    """Returns 1 for all elements that have the highest value in the appropriate
    dimension of the tensor. Uses O(n^2) comparisons and a constant number of
    rounds of communication

    - enc_tensor：要查找最大值的输入张量。
    - dim：指定要在其上查找最大值的维度，默认为 None，表示在整个张量上查找
    """
    dim = -1 if dim is None else dim
    row_length = enc_tensor.size(dim) if enc_tensor.size(dim) > 1 else 2 # 根据输入张量的维度大小计算行长度

    # Copy each row (length - 1) times to compare to each other row
    a = enc_tensor.expand(row_length - 1, *enc_tensor.size())  # 此时每个元素将有r个

    # Generate cyclic permutations for each row
    b = crypten.stack([enc_tensor.roll(i + 1, dims=dim) for i in range(row_length - 1)]) # 相当于生成r个那个维度所有元素组成的序列

    # Use either prod or sum & comparison depending on size（乘积或求和比较）
    if row_length - 1 < torch.iinfo(torch.long).bits * 2:
        pairwise_comparisons = a.ge(b) # a>=b，若结果序列每个元素都为1，则乘积就是1，否则为0，那个序列对应的元素就是最大值
        result = pairwise_comparisons.prod(0) # 返回给定维度“dim”中“input”张量每行的乘积
    else:
        # Sum of columns with all 1s will have value equal to (length - 1).
        # Using ge() since it is slightly faster than eq()
        pairwise_comparisons = a.ge(b)
        result = pairwise_comparisons.sum(0).ge(row_length - 1) # 采用求和的话就是，当1的个数是大于等于r-1，则是最大元素
    return result, None

计算效率较低，但是通信开销小。 $O (1)$ 轮通信， $O(N^2)$ 通信位， $O(N^2)$ 计算复杂度

法2：树归约（The tree-reduction）

原理：
树归约算法通过将输入分成两半来计算 argmax，然后比较每半的元素。这在每一轮中将输入的大小减少了一半，需要 $O(log_2 N )$ 轮来完成 argmax。

代码实现：

def _compute_pairwise_comparisons_for_steps(input_tensor, dim, steps):
    """
    Helper function that does pairwise comparisons by splitting input
    tensor for `steps` number of steps along dimension `dim`.
    """
    enc_tensor_reduced = input_tensor.clone()
    for _ in range(steps):
        m = enc_tensor_reduced.size(dim)
        x, y, remainder = enc_tensor_reduced.split([m // 2, m // 2, m % 2], dim=dim)
        pairwise_max = crypten.where(x >= y, x, y)
        enc_tensor_reduced = crypten.cat([pairwise_max, remainder], dim=dim)
    return enc_tensor_reduced

def _max_helper_log_reduction(enc_tensor, dim=None):
    """Returns max along dim `dim` using the log_reduction algorithm"""
    if enc_tensor.dim() == 0:
        return enc_tensor
    input, dim_used = enc_tensor, dim
    if dim is None:
        dim_used = 0
        input = enc_tensor.flatten()
    n = input.size(dim_used)  # number of items in the dimension
    steps = int(math.log(n))
    enc_tensor_reduced = _compute_pairwise_comparisons_for_steps(input, dim_used, steps)

    # compute max over the resulting reduced tensor with n^2 algorithm
    # note that the resulting one-hot vector we get here finds maxes only
    # over the reduced vector in enc_tensor_reduced, so we won't use it
    with cfg.temp_override({"functions.max_method": "pairwise"}):
        enc_max_vec, enc_one_hot_reduced = enc_tensor_reduced.max(dim=dim_used)
    return enc_max_vec

def _max_helper_all_tree_reductions(enc_tensor, dim=None, method="log_reduction"):
    """
    Finds the max along `dim` using the specified reduction method. `method`
    can be one of [`log_reduction`, `double_log_reduction`, 'accelerated_cascade`]
    `log_reduction`: Uses O(n) comparisons and O(log n) rounds of communication
    `double_log_reduction`: Uses O(n loglog n) comparisons and O(loglog n) rounds
    of communication (Section 2.6.2 in https://folk.idi.ntnu.no/mlh/algkon/jaja.pdf)
    `accelerated_cascade`: Uses O(n) comparisons and O(loglog n) rounds of
    communication. (See Section 2.6.3 of https://folk.idi.ntnu.no/mlh/algkon/jaja.pdf)
    """
    if method == "log_reduction":
        return _max_helper_log_reduction(enc_tensor, dim)
    elif method == "double_log_reduction":
        return _max_helper_double_log_reduction(enc_tensor, dim)
    elif method == "accelerated_cascade":
        return _max_helper_accelerated_cascade(enc_tensor, dim)
    else:
        raise RuntimeError("Unknown max method")

def _argmax_helper_all_tree_reductions(enc_tensor, dim=None, method="log_reduction"):
    """
    Returns 1 for all elements that have the highest value in the appropriate
    dimension of the tensor. `method` can be one of [`log_reduction`,
    `double_log_reduction`, `accelerated_cascade`].
    `log_reduction`: Uses O(n) comparisons and O(log n) rounds of communication
    `double_log_reduction`: Uses O(n loglog n) comparisons and O(loglog n) rounds
    of communication 
    """
    enc_max_vec = _max_helper_all_tree_reductions(enc_tensor, dim=dim, method=method)
    # reshape back to the original size
    enc_max_vec_orig = enc_max_vec
    if dim is not None:
        enc_max_vec_orig = enc_max_vec.unsqueeze(dim)
    # compute the one-hot vector over the entire tensor
    enc_one_hot_vec = enc_tensor.eq(enc_max_vec_orig)
    return enc_one_hot_vec, enc_max_vec

计算效率较高，但是通信开销大。 $O(log_2 N )$ 轮通信， $O(N^2)$ 通信位， $O (N)$ 计算复杂度

②maximum

原理：
基本思路就是通过树归约或成对比较来得到记录了最大元素的onehot编码，之后将tensor和onehot相乘，onehot中唯一是1的那个元素会保留，其他都会抹0，之后求和即可得到最大值。

代码实现：

def max(self, dim=None, keepdim=False, one_hot=True):
    """
    Returns the maximum value of all elements in the input tensor.
    基本思路就是通过树归约或成对比较来得到记录了最大元素的onehot编码，之后将tensor和onehot相乘，onehot中唯一是1的那个元素会保留，
    其他都会抹0，之后求和即可得到最大值
    """
    method = cfg.functions.max_method
    if dim is None:
        if method in ["log_reduction", "double_log_reduction"]:
            # max_result can be obtained directly
            max_result = _max_helper_all_tree_reductions(self, method=method)
        else:
            # max_result needs to be obtained through argmax
            with cfg.temp_override({"functions.max_method": method}):
                argmax_result = self.argmax(one_hot=True)
            max_result = self.mul(argmax_result).sum()
        return max_result
    else:
        argmax_result, max_result = _argmax_helper(
            self, dim=dim, one_hot=True, method=method, _return_max=True
        )
        if max_result is None:
            max_result = (self * argmax_result).sum(dim=dim, keepdim=keepdim)
        if keepdim:
            max_result = (
                max_result.unsqueeze(dim)
                if max_result.dim() < self.dim()
                else max_result
            )
        if one_hot:
            return max_result, argmax_result
        else:
            return (
                max_result,
                _one_hot_to_index(argmax_result, dim, keepdim, self.device),
            )

③池化运算

代码实现：

def max_pool2d(
    self,
    kernel_size,
    padding=0,
    stride=None,
    dilation=1,
    ceil_mode=False,
    return_indices=False,
):
    """Applies a 2D max pooling over an input signal composed of several
    input planes.
    """
    max_input = self.clone() # 创建副本
    max_input.data, output_size = _pool2d_reshape(
        self.data,
        kernel_size,
        padding=padding,
        stride=stride,
        dilation=dilation,
        ceil_mode=ceil_mode,
        # padding with extremely negative values to avoid choosing pads.
        # The magnitude of this value should not be too large because
        # multiplication can otherwise fail.
        pad_value=(-(2**24)),
        # TODO: Find a better solution for padding with max_pooling
    ) # 形状重塑：Rearrange a 4-d tensor so that each kernel is represented by each row
    max_vals, argmax_vals = max_input.max(dim=-1, one_hot=True) # 求每个窗口中的最大值和索引
    max_vals = max_vals.view(output_size) # 将最大值结果重新调整为输出尺寸
    if return_indices:
        if isinstance(kernel_size, int):
            kernel_size = (kernel_size, kernel_size)
        argmax_vals = argmax_vals.view(output_size + kernel_size)
        return max_vals, argmax_vals
    return max_vals

求最小，其实就是求最大的相反的操作，只要对[-x]求最大即可

10.四则运算

①加法/减法

另一个操作数为明文：

[x]+c = (x1+c,x2,…,xn)

另一个操作数为密文：

[x]+[y]=(x1+y1,x2+y2,…,xn+yn)

add操作涉及到了匹配字符串op，判断是否是add运算；对输入进行编码；类型判断等操作，因此运算的时间还是会差了pytorch大概3个数量级，并由于编码所以存在一定误差

②乘法相关运算

另一个操作数为明文：

[cx] = (cx1,cx2,…,cxn)

另一个操作数为密文：

基于Beaver三元组(a,b,c)，其中c=ab，由TTP生成

$[\epsilon]=[x]-[a]$ ， $[\delta]=[y]-[b]$

则 $[x][y]=[c]+\epsilon[b]+[a]\delta+\epsilon\delta$

代码实现如下：

def __beaver_protocol(op, x, y, *args, **kwargs):
    """Performs Beaver protocol for additively secret-shared tensors x and y

    1. Obtain uniformly random sharings [a],[b] and [c] = [a * b]
    2. Additively hide [x] and [y] with appropriately sized [a] and [b]
    3. Open ([epsilon] = [x] - [a]) and ([delta] = [y] - [b])
    4. Return [z] = [c] + (epsilon * [b]) + ([a] * delta) + (epsilon * delta)
    """
    assert op in {
        "mul",
        "matmul",
        "conv1d",
        "conv2d",
        "conv_transpose1d",
        "conv_transpose2d",
    }
    if x.device != y.device:
        raise ValueError(f"x lives on device {x.device} but y on device {y.device}")

    provider = crypten.mpc.get_default_provider()
    a, b, c = provider.generate_additive_triple(
        x.size(), y.size(), op, device=x.device, *args, **kwargs
    ) # a，b，c由可信赖的第三方（TTP）提供

    from .arithmetic import ArithmeticSharedTensor

    if cfg.mpc.active_security:
        """
        Reference: "Multiparty Computation from Somewhat Homomorphic Encryption"
        Link: https://eprint.iacr.org/2011/535.pdf
        """
        f, g, h = provider.generate_additive_triple(
            x.size(), y.size(), op, device=x.device, *args, **kwargs
        )

        t = ArithmeticSharedTensor.PRSS(a.size(), device=x.device)
        t_plain_text = t.get_plain_text()

        rho = (t_plain_text * a - f).get_plain_text()
        sigma = (b - g).get_plain_text()
        triples_check = t_plain_text * c - h - sigma * f - rho * g - rho * sigma
        triples_check = triples_check.get_plain_text()

        if torch.any(triples_check != 0):
            raise ValueError("Beaver Triples verification failed!")

    # Vectorized reveal to reduce rounds of communication
    with IgnoreEncodings([a, b, x, y]):
        epsilon, delta = ArithmeticSharedTensor.reveal_batch([x - a, y - b])

    # z = c + (a * delta) + (epsilon * b) + epsilon * delta
    c._tensor += getattr(torch, op)(epsilon, b._tensor, *args, **kwargs)
    c._tensor += getattr(torch, op)(a._tensor, delta, *args, **kwargs)
    c += getattr(torch, op)(epsilon, delta, *args, **kwargs)

    return c

其他主要函数，例如mean、neg、matmul、conv、avg_pool、dropout等也都是依赖于这些基本的运算，然后套公式、基本的原理得到的

附录

函数	函数名	描述
绝对值	abs	将值乘以其符号
加法	add、+	每一方都会增加各自的分享值
最大参数	argmax	执行成对比较或者树归约
最小参数	argmin	执行成对比较或者树归约
平均池化	avg_pool2d	各方计算其分享值的平均池化
批量规范化	batchnorm	使用求和、除法和方差函数对值进行批量规范化
二进制与	and、&	使用二进制Beaver协议进行计算
二进制交叉熵	binary_cross_entropy	使用对数、乘法和加法函数进行计算
二进制异或	xor、^	每一方对各自的分享值做异或运算
克隆	clone	每一方都克隆自己的分享值
比较	>=, <=, =, ge, le, eq	去和0比较，转换为二进制秘密分享并检查其最高有效位，即符号位
拼接	cat	各方将各自的分享值拼接起来
卷积	conv1d, conv2d	若过滤器是公共的，则每一方都对其分享值进行卷积。如果过滤器是私有的，则使用Beaver协议进行计算。
余弦	cos	使用重复平方法近似
交叉熵	cross_entropy	使用softmax、对数、乘法和除法函数进行计算
累计和	cumsum	各方计算其分享值的累计价值总和
除法	div、/	如果除数是公共的，将分享值除以该除数并更正环绕错误
点积	dot	按元素乘，并求和结果
Dropout	dropout	Dropout掩码不加密
错误函数	erf	使用麦克劳林级数近似
指数	exp	近似使用极限近似
展平	flatten	每一方都展平他们的分享值
翻转	flip	每一方都翻转他们的分享值
截断正切	hardtanh	使用比较、乘法和加法函数进行计算
对数	log	使用高阶修正豪斯霍尔德方法进行近似
对数-softmax	log_softmax	使用幂函数、最大值函数、求和函数和加法函数进行计算
矩阵乘法	matmul	如果一个矩阵是公共矩阵，则各方矩阵乘以其分享值。如果两个矩阵都是私有的，使用Beaver协议进行计算
最大值求解	max	先做argmax得到含有最大值信息的one-hot编码，之后和输入计算点积
最大池化	max_pool2d	计算最大值
均值	mean	各方计算各自分享值的平均值
最小值求解	min	先做argmin得到含有最小值信息的one-hot编码，之后和输入计算点积
乘积	mul、*	如果乘数是公共的，则各方将其分享值乘以乘数。如果乘数是私有的，则使用Beaver协议
多路复用	where	将第一个值乘以二进制掩码；将第二个值乘以反向掩码
取反	neg	每一方将其分享值取反
规范化	norm	使用平方、和与平方根函数进行计算
外积	ger	执行每对元素的乘法运算
填充	pad	每一方将分享值进行填充操作
排列	permute	每一方排列他们的分享值。索引不加密
元素积	prod	将输入中的所有元素相乘
乘方	pow、pos_pow	对于正幂，对数域和指数相乘。对于负幂，计算倒数并评估正幂
倒数	reciprocal	使用牛顿迭代法迭代近似
ReLU	relu、relu6	将值与0进行比较，并将值乘以得到的掩码
形状调整	reshape, view	每一方重塑他们的分享值
沿着给定的维度滚动张量	roll	每一方都滚动他们的分享值
返回根据index映射关系映射后的新张量	scatter	每一方将一个分享分散到另一个分享中。索引不加密。
选择	gather、index_select、narrow、take	每一方选择他们的部分分享值。索引不加密
Sigmoid	sigmoid	使用指数函数和倒数函数计算
符号函数	sign	将值与 0 进行比较，乘以 2，减去 1。
正弦	sin	使用重复平方方法近似
Softmax	softmax	使用求幂、最大值、求和与倒数函数计算
平方	square	Beaver协议计算
开平方	sqrt	使用牛顿迭代法迭代近似
Squeezing	squeeze	每一方从其分享值中删除大小为 1 的维度
堆叠	stack	每一方堆叠他们的分享值
减法	sub、-	每一方减去他们的分享值
求和	sum	每一方对其分享中的所有值求和
正切	tanh	对输出的 sigmoid 值进行线性变换
求迹	trace	每一方对其分享值的所有对角元素求和
转置	t, transpose	每一方都转置他们的分享值。
Unsqueezing	unsqueeze	每一方在其分享中添加大小为 1 的维度
方差	var	使用平方、加法和减法函数计算