数学建模笔记（八）：微分方程的应用（偏微分方程）

已于 2022-07-12 11:02:41 修改
阅读量8.2k 收藏 113
点赞数 18
分类专栏： 数学建模笔记 文章标签： 算法 数学建模 微分方程
于 2022-07-06 21:40:47 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_52441682/article/details/125631705
版权

文章目录

一、微分方程概述

1.什么是微分方程

在这里插入图片描述

2.求解方法

（一）求精确解

计算出来

（二）求数值解（近似解）

用数学软件可以模拟出来

（三）定性理论方法

分析解的情况，满足何种性态
在这里插入图片描述

3.建立微分模型的方法

（一）根据定理规律列方程

（二）微元分析法

（三）模拟近似法

在这里插入图片描述
在这里插入图片描述

4.适用问题

在这里插入图片描述

5.常见动态模型

在这里插入图片描述

二、观众厅地面设计

1.问题背景

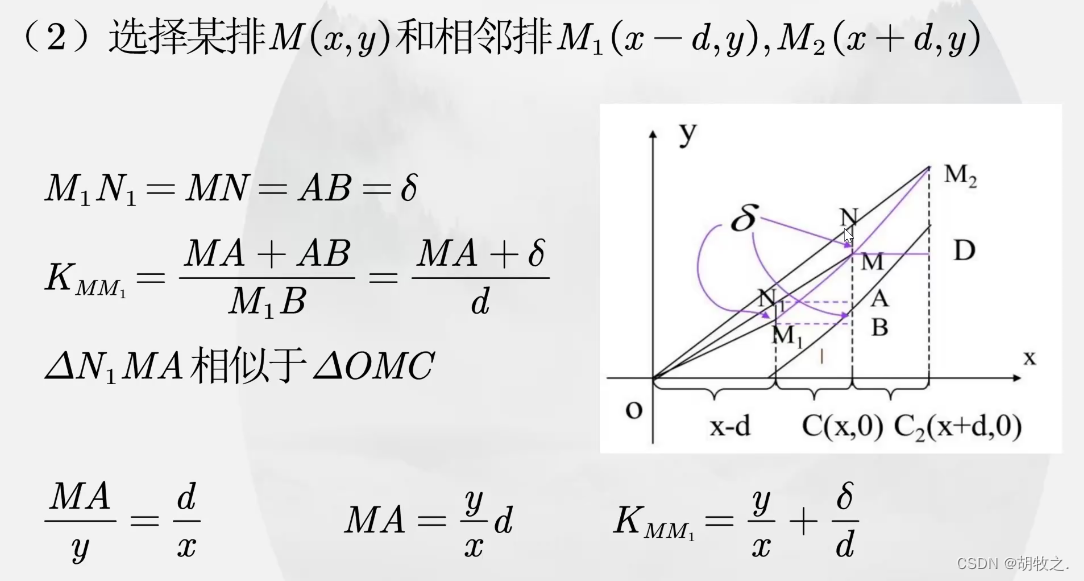
在这里插入图片描述

2.模型假设

在这里插入图片描述

3.模型建立

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

4.模型求解

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

5.总结与讨论

在这里插入图片描述

三、古尸年代鉴定问题

1.问题背景

在这里插入图片描述

2.建模求解

在这里插入图片描述

3.模型修正

在这里插入图片描述

四、正规战和游击战模型

1.问题背景

在这里插入图片描述
在这里插入图片描述

2.模型假设

在这里插入图片描述

3.模型建立与求解

双方采取相同战略时
在这里插入图片描述
由k值判断情况
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
混合战斗时
在这里插入图片描述

五、万有引力定律的发现

1.问题背景

在这里插入图片描述

2.模型建立与求解

在这里插入图片描述

在这里插入图片描述

六、偏微分方程概述

1.概述

在这里插入图片描述

2.简单一阶偏微分方程求解

在这里插入图片描述

七、交通流

1.问题背景

在这里插入图片描述
在这里插入图片描述

2.模型假设

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

八、二阶偏微分方程

1.一般形式（根据 d e l t a delta delta区分的三类偏微分方程）

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

2.弦振动方程模型（双曲型偏微分方程）

（一）介绍

在这里插入图片描述
在这里插入图片描述

（二）例子——斜拉桥的钢索问题

在这里插入图片描述

3.热传导方程模型（抛物型方程）

（一）介绍

在这里插入图片描述
在这里插入图片描述

（二）例子——不同深度的溶氧浓度

4.调和方程模型（椭圆型方程）

（一）介绍

在这里插入图片描述

（二）例子——生物体内各点的电位

在这里插入图片描述

九、烟雾的扩散与消失（二阶偏微分方程）

1.问题背景

在这里插入图片描述

2.问题分析

在这里插入图片描述

在这里插入图片描述

3.模型假设与建立

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

4.结果计算

在这里插入图片描述

5.结果分析

在这里插入图片描述

数学建模--微分方程
🌟【AI炼丹师 | 你的数字技术搭子】 大二解锁3200+道友同行👾
07-30 1759
在数学建模中，微分方程模型是一种极其重要的方法，广泛应用于各种实际问题的描述和解决。微分方程模型通过建立变量及其变化率之间的关系，可以预测和分析系统的行为。这些模型在科技、工程、生态、环境、人口、交通、医学、经济管理等各个领域都有广泛应用。
数学建模进阶：偏微分方程与实战解析
m0_52343631的博客
06-12 739
在物理学、生物学、工程学等各种科学领域中，偏微分方程（Partial Differential Equations, PDEs）作为一个强大的工具，经常被用于描述各种复杂的现象。要深入理解并应用偏微分方程，需要对其原理有深入的理解，并且需要对其求解技术有一定的掌握。在本文中，我们将详细讲解偏微分方程的原理，常见类型及其物理意义，解析方法和数值方法，并且配合实际案例，给出MATLAB代码进行演示。希望这篇文章能帮助你在数学建模的道路上迈出坚实的一步。在理解偏微分方程之前，我们需要先了解一下微分方程的基本概念。
数学建模——常偏微分方程模型（上）（模型详解和matlab代码）
热门推荐
z828849eser的博客
02-17 1万+
1.人口增长 马尔萨斯模型 模型假设 (i)设x(t)表示t时刻的人口数，且x(t)连续可微 (ii)人口额度增长率r是常数（增长率=出胜率-死亡率） (iii)人口数量的变化是封闭的，即人口数量的增加和减少只取决于人口中个体的生育和死亡，且每一个体都具有同样的生育能力和死亡率 建模和求解 于是得 解得       阻滞增长模型（Logistic模型） 模...
偏微分方程：理论、应用与计算方法
最新发布
weixin_42527589的博客
03-15 1761
偏微分方程（Partial Differential Equations，简称PDE）是数学中用于描述物理现象中各种场的演变规律的一种数学模型。它的解通常依赖于多个独立变量（例如时间和空间坐标），是现代科学与工程领域不可或缺的工具，从气候模型到金融风险分析，再到材料科学的模拟，偏微分方程都在其中扮演了关键角色。偏微分方程（Partial Differential Equation，简称PDE）是含有未知多变量函数及其偏导数的方程。
谈谈偏微分方程在图像特效中的应用
weixin_33882452的博客
03-26 224
在很早之前，iOS上有这样一款软件叫Pimple Eraser,它实现的功能非常简单，就是把人脸中的痘痘给去掉，而且效果很不错。当然你得手动的选择痘痘的位置和大小。不过可惜的是，这款软件的交互做的不是很好。大约一年之后，美图秀秀新的版本也实现了同样的功能，而且它的人机交互功能做得比Pimple Eraser好的多，由此成为美图秀秀新的亮点。与此类似，百度魔图其实早就有这一功能，不过...
【数学建模笔记 20】数学建模的偏微分方程的数值解
Koorye今天自学了吗
07-28 1646
20. 偏微分方程的数值解 定解问题 各种物理性质的定常过程都可用椭圆型方程描述 Δu=∂2u∂x2+∂2u∂y2=f(x,y), \Delta u=\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}=f(x,y), Δu=∂x2∂2u​+∂y2∂2u​=f(x,y), 当 f(x,y)=0f(x,y)=0f(x,y)=0 时，即拉普拉斯方程 Δu=∂2u∂x2+∂2u∂y2=0. \Delta u=\frac{\partial
数学建模学习笔记——微分方程建模
m0_65079623的博客
03-21 541
本文章为《数学建模算法与应用（司守奎）》书籍的学习笔记，文章内代码大部分为该书籍的搬运或在网络上的搜集，主要目的为简化阅读的过程，以便直接实现代码的运用，我也会对书中的习题给出自己的解。
数学建模之微分方程学习笔记
rrrrroin的博客
07-27 1153
数学建模之微分方程经典模型
【考研数学】第三章：微分方程（复习版）
m0_68863842的博客
05-22 2238
​​​​​​​做题优先考虑通过四则运算把y'前面的系数变为1，如果观察不出是什么形式的话，可以考虑把dx当作分子，dy当作分母，把y'=dy/dx变为dx/dy形式观察，此时的dx就要当因变量来看待dy当自变量来看待了（如果不理解可以换元，x换元成y，y换元成x，来观察是什么形式的微分方程），而且都简单，最多到2阶导数，如果试着去理解或者用其他人的方法可能会很浪费时间和效率，这里引用了b站一位up主的笔记，写的很好，直接看就行。Qm(x)多项式根据原等式右边的多项式构造相应的待定系数，Qm(x)可以。
Evans偏微分方程四大方程_49
06-29
1. **基础知识**：偏微分方程的定义、分类及其物理意义。 2. **解的存在性与唯一性**：对于特定类型的偏微分方程，探讨其解的存在性和唯一性条件。 3. **解的性质**：分析解的连续性、光滑性等性质。 4. **数值解法*...
一份较为详细的《常微分方程》笔记
08-03
《常微分方程》是一门研究物体动态行为和系统演变的重要数学学科，这份194页的学习笔记全面概述了该领域的基础知识和求解方法。笔记由Gabriel Nagy撰写，来自密歇根州立大学数学系，内容涵盖了一阶和二阶常微分方程...
数学建模讲义:微分方程模型
08-25
微分方程模型的数学建模讲义，包含人口预报问题,传染病问题,作战模型,捕食问题,火箭发射问题等
微分方程及应用
01-15
微分方程模型，及相关应用技术
有关微分方程建模的几个实例
10-30
有关微分方程建模的几个实例如：嫌疑犯问题，含盐量问题，导弹追踪问题， 悬链线方程问题，放射性核废料处理问题
[偏微分方程讲义].(俄罗斯)奥列尼克.清晰版
02-28
[偏微分方程讲义].(俄罗斯)奥列尼克.清晰版
二维热传导偏微分方程求解
12-07
自己编写的二维传热的偏微分方程中心差分方法离散求解程序
微分方程模型——偏微分方程
hanhan的博客
07-14 8706
1. 简介 微分方程：描述自然界中存在的物理现象和普遍规律。 常微分方程（ODE） 偏微分方程（PDE） 偏微分方程理论： 物理/工程问题————翻译（建模）/物理工程规律————》数学问题（PDE） 物理/工程问题————求解/数学理论————》数学结果 物理/工程问题————分析————》数学公式/物理意义 偏微分方程的基本概念： 定义：未知函数及其偏导数所满足的方程；F(x, u(x), Du, D2u,…, Dnu) = 0; 阶数：偏微分方程中偏导数的最高阶数，有n阶就为n。 线性偏微分
【数学建模】微分方程模型
2401_82622411的博客
01-30 2563
6）options（可选）：options=odeset('reltol','rt','abstol',at)，rt，at分别为设定的相对误差，默认为10e-3，10e-6。取x1(0)=25,x2(0)=2,战前e=0.3，战后e=0.1，r1=1,r2=0.02,λ1=0.1,λ2=0.02。SIS模型考虑了病人被治愈的情况，未考虑被治愈的病人产生抗体，不会再次感染，即不参与循环的情况。2）字母D表示微分，D2表示二阶微分，D3表示三阶微分，后面跟要求解的因变量（Dy）i)建立m文件，编辑f函数。
偏微分方程的数值解(三): 化工应用实例 ----------触煤反应装置内温度及转换率的分布
冷月无声的博客
05-01 5762
偏微分方程的数值解系列博文： 偏微分方程的数值解(一):定解问题 & 差分解法 偏微分方程的数值解(二): 一维状态空间的偏微分方程的 MATLAB 解法 偏微分方程的数值解(三): 化工应用实例 ----------触煤反应装置内温度及转换率的分布 偏微分方程的数值解(四): 化工应用————扩散系统之浓度分布 偏微分方程的数值解(五)： 二维状态空间的偏微分方程的 MATLA...
柱坐标下NO浓度模型的偏微分方程模拟及其应用
值得注意的是，本文提及了与传统数学模型相比，空间和运动的整合在形式主义建模中的重要性，以及不同数学技术如普通微分方程（ODE）、连续时间马尔可夫链（CTMC）的应用。此外，空间可以采用几何或拓扑的方式表示，...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值