IMATEST-Color Correction Matrix阅读笔记（一）

ikun的男人

于 2025-04-07 10:27:10 发布

阅读量659

点赞数 15

分类专栏： IMATEST 文章标签：笔记

本文链接：https://blog.csdn.net/qq_52538756/article/details/146979918

版权

IMATEST 专栏收录该内容

4 篇文章

订阅专栏

免责声明：本文所提供的信息和内容仅供参考。作者对本文内容的准确性、完整性、及时性或适用性不作任何明示或暗示的保证。在任何情况下，作者不对因使用本文内容而导致的任何直接或间接损失承担责任，包括但不限于数据丢失、业务中断或其他经济损失。

读者在使用本文信息时，应自行验证其准确性和适用性，并对其使用结果负责。本文内容不构成专业技术咨询或建议，具体的技术实现和应用应根据实际情况和需要进行详细分析和验证。

本文所涉及的任何商标、版权或其他知识产权均属于其各自的所有者。若本文中引用了第三方的资料或信息，引用仅为学术交流目的，不构成对第三方内容的认可或保证。

若有任何疑问或需进一步信息，请联系本文作者或相关专业人士。

前言

小编最近在学习ISP的相关知识，想研究算法并部署到MPSOC上，今天跟着小编一起学习IMATEST的Color Correction Matrix文档吧。

一、Introduction

CCM 计算

计算CCM需要至少9个不同颜色的色块，但通常使用24色块的X-Rite ColorChecker色卡。
3×3 CCM（推荐）和 4×3 CCM 是不同的矩阵计算方法：
- 3×3 CCM: 只考虑颜色通道（R, G, B）之间的线性关系，通常用于色彩校正。
- 4×3 CCM: 额外考虑偏移项（偏移量用于处理零点漂移）。
计算CCM的方法是最小均方误差（MSE, Mean Squared Error），目标是让校正后的色块与标准参考值的色差最小。

颜色误差计算

误差默认是使用ΔE 2000 或 ΔE 94（这两种计算方式类似）。
计算时：
- 只考虑亮度在 5 ≤ L ≤ 98 之间的色块（避免极暗或极亮区域）。
- 只考虑RGB通道未达到饱和的色块（RGB < 99%）。

线性化（Linearization）

CCM 计算要求输入的 R, G, B 值是线性的，否则矩阵计算会出现偏差。
为什么需要线性化？
- 许多图像格式（如sRGB、JPEG）默认使用了伽马校正（非线性）。
- 在计算CCM之前，必须去除伽马影响，使RGB值回归线性，以保证矩阵变换正确。

二、Sequence of operations — The Flow chart

流程大致如下：

读取RGB图像（建议使用RAW图像，以避免预处理影响）。
观察伽马曲线，选择适当的线性化设置。
选择CCM设置，包括优化模式、线性化选项等，同时指定目标色彩空间和参考文件。
运行优化器：
- 以初始矩阵开始（通常为单位矩阵）。
- 计算校正后的RGB值或XYZ色彩空间值。
- 计算每个色块的 CIELAB（Lab）值。
- 计算校正后的 Lab 值与参考值之间的色差（如 ΔE94 或 ΔE2000）。
- 通过优化器调整矩阵，最小化色差。
- 迭代计算，直到找到稳定解。
输出最终颜色校正矩阵，用于将RGB转换到目标色彩空间或XYZ色彩空间

三、The Math

1.图像数据结构
彩色图像存储为 m×n×3 数组（高度 × 宽度 × RGB通道）。处理时，图像被展开为 k×3 的二维矩阵 O（k=m×n），每一行对应一个像素的 线性化 RGB 值。

2.颜色校正矩阵
通过一个 3×3 的矩阵 A 对原始数据 O 进行线性变换，得到校正后的矩阵 P：

P = OA

每个校正后的像素通道值（R/G/B）是原始像素三个通道的加权和。例如：

3.线性化要求

输入数据 O 必须是线性亮度值。若原始图像为非线性编码（如 sRGB），需先通过逆 Gamma 变换进行 线性化。校正后的结果 P 可能需要重新应用 Gamma 曲线（去线性化）以适配显示设备。

四、算法迭代逼近

通过调整颜色校正矩阵 A，使校正后的像素矩阵 P = OA 与参考矩阵 R（理想值）之间的差异最小化（常见方法均方误差MSE)。

初始矩阵的构造

初始矩阵 A 的两种形式（3×3 和 4×3）均为对角矩阵，旨在通过均值比例初步对齐原始数据与参考数据的通道增益：

初始值意义：均值比例提供粗略的通道增益，加速优化收敛。

优化算法通过迭代调整颜色校正矩阵 A，使校正后的像素数据 P = OA 逼近参考数据 R。以下是具体步骤及示例：

优化流程

1.定义损失函数
通常采用均方误差（MSE）衡量 P 与 R 的差距：

其中 k 为像素总数，3k 是总通道数（R/G/B）。

2.计算梯度

梯度矩阵 $\frac{\partial Loss}{\partial A}$ 表示损失函数对 A 中各元素的偏导数。通过矩阵运算高效计算：

其中 $O^{T}$ 是原始数据矩阵的转置，P−R 是误差矩阵。

3.更新矩阵 A

使用梯度下降法更新 A：

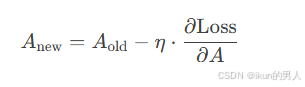
η 为学习率，控制更新步长。

4.迭代优化
重复计算 P、损失、梯度和更新 A，直到损失收敛或达到最大迭代次数

五、计算示例

输入数据 O（2个像素，( k=2））：

$O=\begin{vmatrix} 0.6 & 0.3& 0.8\\ 0.4 &0.5 &0.2 \end{vmatrix}$

参考数据 R：

$R = \begin{vmatrix} 0.7&0.35 &0.9 \\ 0.5&0.6 &0.3 \end{vmatrix}$

初始矩阵 A(3×3)：
根据均值计算初始增益系数：

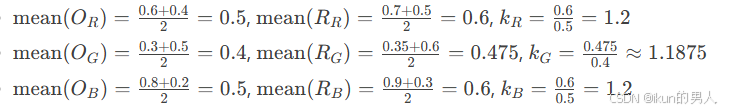
初始矩阵：

$A = \begin{vmatrix} 1.2 & 0 &0 \\ 0&1.1875 &0 \\ 0 & 0 & 1.2 \end{vmatrix}$

学习率：η=0.1

迭代过程

第1次迭代

1.前向计算 $P^{0} = O \cdot A^{0}$

$P^{0} = \begin{vmatrix} 0.72 &0.3563 &0.96 \\ 0.48& 0.5938 & 0.24 \end{vmatrix}$

2.计算损失

$Loss^{0} \approx 0.0037$

3计算梯度

4.更新矩阵 A

$A^{1} = A^{0} - 0.1\cdot \frac{\partial Loss}{\partial A}\approx \begin{vmatrix} 1.2004&0.00055 &0.0012 \\ -0.0004 &1.1879 &-0.0012 \\ 0.0032&0.00056 &1.2036 \end{vmatrix}$