数字图像处理学习笔记第四章频率域滤波

鲸~屿

于 2024-07-01 12:21:54 发布

阅读量1k

点赞数 24

文章标签：学习笔记计算机视觉图像处理

本文链接：https://blog.csdn.net/qq_53034510/article/details/139972138

版权

4.1傅里叶变换

4.1.1傅里叶变换及其反变换

1.为什么要对图像进行变换

图像变换技术——为了有效和快速地对图像进行处理，常常需要将原定义在空域地图像以某种形式转换到另外一些空间，并利用在这些空间的特有性质进行一定的处理，最后再转换回空域以得到所需的效果。

       变换是双向的，或者说需要双向的变换。

              一般将图像从空域向其它空间的变换称为正变换。

              将图像从其它空间向空域的变换称为反变换或逆变换。

2.傅里叶变换及其反变换

一维连续傅里叶变换及反变换

一维连续函数 $f(x)$ 的傅里叶变换 $F(u)$ 定义为： $F(u)=\int_{-\infty }^{\infty }f(x)e^{-j2\pi ux}dx$ ，其中， $j=\sqrt{-1}$ 。

给定 $F(u)$ ，通过傅里叶反变换可以得到 $f(x)$ ： $f(x)=\int_{-\infty }^{\infty }F(u)e^{-j2\pi ux}du$ 。

二维连续傅里叶变换及反变换

二维连续函数 $f(x,y)$ 的傅里叶变换 $F(u,v)$ 定义为： $F(u,v)=\int_{-\infty}^{\infty }\int_{-\infty }^{\infty }f(x,y)e^{-j2\pi (ux+vy)}dxdy$ 。

给定 $F(u,v)$ ，通过傅里叶反变换可以得到 $f(x,y)$ ： $f(x,y)=\int_{-\infty}^{\infty }\int_{-\infty }^{\infty }F(u,v)e^{j2\pi (ux+vy)}dudv$ 。

3.一维离散傅里叶变换 $(DFT)$ 及反变换

一维离散函数 $f(x)(x=0,1,2,......,M-1)$ 的离散傅里叶变换 $F(u)$ 定义为： $F(u)=\frac{1}{M}\sum_{x=0}^{M-1}f(x)e^{\frac{-j2\pi ux}{M}}$

给定 $F(u)(u=0,1,2,...,M-1)$ ，通过离散傅里叶反变换可以得到 $f(x)$ ： $f(x)=\frac{1}{M}\sum_{u=0}^{M-1}F(u)e^{\frac{j2\pi ux}{M}}$

使用欧拉公式可将离散傅里叶变换 $F(u)$ 表述为：

由欧拉公式 $e^{j\theta }=cos\theta +jsin\theta$

可得 $F(u)=\frac{1}{M}\sum_{x=0}^{M-1}f(x)e^{\frac{-j2\pi ux}{M}}$

= $\frac{1}{M}\sum_{x=0}^{M-1}f(x)(cos\frac{2\pi ux}{M}-jsin\frac{2\pi ux}{M})$

傅里叶变换 $F(u)$ 的极坐标表示： $F(u)=|F(u)|e^{-j\varphi (u)}$ ，其中， $\varphi (u)$ 是相位或相位谱。

相位或相位谱为 $\varphi (u)=arctan[\frac{I(u)}{R(u)}]$ ， $R(u)$ 和 $I(u)$ 分别是 $F(u)$ 的实部和虚部；

幅度谱（频谱）为 $|F(u)|=\sqrt{R(u)^{^{2}}+I(u)^{2}}$ ；

功率谱为 $P(u)=|F(u)|^{2}=R(u)^{2}+I(u)^{2}$ 。

4.二维离散傅里叶变换及反变换

（1）大小为 $M\times N$ 的图像 $f(x,y)$ 的 $DFT$ 为：

$F(u,v)=\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi (ux/M+vy/N)}$ ，其中， $u=0,1,2,...,M-1$ ， $v=0,1,2,...,N-1$

对于 $F(u,v)$ ，可通过反 $DFT$ 得到 $f(x,y)$ ，如下：

$f(x,y)=\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}F(u,v)e^{j2\pi (ux/M+vy/N)}$ ，其中， $x=0,1,2,...,M-1$ ， $y=0,1,2,...,N-1$

注：u和v是频率变量，x和y是空域变量。

（2）二维DFT的极坐标表示： $F(u,v)=|F(u,v)|e^{-j\varphi (u,v)}$

相位或相位谱为 $\varphi (u,v)=arctan[\frac{I(u,v)}{R(u,v)}]$ ， $R(u,v)$ 和 $I(u,v)$ 分别是 $F(u,v)$ 的实部和虚部；

幅度谱（频谱）为 $|F(u,v)|=\sqrt{R(u,v)^{^{2}}+I(u,v)^{2}}$ ；

功率谱为 $P(u,v)=|F(u,v)|^{2}=R(u,v)^{2}+I(u,v)^{2}$ 。

（3）关于频谱 $|F(u,v)|$ 的说明

频谱描述了图像中某种频率的成份数量；

频谱中出现的明亮线反映了原始图像的灰度级变化方向（即图像的轮廓线或由灰度急剧变化来表征的内容，其方向与频谱中的明亮线相互垂直）。

4.1.2傅里叶变换的性质

1.可分离性

$F(u,v)=\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi (ux/M+vy/N)}$

$=\frac{1}{M}\sum_{x=0}^{M-1}e^{-j2\pi ux/M}\frac{1}{N}\sum_{y=0}^{N-1}e^{-j2\pi vy/N}$

$=\frac{1}{M}\sum_{x=0}^{M-1}e^{-j2\pi ux/M}F(x,v)$

上式中， $F(x,v)$ 是沿着 $f(x,y)$ 的一行所进行的傅里叶变换结果

当 $x=0,1,2,...,M-1$ ，则沿着 $f(x,y)$ 的所有行计算傅里叶变换

二维傅里叶变换的全过程如下：

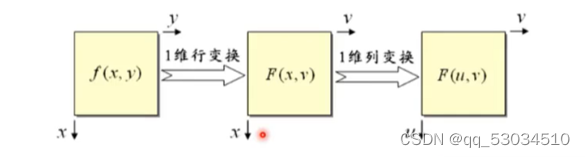
先沿着输入图像的每一行计算一维变换；

再沿中间结果的每一列计算一维变换。

注：可以改变上述顺序，即先列后行；二维傅里叶反变换类似上述过程。

2.平均值

由二维傅里叶变换的定义： $F(u,v)=\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi (ux/M+vy/N)}$

可得 $F(0,0)=\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)$

即图像 $f(x,y)$ 在原点处的傅里叶变换等于图像的平均灰度级。

4.1.3快速傅里叶变换 $(FFT)$

1.为什么需要快速傅里叶变换

对于一维离散函数 $F(u)=\frac{1}{M}\sum_{x=0}^{M-1}f(x)e^{-j2\pi ux/M}$

对u的M个值中的每一个需要进行M次复数乘法（将 $f(x)$ 与 $e^{-j2\pi ux/M}$ 相乘）和M-1次加法，即乘法和加法的次数都正比于 $M^{2}$ ；

快速傅里叶变换 $(FFT)$ 则只需要 $Mlog_{2}M$ 次运算；

$FFT$ 算法与原始变换算法的计算量之比是 $log_{2}M:M$ 。

4.2频率图像增强

4.2.1频率域滤波基础

1.为什么要在频率域研究图像增强

可以利用频率成分和图像外表之间的对应关系

一些在空间域表述的增强任务，在频率域中变得非常普通。

滤波在频率域更为直观，它可以解释空间域滤波的某些性质

利用这些性质进行一定的处理，最后再转换回图像空间，可以得到所需的效果。

空间域和频率域中的滤波器组成了傅里叶变换对

可以在频率域指定滤波器，并对其执行反变换，最后在空间域使用该反变换的结果作为空域滤波器。

2.傅里叶变换的频率分量和图像空间特征之间的联系

变化最慢的的频率成分 $(u=v=0)$ 对应图像的平均灰度级：

$F(0,0)=\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)$

当从变换的原点移开时，低频成分对应图像中灰度慢变化的分量（例如，图像的平滑部分）

进一步偏离原点时，较高的频率成分对应图像中变化越来越快的灰度（例如，边缘或噪声等尖锐部分）

3.频率域滤波的基本思想

使用频率域滤波函数对原始图像的频谱进行滤波，然后对该滤波结果执行反变换来获得处理后的输出图像。

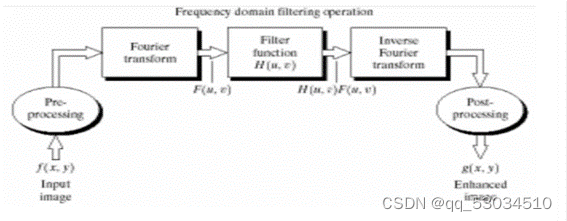
4.频率域滤波的基本步骤

用 $(-1)^{x+y}$ 乘以输入图像 $f(x,y)$ ，使其原点中心化

对步骤1的结果执行 $DFT$ ，得到关于中心对称的频谱 $F(x,v)$

生成一个实的、中心对称的频域滤波器 $H(u,v)$

对滤波器 $H(u,v)$ 、频谱 $F(x,v)$ 执行阵列相乘（对应元素逐个进行相乘），形成乘积 $G(u,v)=H(u,v)F(u,v)$ 且 $0\leqslant m\leqslant M-1$ ， $0\leqslant n\leqslant N-1$

对步骤4的结果 $G(u,v)$ 执行反 $DFT$ ，并取其结果的实部

用 $(-1)^{x+y}$ 乘以步骤5的反 $DFT$ 结果的实部，得到滤波结果 $G(x,y)$

5.频域滤波器如何作用于图像

低通滤波器：使频谱的低频成分通过，同时使其高频成分衰减。被低通滤波的图像比原始图像少了尖锐的细节部分（如噪声、边缘等），但突出了平滑过滤部分；对应于空间域滤波的平滑处理，如均值滤波器。

高通滤波器：使频谱的高频成分通过，同时使其低频成分衰弱。被高通滤波的图像比原始图像少了灰度级的平滑过渡，但突出了边缘等细节部分；对应于空间域的锐化处理，如梯度算子、拉普拉斯算子。

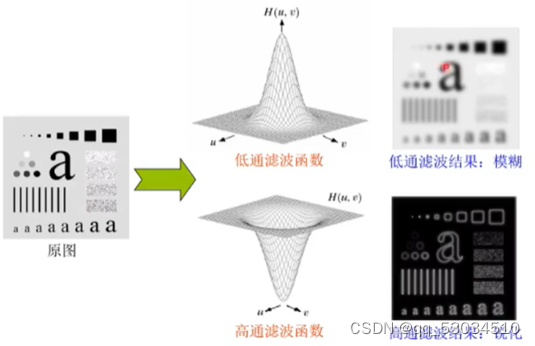
4.2.2频率域低通（平滑）滤波器

1.理想低通滤波器 $(ILPF)$

假设频谱中心在 $(M/2,N/2)$ 处，则任意频谱成分 $(u,v)$ 到中心（原点）的距离 $D(u,v)$ 定义为：

$D(u,v)=\sqrt{(u-\frac{M}{2})^{2}+(v-\frac{N}{2})^{2}}$

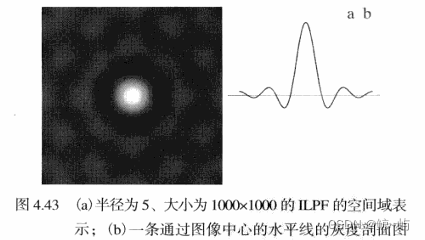
理想低通滤波器H(u,v)滤波器定义为：

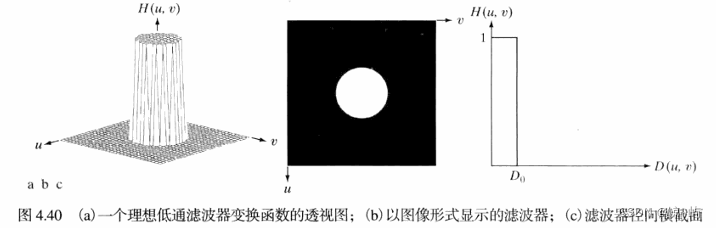
$H(u,v)=\begin{cases} 1 & \text{ if } D(u,v)\leqslant D_{0} \\ 0 & \text{ if } D(u,v) > D_{0} \end{cases}$

说明：在半径为 $D_{0}$ 的圆内，所有频率没有衰减地通过滤波器，而在次半径地圆之外的所有平吕完全被衰减掉。

总图像功率值 $P_{T}=\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}P(u,v)$ ，其中： $P(u,v)=|F(u,v)|^{2}=R(u,v)^{2}+I(u,v)^{2}$

原点位于频谱中心处，半径为 $D_{0}$ 的圆包含 $\alpha$ %的总功率，其中： $\alpha =100[\sum_{u}^{}\sum_{v}^{}P(u,v)/P_{T}]$ 。

注意：总和取处于圆之内或边界线上的 $(u,v)$ 值。

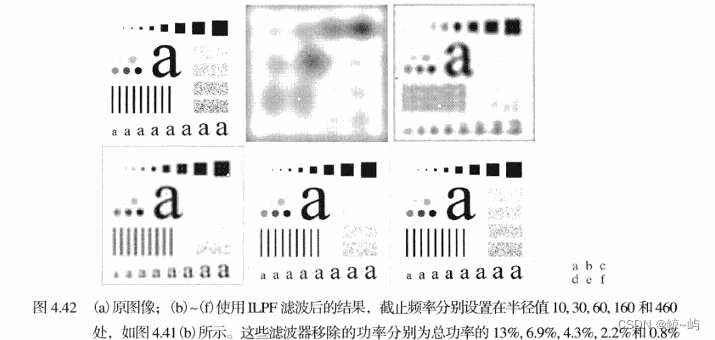
结论：理想低通滤波器产生模糊和振铃现象，且模糊和振铃现象反比于截断频率（也即半径 $D_{0}$ ）。

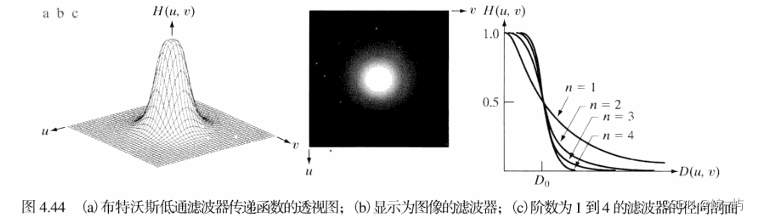
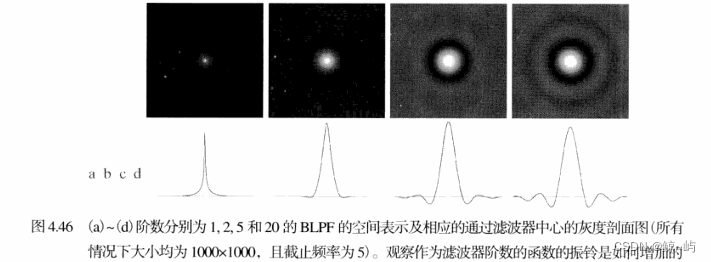
2.巴特沃思低通滤波器

n阶巴特沃思低通滤波器定义如下： $H(u,v)=\frac{1}{1+[D(u,v)/D_{0}]^{2n}}$ ， $D_{0}$ 为截止频率与原点的距离， $D(u,v)$ 是点 $(u,v)$ 与原点的距离。

不同于ILPF，BLPF在通带与被滤除的频率之间没有明显的截断。

当 $D(u,v)=D_{0}$ 时， $H(u,v)=0.5$ ；当 $D(u,v)=0$ 时，滤波器取最大值1。

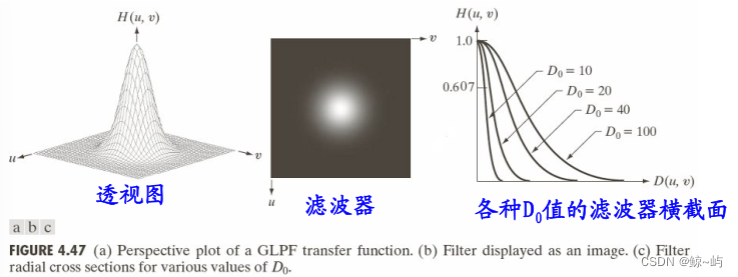
3.高斯低通滤波器

二维高斯低通滤波器定义如下：

$H(u,v)=e^{-D(u,v)^{2}/2\sigma ^{2}}$ ， $\sigma$ 是关于频谱中心的扩展度的度量

令 $\sigma =D_{0}$ ，则二维高斯低通滤波器表示为：

$H(u,v)=e^{-D(u,v)^{2}/2D_{0}^{2}}$ ， $D_{0}$ 为截止频率距原点的距离， $D(u,v)$ 是点 $(u,v)$ 距原点的距离。

随着截止频率的增大，模糊越来越弱；平滑效果稍差于相同截止频率的二阶BLPF；没有出现振铃现象，由于BLPF。

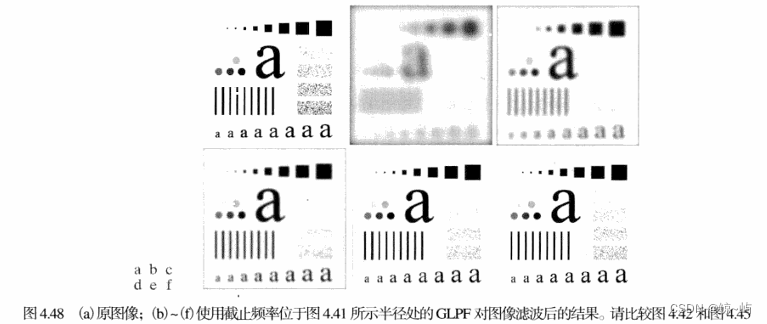
低通滤波器的应用实例：模糊、平滑等

字符识别：通过模糊图像，桥接断裂字符的裂缝

印刷和出版社：从一幅尖锐的原始图像产生平滑、柔和的外观，如人脸，减少皮肤细纹的锐化程度和小斑点。

处理卫星和航空图像：尽可能模糊细节，从而保留大的可识别特征（低通滤波通过消除不重要的特征来简化感兴趣特征的分析）

实例一：用于机器识别系统识别字符的预处理，如打印、传真、复印文本等的字符失真、字符断裂。

实例二：减少人脸图像的皮肤细纹和小斑点

4.2.3频率域高通（锐化）滤波器

1.理想高通滤波器(IHPF)

截止频率距原点的距离为 $D_{0}$ 的IHPF定义为：

$H(u,v)=\begin{cases} 0 & \text{ if } D(u,v)\leqslant D_{0} \\ 1 & \text{ if } D(u,v) > D_{0} \end{cases}$

$D_{0}$ 为截止频率距原点的距离， $D(u,v)$ 是点 $(u,v)$ 距原点的距离。

IHPF的空域表示 $h(u,v)$ ：

实例：

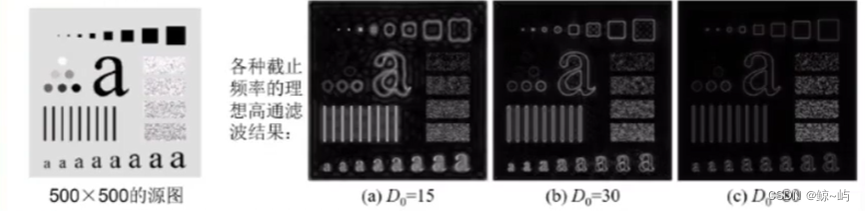
结论：振铃现象明显，a图比b图严重，产生了失真，物体的边界被加粗。

2.巴特沃思高通滤波器

n阶且截止频率距原点的距离为 $D_{0}$ 的BHPF定义为： $H(u,v)=\frac{1}{1+[D_{0}/D(u,v)]^{2n}}$ ， $D_{0}$ 为截止频率与原点的距离， $D(u,v)$ 是点 $(u,v)$ 与原点的距离。

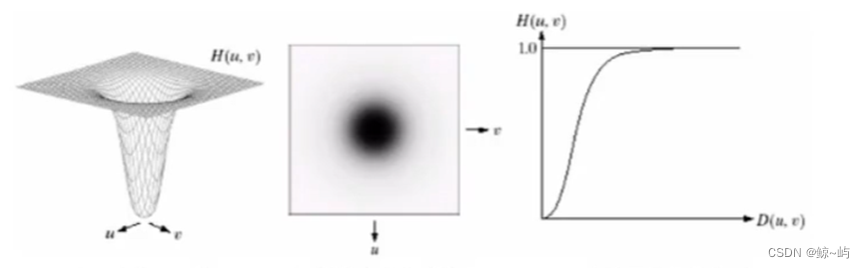
BHPF的空域表示 $h(u,v)$ ：

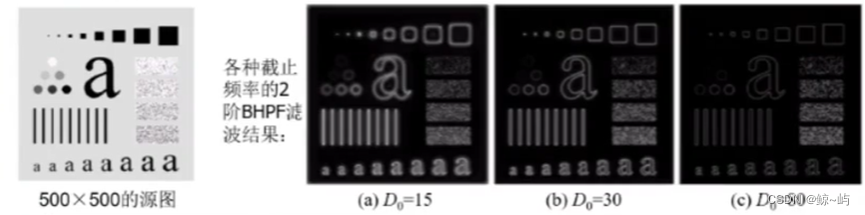
3.高斯高通滤波器

截止频率距原点的距离原点为 $D_{0}$ 的GHPF定义为：

$H(u,v)=1-e^{-D(u,v)^{2}/2D_{0}^{2}}$

$D_{0}$ 为截止频率距原点的距离， $D(u,v)$ 是点 $(u,v)$ 距原点的距离。

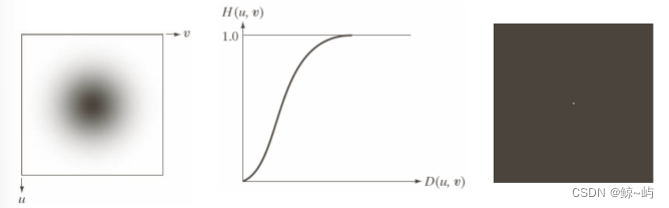
高斯高通滤波实例：

结论：GHPF的结果比BHBF和IHPF的结果更平滑，即使是对微小物体和细线条的滤波也是较清晰的。

4.高频提升滤波和高频加强滤波

高频率波效果等同于用原始图像的频谱减去低通滤波的结果图像频谱。图像经过高通滤波后，其背景的平均强度减小到接近黑色（因为高通滤波器除去了傅里叶变换的零频率成分）。可以把原始图像加到滤波后的结果图像中，即高频提升滤波或高频加强滤波。

（1）高频提升滤波

高频提升滤波可以将原始图像按一定比例加到滤波后的结果中，以保留原始图像的背景。

假设在空域中，原始图像为 $f(x,y)$ ，高通滤波后的结果图像为 $f_{HP}(x,y)$ ，低通滤波后的结果图像为 $f_{LP}(x,y)$ ，高频提升滤波的结果图像为 $f_{HB}(x,y)$ 。则高频提升滤波的空域形式如下：

$f_{HB}(x,y)=A\times f(x,y)-f_{LP}(x,y)$ $(A\geq 1)$

也即： $f_{HB}(x,y)=(A-1)\times f(x,y)+f(x,y)-f_{LP}(x,y)$

$=(A-1)\times f(x,y)+f_{HP}(x,y)$

空域形式： $f_{HB}(x,y)=(A-1)\times f(x,y)+f_{HP}(x,y)$

频域形式： $F_{HB}(u,v)=(A-1)\times F(u,v)+F_{HP}(u,v)$

$F_{HB}(u,v)=(A-1)\times F(u,v)+H_{HP}(u,v)\times F(u,v)$

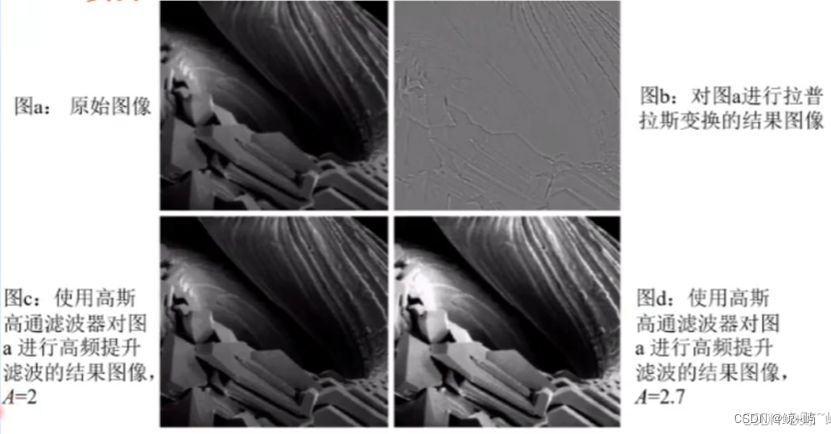
（2）高频加强滤波

高频加强滤波可以加强增强图像的高频成分。在高通滤波器函数以前乘以一个常数，在增加一个偏移量以便使零频率不被滤波器滤除掉。

高通滤波： $G(u,v)=H_{HP}(u,v)\times F(u,v)$

高频加强滤波器： $H_{E}(u,v)=k\times H_{HP}(u,v)+c$

高频加强滤波： $G_{E}(u,v)=H_{E}(u,v)\times F(u,v)$

$=[k\times H_{HP}(u,v)+c]\times F(u,v)$

$=k\times H_{HP}(u,v)\times F(u,v)+c\times F(u,v)$

$=k\times G(u,v)+c\times F(u,v)$

参考文献：数字图像处理（第四版）冈萨雷斯

鲸~屿

关注

24
点赞
踩
13

收藏

觉得还不错? 一键收藏
0
评论
数字图像处理学习笔记第四章频率域滤波

对应于空间域滤波的平滑处理，如均值滤波器。图像变换技术——为了有效和快速地对图像进行处理，常常需要将原定义在空域地图像以某种形式转换到另外一些空间，并利用在这些空间的特有性质进行一定的处理，最后再转换回空域以得到所需的效果。结论：GHPF的结果比BHBF和IHPF的结果更平滑，即使是对微小物体和细线条的滤波也是较清晰的。印刷和出版社：从一幅尖锐的原始图像产生平滑、柔和的外观，如人脸，减少皮肤细纹的锐化程度和小斑点。当从变换的原点移开时，低频成分对应图像中灰度慢变化的分量（例如，图像的平滑部分）
复制链接

扫一扫