【序列匹配算法】Needleman Wunsch算法 v2.0

Domainmain

已于 2024-12-06 11:41:14 修改

阅读量4.3k

点赞数 17

分类专栏： Python算法学习与设计文章标签：算法

于 2022-11-15 15:39:19 首次发布

本文链接：https://blog.csdn.net/qq_54501547/article/details/127863580

版权

Python算法学习与设计专栏收录该内容

2 篇文章

订阅专栏

之前发布了Needleman Wunsch算法v1.0的作品，存在着没有算法讲解（我有点lazy）、只能返回一条路径、返回路径有误等等问题。经过不断的改进，现发布Needleman Wunsch算法v2.0！

更新内容：

将匹配有误的地方进行了纠正。
可以返回所有匹配结果而不只是一条！
基于非递归的图搜索思想，思路新颖。
增加了矩阵可视化的内容。

接下来，我们就从什么是Needleman Wunsch算法开始。（想直接看完整代码请跳到最后）

Needleman Wunsch算法是用于两条序列全局匹配的经典算法，本质上是动态规划的思想，即：第(i,j)处的最佳匹配=第(i,j)之前所有的最佳匹配+i和j的最佳匹配。

如何确定“最佳”呢？就由计分规则来决定。在这个版本下，笔者采用最简单的打分方式：

两个位点匹配（如A与A配对）：以+9分为例
两个位点不匹配（如A与C不配对）：以-6分为例
有插入突变或删除突变（如A与-或-与A）：以-2分为例

在给定计分规则下，数学上可证明能给出具有最高（优）比对打分的比对结果。

如何实现呢？我们以碱基配对为例。假设我们要匹配：

序列1 AACGTACTCAAGTCT
序列2 TCGTACTCTAACGAT

首先，做点准备工作。我们定义file函数和str_to_list函数。file函数帮助我们通过读取文件的方式获得序列，不过要求一个文件中只有一条序列；str_to_list函数帮助我们将序列字符串转化为字符列表的形式，如将“AATC”转化为["A", "A", "T", "C"]，方便后续访问每个位点的名称。

# %% 导入序列
def file(path: str):
    """
    导入文件中的序列
    path: 文件路径
    """
    with open(path) as file_obj:
        seq = file_obj.read()
    # 返回序列
    return seq

# %% 初始化
def str_to_list(a: str, b: str):
    """
    将序列字符串转换为单个字符列表
    a: 序列一
    b: 序列二
    """
    return list(a), list(b)

接下来，我们需要初始化打分矩阵。如果两条序列的长度为a和b，那么打分矩阵的维度为(a+1)×(b+1)，且矩阵中每个元素都为0；之后更新上边缘和左边缘的数值，由于横竖移动的得分都是gap得分，所以初始化的矩阵应该长这样：

初始化这个矩阵的代码为：

def ini_matrix(l1: list, l2: list, gap):
    """
    初始化罚分矩阵并计算边缘分值
    l1: 序列一列表
    l2: 序列二列表
    gap: 空位得分
    """
    # 获取序列长度构建初始矩阵
    n1 = len(l1)
    n2 = len(l2)
    score_matrix = np.zeros((n1+1, n2+1))
    # 初始化边缘分
    for i in range(1, n1+1):
        score_matrix[i][0] += gap * i
    for j in range(1, n2+1):
        score_matrix[0][j] += gap * j
    # 返回矩阵
    return score_matrix

接着我们要开始逐步填充这个矩阵了。怎么填充呢？

我们先看这个格子：

这个格子的计算依赖三个邻居格子：左、上、左上。

从左边来的格子算出黄色格子的得分为-2-2=-4；
从上边来的格子算出黄色格子的得分为-2-2=-4；
从对角线格子计算，由于黄色格子对应的A与T不匹配，所以分数为0-6=-6

这三个分数中取最大值-4作为黄色格子的值，即：

同理，我们把剩下所有的格子都计算完毕，结果如图所示：

代码如下：

# %% 计分
def score(matrix: np.array, l1: list, l2: list, match, mismatch, gap):
    """
    计算矩阵得分
    matrix: 初始化的矩阵
    l1: 序列一列表
    l2: 序列二列表
    match: 匹配得分
    mismatch: 不匹配时得分
    gap: 空位得分
    """
    # 循环计分
    for i in range(1, len(l1)+1):
        for j in range(1, len(l2)+1):
            # 计算三类分值
            from_left = matrix[i][j - 1] + gap  # 从左到右空位
            from_above = matrix[i - 1][j] + gap  # 从上到下空位
            if l1[i-1] == l2[j-1]:  # 对角线
                from_diag = matrix[i - 1][j - 1] + match  # 匹配
            else:
                from_diag = matrix[i - 1][j - 1] + mismatch  # 不匹配
            # 比较并赋分
            matrix[i][j] = max(from_left, from_above, from_diag)
    return matrix

得到打分矩阵后，下一步就是回溯。如何回溯呢？

首先，Needleman Wunsch算法的回溯起点为右下角的方格；

其次，回溯基本思想就是看第(i,j)个格子是从哪些邻居格子中计算而来。举个例子：

如图，右下角的方格83，它可以是由方格74通过+9得来（因为方格83的横纵碱基T与T匹配，所以74+9=83），也可以通过上方格85-2得到（gap），这样就会导致回溯路径有多条，那怎么操作呢？

一般来说，可以用递归的办法解决，因为代码量很低，但是递归对时间和空间的耗费比较大；非递归的办法虽然看起来麻烦，但是可以锻炼自己的代码能力，所以笔者尝试使用非递归的方式来实现。

非递归的实现困扰了笔者很久，但是我突然有一天在网上冲浪的时候找到了灵感：基于图路径搜索的思想进行回溯！如何做呢？

1.首先，我们定义两个栈，一个为主栈，另一个为辅助栈，大概长这样：

2.然后将右下角的元素（暂且理解为v1）入主栈：

3.接下来更新v1的“邻居”，也就是v1是从哪些格子里计算得来的。条件如下：

如果v1是匹配的，且等于对角线+9，那么考虑对角线；
如果v1不匹配，且等于对角线-6，那么也考虑对角线；
如果v1来自左边格子/上边格子-2，那么就考虑左边格子/上边格子

如此一来，我们假设v1有邻居v2,v3，将它们放入辅助栈：

4.下一步，因为辅助栈栈顶元素非空，所以弹出一个邻居到主栈中去：

重复上述3与4，更新v3的邻居。

5.什么时候结束呢？到左上角元素就结束，假设长这样：

假设v6就是左上角那个(0,0)元素，那么说明主栈找到了通路，就打印主栈所有元素，同时弹出主栈栈顶元素。

弹出后继续检查：

如果辅助栈的栈顶是非空列表，那么还要重复3与4，寻找新的序列；
如果辅助栈栈顶是空列表，那么主辅栈同时弹出元素。

整个程序结束条件：主栈栈空！

基于上述的想法，编写这样的回溯函数，获得所有匹配结果的路径索引：

# %% 回溯
def trace_back(res: np.array, l1: list, l2: list, match, mismatch, gap):
    """
    回溯矩阵获得匹配结果索引
    res: 结果矩阵
    l1: 序列一列表
    l2: 序列二列表
    match: 匹配得分
    mismatch: 不匹配时得分
    gap: 空位得分
    """
    path = []    # 最终所有路径
    m_stack = [(len(l1), len(l2))]  # 主栈
    a_stack = []  # 辅助栈
    while m_stack:  # 当主栈非空时
        # 检查是否到终点
        if m_stack[-1] != (0, 0):
            # 检查主辅栈长度是否一致，不一致则添加新邻居
            if len(m_stack) > len(a_stack):
                a_stack.append([])
                row = m_stack[-1][0]
                col = m_stack[-1][1]
                if l1[row - 1] == l2[col - 1] and res[row][col] == res[row-1][col-1]+match:
                    a_stack[-1].append((row-1, col-1))
                elif res[row][col] == res[row-1][col-1]+mismatch:
                    a_stack[-1].append((row-1, col-1))
                if res[row][col] == res[row-1][col]+gap:
                    a_stack[-1].append((row-1, col))
                if res[row][col] == res[row][col-1]+gap:
                    a_stack[-1].append((row, col-1))
            # 检测辅栈栈顶列表是否为空，不空则可以访问邻居
            elif a_stack[-1] != []:
                m_stack.append(a_stack[-1].pop())
            # 辅助栈为空，则同时退栈一个
            elif a_stack[-1] == []:
                a_stack.pop()
                m_stack.pop()
        else:
            # 到终点，存储索引路径，依次弹出栈顶
            path.append(m_stack.copy())
            m_stack.pop()
    return path

获得路径索引之后，就需要将路径索引对应的碱基打印出来，我们之前用到的str_to_list的结果就比较方便了，只要访问路径索引，找到对应碱基即可。代码中我还加入了特殊连接符的部分，具体效果就是输出时匹配的碱基中间就加一个“|”，不匹配加“*”，具体效果看后续输出。

# %% 将回溯结果转化为碱基
def trace_to_base(match: list, l1: list, l2: list): 
    """
    将回溯获得的索引转化为对应的碱基并打印
    match: 回溯索引元组列表
    l1: 序列一列表
    l2: 序列二列表
    """
    seq_match1 = []
    seq_match2 = []
    connect = []  # 连接符
    # 依次转换
    for index in range(1, len(match)):
        if match[index][0] != match[index - 1][0] and match[index][1] != match[index-1][1]:
            seq_match1.append(l1[match[index][0] - 1])
            seq_match2.append(l2[match[index][1] - 1])
            if l1[match[index][0] - 1] == l2[match[index][1] - 1]:
                connect.append("|")
            else:
                connect.append("*")
        elif match[index][0] == match[index - 1][0]:
            seq_match1.append("-")
            seq_match2.append(l2[match[index][1] - 1])
            connect.append(" ")
        elif match[index][1] == match[index - 1][1]:
            seq_match1.append(l1[match[index][0] - 1])
            seq_match2.append("-")
            connect.append(" ")
    # 转换为字符串
    seq_match1 = "".join(seq_match1)
    seq_match2 = "".join(seq_match2)
    connect = "".join(connect)
    return seq_match1, seq_match2, connect

最后一个辅助函数就是可视化的函数，笔者通过imshow函数绘制出了得分矩阵热图，并通过设置参数plot_val来判断是否要把得分矩阵的实际数值也画在上面，路径覆盖的方格用不同颜色的数字标记出来。具体的算法过程就不细说了：

# %% 可视化
def matrix_visual(res_matrix: np.array, l1: list, l2: list, index: list, plot_val=False):
    """
    可视化得分矩阵
    res_matrix: 得分矩阵
    l1: 序列一列表
    l2: 序列二列表
    index: 回溯的索引列表
    plot_val: 逻辑值,是否将矩阵数值绘制在图中,默认为False
    """
    # 处理index列表
    path = set()
    for i in index:
        path = set(i).union(path)
    # 可视化得分矩阵
    fig, ax = plt.subplots()
    visual_matrix = plt.imshow(res_matrix)
    plt.colorbar(visual_matrix)
    # 修改轴
    l1.insert(0, '0')
    l2.insert(0, '0')
    ax.set_xticks(np.arange(0, len(l1)), minor=False)
    ax.set_yticks(np.arange(0, len(l2)), minor=False)
    ax.xaxis.set_ticks_position('top')
    ax.xaxis.set_label_position('top')
    ax.set_xticklabels(l1)
    ax.set_yticklabels(l2)
    plt.xlabel("Sequence 1")
    plt.ylabel("Sequence 2")
    # 是否画出标记
    if plot_val:
        for i in range(len(l2)):
            for j in range(len(l1)):
                if (j, i) in path:
                    ax.text(i-0.35, j+0.1,
                            res_matrix[j][i], fontsize=6, color="#FF49F5")
                else:
                    ax.text(i-0.35, j+0.1, res_matrix[j][i], fontsize=6)
    # 紧密排布
    plt.tight_layout()
    plt.show()

最后就是我们的主函数啦！按照执行顺序把他们封装在一起，方便后续调用：

# %% 主函数
def nw(seq1: str, seq2: str, match, mismatch, gap, plot=False, plot_val=False):
    """
    主函数
    seq1: 第一条序列
    seq2: 第二条序列
    match: 匹配得分
    mismatch: 不匹配时得分
    gap: 空位得分
    plot: 逻辑值,是否画出得分矩阵,默认不画出
    plot_val: 逻辑值,是否将矩阵数值绘制在图中,默认为False 
    """
    # 开始计时
    print("\n开始匹配......")
    start = time.time()
    # 获取列表
    l1, l2 = str_to_list(seq1, seq2)
    # 初始化打分矩阵
    score_matrix = ini_matrix(l1, l2, gap)
    # 为矩阵赋分
    res_matrix= score(score_matrix, l1, l2, match, mismatch, gap)
    # 回溯
    path = trace_back(res_matrix, l1, l2, match, mismatch, gap)
    # 停止计时
    stop = time.time()
    print("匹配结束!\n********************")
    # 打印最终结果
    print("打印比对结果......")
    for i in path:
        i = i[::-1]
        seq_match1, seq_match2, connect = trace_to_base(i, l1, l2)
        print(seq_match1)
        print(connect)
        print(seq_match2)
        print("--------------------")
    print("匹配结果共计%s条, 匹配分数为: %s"%(len(path), res_matrix[-1][-1]))
    print("\n计算耗时为: ", stop - start, "秒")
    if plot:
        print("\n可视化得分矩阵......")
        matrix_visual(res_matrix, l1, l2, path, plot_val)
    print("\n结束!!!")

最后我们看一看效果：

# %% 应用
seq1 = "AACGTACTCAAGTCT"
seq2 = "TCGTACTCTAACGAT"
nw(seq1, seq2, match=9, mismatch=-6, gap=-2, plot=True, plot_val=True)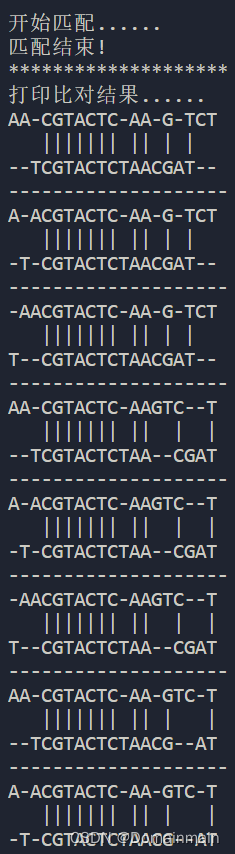

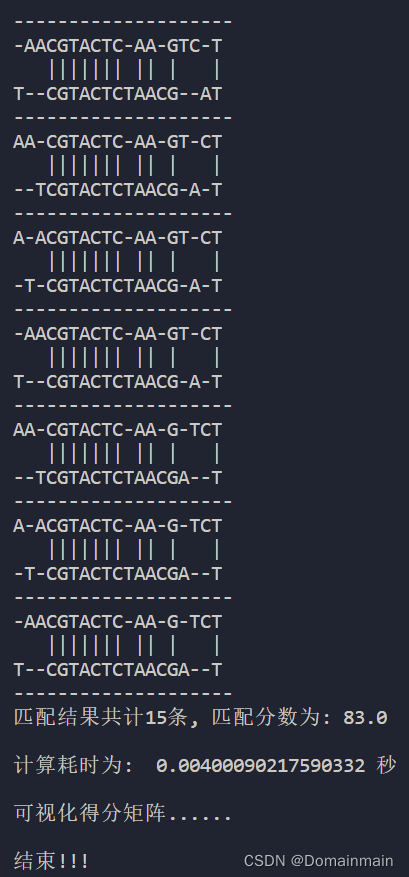
结果是正确的，返回了15条路径！

最后附上所有的代码：

# %% 导入包
import numpy as np
import matplotlib.pyplot as plt
import time

# %% 导入序列
def file(path: str):
    """
    导入文件中的序列
    path: 文件路径
    """
    with open(path) as file_obj:
        seq = file_obj.read()
    # 返回序列
    return seq

# %% 初始化
def str_to_list(a: str, b: str):
    """
    将序列字符串转换为单个字符列表
    a: 序列一
    b: 序列二
    """
    return list(a), list(b)

def ini_matrix(l1: list, l2: list, gap):
    """
    初始化罚分矩阵并计算边缘分值
    l1: 序列一列表
    l2: 序列二列表
    gap: 空位得分
    """
    # 获取序列长度构建初始矩阵
    n1 = len(l1)
    n2 = len(l2)
    score_matrix = np.zeros((n1+1, n2+1))
    # 初始化边缘分
    for i in range(1, n1+1):
        score_matrix[i][0] += gap * i
    for j in range(1, n2+1):
        score_matrix[0][j] += gap * j
    # 返回矩阵
    return score_matrix

# %% 计分
def score(matrix: np.array, l1: list, l2: list, match, mismatch, gap):
    """
    计算矩阵得分
    matrix: 初始化的矩阵
    l1: 序列一列表
    l2: 序列二列表
    match: 匹配得分
    mismatch: 不匹配时得分
    gap: 空位得分
    """
    # 循环计分
    for i in range(1, len(l1)+1):
        for j in range(1, len(l2)+1):
            # 计算三类分值
            from_left = matrix[i][j - 1] + gap  # 从左到右空位
            from_above = matrix[i - 1][j] + gap  # 从上到下空位
            if l1[i-1] == l2[j-1]:  # 对角线
                from_diag = matrix[i - 1][j - 1] + match  # 匹配
            else:
                from_diag = matrix[i - 1][j - 1] + mismatch  # 不匹配
            # 比较并赋分
            matrix[i][j] = max(from_left, from_above, from_diag)
    return matrix

# %% 回溯
def trace_back(res: np.array, l1: list, l2: list, match, mismatch, gap):
    """
    回溯矩阵获得匹配结果索引
    res: 结果矩阵
    l1: 序列一列表
    l2: 序列二列表
    match: 匹配得分
    mismatch: 不匹配时得分
    gap: 空位得分
    """
    path = []    # 最终所有路径
    m_stack = [(len(l1), len(l2))]  # 主栈
    a_stack = []  # 辅助栈
    while m_stack:  # 当主栈非空时
        # 检查是否到终点
        if m_stack[-1] != (0, 0):
            # 检查主辅栈长度是否一致，不一致则添加新邻居
            if len(m_stack) > len(a_stack):
                a_stack.append([])
                row = m_stack[-1][0]
                col = m_stack[-1][1]
                if l1[row - 1] == l2[col - 1] and res[row][col] == res[row-1][col-1]+match:
                    a_stack[-1].append((row-1, col-1))
                elif res[row][col] == res[row-1][col-1]+mismatch:
                    a_stack[-1].append((row-1, col-1))
                if res[row][col] == res[row-1][col]+gap:
                    a_stack[-1].append((row-1, col))
                if res[row][col] == res[row][col-1]+gap:
                    a_stack[-1].append((row, col-1))
            # 检测辅栈栈顶列表是否为空，不空则可以访问邻居
            elif a_stack[-1] != []:
                m_stack.append(a_stack[-1].pop())
            # 辅助栈为空，则同时退栈一个
            elif a_stack[-1] == []:
                a_stack.pop()
                m_stack.pop()
        else:
            # 到终点，存储索引路径，依次弹出栈顶
            path.append(m_stack.copy())
            m_stack.pop()
    return path

# %% 将回溯结果转化为碱基
def trace_to_base(match: list, l1: list, l2: list): 
    """
    将回溯获得的索引转化为对应的碱基并打印
    match: 回溯索引元组列表
    l1: 序列一列表
    l2: 序列二列表
    """
    seq_match1 = []
    seq_match2 = []
    connect = []  # 连接符
    # 依次转换
    for index in range(1, len(match)):
        if match[index][0] != match[index - 1][0] and match[index][1] != match[index-1][1]:
            seq_match1.append(l1[match[index][0] - 1])
            seq_match2.append(l2[match[index][1] - 1])
            if l1[match[index][0] - 1] == l2[match[index][1] - 1]:
                connect.append("|")
            else:
                connect.append("*")
        elif match[index][0] == match[index - 1][0]:
            seq_match1.append("-")
            seq_match2.append(l2[match[index][1] - 1])
            connect.append(" ")
        elif match[index][1] == match[index - 1][1]:
            seq_match1.append(l1[match[index][0] - 1])
            seq_match2.append("-")
            connect.append(" ")
    # 转换为字符串
    seq_match1 = "".join(seq_match1)
    seq_match2 = "".join(seq_match2)
    connect = "".join(connect)
    return seq_match1, seq_match2, connect

# %% 可视化
def matrix_visual(res_matrix: np.array, l1: list, l2: list, index: list, plot_val=False):
    """
    可视化得分矩阵
    res_matrix: 得分矩阵
    l1: 序列一列表
    l2: 序列二列表
    index: 回溯的索引列表
    plot_val: 逻辑值,是否将矩阵数值绘制在图中,默认为False
    """
    # 处理index列表
    path = set()
    for i in index:
        path = set(i).union(path)
    # 可视化得分矩阵
    fig, ax = plt.subplots()
    visual_matrix = plt.imshow(res_matrix)
    plt.colorbar(visual_matrix)
    # 修改轴
    l1.insert(0, '0')
    l2.insert(0, '0')
    ax.set_xticks(np.arange(0, len(l1)), minor=False)
    ax.set_yticks(np.arange(0, len(l2)), minor=False)
    ax.xaxis.set_ticks_position('top')
    ax.xaxis.set_label_position('top')
    ax.set_xticklabels(l1)
    ax.set_yticklabels(l2)
    plt.xlabel("Sequence 1")
    plt.ylabel("Sequence 2")
    # 是否画出标记
    if plot_val:
        for i in range(len(l2)):
            for j in range(len(l1)):
                if (j, i) in path:
                    ax.text(i-0.35, j+0.1,
                            res_matrix[j][i], fontsize=6, color="#FF49F5")
                else:
                    ax.text(i-0.35, j+0.1, res_matrix[j][i], fontsize=6)
    # 紧密排布
    plt.tight_layout()
    plt.show()

# %% 主函数
def nw(seq1: str, seq2: str, match, mismatch, gap, plot=False, plot_val=False):
    """
    主函数
    seq1: 第一条序列
    seq2: 第二条序列
    match: 匹配得分
    mismatch: 不匹配时得分
    gap: 空位得分
    plot: 逻辑值,是否画出得分矩阵,默认不画出
    plot_val: 逻辑值,是否将矩阵数值绘制在图中,默认为False 
    """
    # 开始计时
    print("\n开始匹配......")
    start = time.time()
    # 获取列表
    l1, l2 = str_to_list(seq1, seq2)
    # 初始化打分矩阵
    score_matrix = ini_matrix(l1, l2, gap)
    # 为矩阵赋分
    res_matrix= score(score_matrix, l1, l2, match, mismatch, gap)
    # 回溯
    path = trace_back(res_matrix, l1, l2, match, mismatch, gap)
    # 停止计时
    stop = time.time()
    print("匹配结束!\n********************")
    # 打印最终结果
    print("打印比对结果......")
    for i in path:
        i = i[::-1]
        seq_match1, seq_match2, connect = trace_to_base(i, l1, l2)
        print(seq_match1)
        print(connect)
        print(seq_match2)
        print("--------------------")
    print("匹配结果共计%s条, 匹配分数为: %s"%(len(path), res_matrix[-1][-1]))
    print("\n计算耗时为: ", stop - start, "秒")
    if plot:
        print("\n可视化得分矩阵......")
        matrix_visual(res_matrix, l1, l2, path, plot_val)
    print("\n结束!!!")

# %% 应用
seq1 = "AACGTACTCAAGTCT"
seq2 = "TCGTACTCTAACGAT"
nw(seq1, seq2, match=9, mismatch=-6, gap=-2, plot=True, plot_val=True)