目录
无监督学习1--聚类
什么是无监督学习？
训练集只有x1，x2...,xi，没有标签y的数据。
我们要将无标签的数据输入，然后让算法找到一些隐含在数据中的结构，
把这些无标签的数据分成一簇一簇的，就是聚类算法(学习的第一个无监督学习的算法)。
聚类有哪些应用？
K-means算法
语言表述步骤
给定一组未加标签的数据集，希望有一个算法能够自动的讲这些数据分成有紧密关系的子集或簇。
K-means算法 是目前比较热门，应用较多的算法之一。
K-mean步骤：假如下图我想把数据分成两个簇
首先随机生成两点，这两点叫做聚类中心，K-means是一个迭代算法，做两件事：第一件 簇分配，第二个 移动聚类中心。簇分类时：需要遍历每个数据，根据它与两个随机点的距离那个近，就把这个数据分配给那个点。移动聚类中心：找到所有同颜色的点计算其均值的位置为新的聚类中心。然后再次计算每个点距离中心点的距离分，重复这两个步骤，直到中心点不再改变。
伪代码表示k-means的过程
说明：假设uk是某个簇的均值，如果存在一个没有点的聚类中心，直接移除这个聚类中心，最终会得到K-1个簇；如果想要最终的到K个簇，那么需要重新初始化聚类中心；但最常见的做法，一般是直接移除。
常应用来解决分离不佳的簇的问题
例如将根据体重设计衣服的尺寸(S,L,M)
优化目标
K：表示簇的数量；k：表示聚类中心点的下标，c^i:表示xi被划分到第几个簇。
K-means的代价函数为下图中的J，算法最终要找到c^i,μ_i，即能最小化J的参数值。这个代价函数有时也叫做 失真代价函数 或 K-means的失真。 J->畸变函数
随机初始化
如何使算法避免局部最优解？
初始化点不同，结果也不同。
初始化选择的点可能会使结果陷入局部最优，如下图右下角两张图所示。
要避免陷入局部最优，我们需要做多次初始化而不是一次。来保证最终得到的是最优的。
常见的初始化次数在 50到1000次。当然如果K比较小，次数少一些。
选取聚类数量
目前还没有可以自动选择聚类的数目的算法，需要通过可视化数据或观察聚类的输出来选择(手动)
"肘部法则"
如果得到左图的曲线，是好的，但通常得到的图是右图，无法判断那个点，所以相当于啥都没做。
因此不要期望它每次都有用。
下面仍然以衣服尺寸聚类为例：
衣服的销售量可能会帮你决定分成几类，怎样利用后续的目的决定什么样的衣服作为评价标准来选择聚类数。手动选择时，想想聚类的目的是什么？
无监督学习2--降维
目标1---数据压缩
压缩可以减小占用的空间，可以使学习算法运行的更快。
图一-->图二(将数据投影到一个平面)-->最后降到二维空间表示
目标2---可视化
PCA(也叫 主成分分析)
主成分分析问题规划1
PCA问题的公式描述
公式描述即用公式描述PCA的用途。 Principal component analysis（主成分分析）
数学证明过于复杂，因此这里没有数学证明u和z为什么可以这么用。
如下图：对于一个二维数据我们想找到一条直线，将点投影到这条直线上，它会找到一个低维平面(这里是一条直线)，将点投影到这个面上，每个点与投影之间的距离叫做"投影误差"，PCA会选择误差平方最小的面或线作为投影面或线，以便最小化平法投影误差。 
PCA与线性回归
首先，PCA不是线性回归，他们是两种不同的算法，他们计算的误差是不一样的，如下图所示。
主成分分析问题规划2
数据处理
无监督学习中，均值标准化过程(使每个特征具有均值为0的特点)与特征缩放(根据数据集决定)过程很相似。
计算u^(i),z的描述过程如下图，协方差用∑(大写的σ:一个协方差矩阵)表示，式子左边为协方差，右面是求和符号。svd:表示奇异值分解。不同语言找有这个功能的库就行了。
总结
进行均值归一化后为确保每一个特征都是均值为0的。根据数据范围任选特征缩放。预处理完后计算载体矩阵Sigma，通过这个方法，如果你的数据 是被给予作为一个矩阵如图中的X训练集矩阵，然后我们先得到要降维矩阵U的前k列，z=..定义了我们如何从一个特征向量x到降维的表示z。
主成分数量选择
我们希望在平均 均方误差与训练集方差的比例尽可能小的情况下选择尽可能小的 k值（从n个特征降到k个特征）如果我们希望这个比例小于1%，就意味着原本数据的偏差有99%都保留下来了，如果我们选择保留90%的偏差，便能非常显著地降低模型中特征的维度了。
我们可以先令k=1，然后进行主成分分析，获得U_{reduce}Ureduce和z，然后计算比例是否小于1%。如果不是的话再令k=2，依次类推，直到找到可以使得比例小于1%的最小k值（因为各个特征之间通常情况存在某种相关性).其中的 S是一个n×n 的矩阵，只有对角线上有值，而其它单元都是 0，我们可以使用这个矩阵来计算平均均方误差与训练集方差的比例：
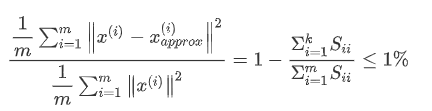
即：
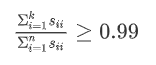
压缩重现
重现即怎么从压缩后的数据得到之前的数据表示？
应用PCA的建议
首先，我们尝尝使用PCA加速无监督学习算法。假设你有一个监督学习的数据，其中x^i有很高的维度，实际中这可能是一个计算机视觉的问题。即假设我们有一张 100×100 像素的图片包含10000 个像素强度值，对于这种很高维的特征向量，运行学习算法时很慢。这是用PCA降低它的维度，步骤如下：
-
首先，抽出x，不看y；运用PCA将数据压缩至1000个特征
-
然后，对训练集运行某个学习算法:逻辑回归、SVM、神经网络等
-
最后，如果有一个新的样本，将新的测试样本x经过PAC的映射关系进行映射获得相应的z，然后把z带到假设函数中
-
note:PCA定义一个从x到z的映射，这个映射只能通过在训练集上运行PCA来定义。所做的是计算一系列参数进行特征缩放和均值归一化，它还计算矩阵U_reduce(只能从训练集上训练得出)
错误的使用PCA的情况： -
认为PCA是一种防止过拟合的方法。防止过拟合的最好的办法 正则化。原因在于PCA只是近似地丢弃掉一些特征，它并不考虑任何与y有关的影响，因此可能会丢失非常重要的特征。
-
默认地将PCA作为学习过程中的一部分，这虽然很多时候有效果，建议在使用PCA前先从所有原始特征开始，只在当你确定用x无法运行时（算法运行太慢或者占用太多内存）再考虑采用PCA。
-
总:PCA应用于提高算法运行效率、数据压缩、可视化。
K-means应用ex7
1.一个简单的二维数据集
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat
def find_closest_centroids(X, centroids):
m = X.shape[0]
k = centroids.shape[0]
idx = np.zeros(m)
for i in range(m):
min_dist = 1000000
for j in range(k):
dist = np.sum((X[i,:] - centroids[j,:]) ** 2)
if dist < min_dist:
min_dist = dist
idx[i] = j
return idx
data = loadmat('E:/Python/machine learning/data/ex7data2.mat')
X = data['X']
initial_centroids = initial_centroids = np.array([[3, 3], [6, 2], [8, 5]])
idx = find_closest_centroids(X, initial_centroids)
idx[0:3]array([0., 2., 1.])
data2 = pd.DataFrame(data.get('X'), columns=['X1', 'X2'])
data2.head()| X1 | X2 | |
|---|---|---|
| 0 | 1.842080 | 4.607572 |
| 1 | 5.658583 | 4.799964 |
| 2 | 6.352579 | 3.290854 |
| 3 | 2.904017 | 4.612204 |
| 4 | 3.231979 | 4.939894 |
#数据可视化
sb.set(context="notebook", style="white")
sb.lmplot('X1', 'X2', data=data2, fit_reg=False)
plt.show()
def compute_centroids(X, idx, k):
m, n = X.shape
centroids = np.zeros((k, n))
for i in range(k):
indices = np.where(idx == i)
centroids[i,:] = (np.sum(X[indices,:], axis=1) / len(indices[0])).ravel()
return centroids
compute_centroids(X, idx, 3)array([[1.95399466, 5.02557006],
[3.04367119, 1.01541041],
[6.03366736, 3.00052511]])
# 将样本分配给最近的簇并重新计算簇的聚类中心
def run_k_means(X, initial_centroids, max_iters):
m, n = X.shape
k = initial_centroids.shape[0]
idx = np.zeros(m)
centroids = initial_centroids
for i in range(max_iters):
idx = find_closest_centroids(X, centroids)
centroids = compute_centroids(X, idx, k)
return idx, centroids
idx, centroids = run_k_means(X, initial_centroids, 10)
cluster1 = X[np.where(idx == 0)[0],:]
cluster2 = X[np.where(idx == 1)[0],:]
cluster3 = X[np.where(idx == 2)[0],:]
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(cluster1[:,0], cluster1[:,1], s=30, color='r', label='Cluster 1')
ax.scatter(cluster2[:,0], cluster2[:,1], s=30, color='g', label='Cluster 2')
ax.scatter(cluster3[:,0], cluster3[:,1], s=30, color='b', label='Cluster 3')
ax.legend()
plt.show()
# 创建一个选择随机样本并将其用作初始聚类中心的函数
def init_centroids(X, k):
m, n = X.shape
centroids = np.zeros((k, n))
idx = np.random.randint(0, m, k)
for i in range(k):
centroids[i,:] = X[idx[i],:]
return centroids
init_centroids(X, 3)array([[3.18412176, 1.41410799],
[1.30882588, 5.30158701],
[1.95538864, 1.32156857]])
2.应用于图像压缩
这里需要暗转skimage,但直接安装会报错，需要先pip install scikit-image 这个需要等一段时间，之后再 pip install skimage，我的安装有问题。呜呜呜
from IPython.display import Image
Image(filename='E:/Python/machine learning/data/bird_small.png')
# 原始像素测像素点数值
image_data = loadmat('E:/Python/machine learning/data/bird_small.mat')
image_data{'__header__': b'MATLAB 5.0 MAT-file, Platform: GLNXA64, Created on: Tue Jun 5 04:06:24 2012',
'__version__': '1.0',
'__globals__': [],
'A': array([[[219, 180, 103],
[230, 185, 116],
[226, 186, 110],
...,
[ 14, 15, 13],
[ 13, 15, 12],
[ 12, 14, 12]],
[[230, 193, 119],
[224, 192, 120],
[226, 192, 124],
...,
[ 16, 16, 13],
[ 14, 15, 10],
[ 11, 14, 9]],
[[228, 191, 123],
[228, 191, 121],
[220, 185, 118],
...,
[ 14, 16, 13],
[ 13, 13, 11],
[ 11, 15, 10]],
...,
[[ 15, 18, 16],
[ 18, 21, 18],
[ 18, 19, 16],
...,
[ 81, 45, 45],
[ 70, 43, 35],
[ 72, 51, 43]],
[[ 16, 17, 17],
[ 17, 18, 19],
[ 20, 19, 20],
...,
[ 80, 38, 40],
[ 68, 39, 40],
[ 59, 43, 42]],
[[ 15, 19, 19],
[ 20, 20, 18],
[ 18, 19, 17],
...,
[ 65, 43, 39],
[ 58, 37, 38],
[ 52, 39, 34]]], dtype=uint8)}
A = image_data['A']
A.shape(128, 128, 3)
# 对数据应用一些预处理，并将其提供给K-means算法
# normalize value ranges
A = A / 255.
# reshape the array
X = np.reshape(A, (A.shape[0] * A.shape[1], A.shape[2]))
print(X.shape)
# randomly initialize the centroids
initial_centroids = init_centroids(X, 16)
# run the algorithm
idx, centroids = run_k_means(X, initial_centroids, 10)
# get the closest centroids one last time
idx = find_closest_centroids(X, centroids)
# map each pixel to the centroid value
X_recovered = centroids[idx.astype(int),:]
print(X_recovered.shape)
# reshape to the original dimensions
X_recovered = np.reshape(X_recovered, (A.shape[0], A.shape[1], A.shape[2]))
print(X_recovered.shape)
(16384, 3) (16384, 3) (128, 128, 3)
plt.imshow(X_recovered)
plt.show()
不知道为啥我运行出来就成黑的了
正常应该是这样的：
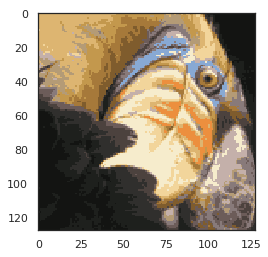
# 可以看到我们对图像进行了压缩，但图像的主要特征仍然存在
# 这就是K-means 下面我们来用scikit-learn来实现K-means
from skimage import io
# cast to float, you need to do this otherwise the color would be weird after clustring
pic = io.imread('E:/Python/machine learning/data/bird_small.png') / 255.
io.imshow(pic)
plt.show()
print(pic.shape)
# serialize data
data = pic.reshape(128*128, 3)
print(data.shape)
from sklearn.cluster import KMeans#导入kmeans库
model = KMeans(n_clusters=16, n_init=100, n_jobs=-1)
model.fit(data)(128, 128, 3)
(16384, 3)
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
n_clusters=16, n_init=100, n_jobs=-1, precompute_distances='auto',
random_state=None, tol=0.0001, verbose=0)
centroids = model.cluster_centers_
print(centroids.shape)
C = model.predict(data)
print(C.shape)
print(centroids[C].shape)
compressed_pic = centroids[C].reshape((128,128,3))
fig, ax = plt.subplots(1, 2)
ax[0].imshow(pic)
ax[1].imshow(compressed_pic)
plt.show()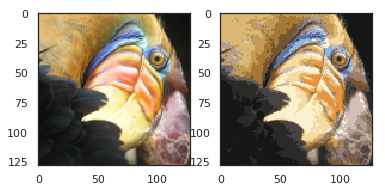
PCAex7
1.将PCA应用于一个简单的二维数据集
# PCA1
data = loadmat('E:/Python/machine learning/data/ex7data1.mat')
data{'__header__': b'MATLAB 5.0 MAT-file, Platform: PCWIN64, Created on: Mon Nov 14 22:41:44 2011',
'__version__': '1.0',
'__globals__': [],
'X': array([[3.38156267, 3.38911268],
[4.52787538, 5.8541781 ],
[2.65568187, 4.41199472],
[2.76523467, 3.71541365],
[2.84656011, 4.17550645],
[3.89067196, 6.48838087],
[3.47580524, 3.63284876],
[5.91129845, 6.68076853],
[3.92889397, 5.09844661],
[4.56183537, 5.62329929],
[4.57407171, 5.39765069],
[4.37173356, 5.46116549],
[4.19169388, 4.95469359],
[5.24408518, 4.66148767],
[2.8358402 , 3.76801716],
[5.63526969, 6.31211438],
[4.68632968, 5.6652411 ],
[2.85051337, 4.62645627],
[5.1101573 , 7.36319662],
[5.18256377, 4.64650909],
[5.70732809, 6.68103995],
[3.57968458, 4.80278074],
[5.63937773, 6.12043594],
[4.26346851, 4.68942896],
[2.53651693, 3.88449078],
[3.22382902, 4.94255585],
[4.92948801, 5.95501971],
[5.79295774, 5.10839305],
[2.81684824, 4.81895769],
[3.88882414, 5.10036564],
[3.34323419, 5.89301345],
[5.87973414, 5.52141664],
[3.10391912, 3.85710242],
[5.33150572, 4.68074235],
[3.37542687, 4.56537852],
[4.77667888, 6.25435039],
[2.6757463 , 3.73096988],
[5.50027665, 5.67948113],
[1.79709714, 3.24753885],
[4.3225147 , 5.11110472],
[4.42100445, 6.02563978],
[3.17929886, 4.43686032],
[3.03354125, 3.97879278],
[4.6093482 , 5.879792 ],
[2.96378859, 3.30024835],
[3.97176248, 5.40773735],
[1.18023321, 2.87869409],
[1.91895045, 5.07107848],
[3.95524687, 4.5053271 ],
[5.11795499, 6.08507386]])}
X = data['X']
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(X[:, 0], X[:, 1])
plt.show()
# PCA的算法相当简单。 在确保数据被归一化之后，输出仅仅是原始数据的协方差矩阵的奇异值分解
def pca(X):
# normalize the features
X = (X - X.mean()) / X.std()
# compute the covariance matrix
X = np.matrix(X)
cov = (X.T * X) / X.shape[0]
# perform SVD
U, S, V = np.linalg.svd(cov)
return U, S, V
U, S, V = pca(X)
U, S, V(matrix([[-0.79241747, -0.60997914],
[-0.60997914, 0.79241747]]),
array([1.43584536, 0.56415464]),
matrix([[-0.79241747, -0.60997914],
[-0.60997914, 0.79241747]]))
# 实现一个计算投影并且仅选择顶部K个分量的函数，有效地减少了维数
def project_data(X, U, k):
U_reduced = U[:,:k]
return np.dot(X, U_reduced)
Z = project_data(X, U, 1)
Z
matrix([[-4.74689738],
[-7.15889408],
[-4.79563345],
[-4.45754509],
[-4.80263579],
[-7.04081342],
[-4.97025076],
[-8.75934561],
[-6.2232703 ],
[-7.04497331],
[-6.91702866],
[-6.79543508],
[-6.3438312 ],
[-6.99891495],
[-4.54558119],
[-8.31574426],
[-7.16920841],
[-5.08083842],
[-8.54077427],
[-6.94102769],
[-8.5978815 ],
[-5.76620067],
[-8.2020797 ],
[-6.23890078],
[-4.37943868],
[-5.56947441],
[-7.53865023],
[-7.70645413],
[-5.17158343],
[-6.19268884],
[-6.24385246],
[-8.02715303],
[-4.81235176],
[-7.07993347],
[-5.45953289],
[-7.60014707],
[-4.39612191],
[-7.82288033],
[-3.40498213],
[-6.54290343],
[-7.17879573],
[-5.22572421],
[-4.83081168],
[-7.23907851],
[-4.36164051],
[-6.44590096],
[-2.69118076],
[-4.61386195],
[-5.88236227],
[-7.76732508]])
# 我们也可以通过反向转换步骤来恢复原始数据。
def recover_data(Z, U, k):
U_reduced = U[:,:k]
return np.dot(Z, U_reduced.T)
X_recovered = recover_data(Z, U, 1)
X_recoveredmatrix([[3.76152442, 2.89550838],
[5.67283275, 4.36677606],
[3.80014373, 2.92523637],
[3.53223661, 2.71900952],
[3.80569251, 2.92950765],
[5.57926356, 4.29474931],
[3.93851354, 3.03174929],
[6.94105849, 5.3430181 ],
[4.93142811, 3.79606507],
[5.58255993, 4.29728676],
[5.48117436, 4.21924319],
[5.38482148, 4.14507365],
[5.02696267, 3.8696047 ],
[5.54606249, 4.26919213],
[3.60199795, 2.77270971],
[6.58954104, 5.07243054],
[5.681006 , 4.37306758],
[4.02614513, 3.09920545],
[6.76785875, 5.20969415],
[5.50019161, 4.2338821 ],
[6.81311151, 5.24452836],
[4.56923815, 3.51726213],
[6.49947125, 5.00309752],
[4.94381398, 3.80559934],
[3.47034372, 2.67136624],
[4.41334883, 3.39726321],
[5.97375815, 4.59841938],
[6.10672889, 4.70077626],
[4.09805306, 3.15455801],
[4.90719483, 3.77741101],
[4.94773778, 3.80861976],
[6.36085631, 4.8963959 ],
[3.81339161, 2.93543419],
[5.61026298, 4.31861173],
[4.32622924, 3.33020118],
[6.02248932, 4.63593118],
[3.48356381, 2.68154267],
[6.19898705, 4.77179382],
[2.69816733, 2.07696807],
[5.18471099, 3.99103461],
[5.68860316, 4.37891565],
[4.14095516, 3.18758276],
[3.82801958, 2.94669436],
[5.73637229, 4.41568689],
[3.45624014, 2.66050973],
[5.10784454, 3.93186513],
[2.13253865, 1.64156413],
[3.65610482, 2.81435955],
[4.66128664, 3.58811828],
[6.1549641 , 4.73790627]])
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(list(X_recovered[:, 0]), list(X_recovered[:, 1]))
plt.show()
# 注意，第一主成分的投影轴基本上是数据集中的对角线。 当我们将数据减少到一个维度时，我们失去了该对角线周围的变化，
# 所以在我们的再现中，一切都沿着该对角线
2.将PCA应用于脸部图像
faces = loadmat('E:/Python/machine learning/data/ex7faces.mat')
X = faces['X']
X.shape(5000, 1024)
def plot_n_image(X, n):
""" plot first n images
n has to be a square number
"""
pic_size = int(np.sqrt(X.shape[1]))
grid_size = int(np.sqrt(n))
first_n_images = X[:n, :]
fig, ax_array = plt.subplots(nrows=grid_size, ncols=grid_size,
sharey=True, sharex=True, figsize=(8, 8))
for r in range(grid_size):
for c in range(grid_size):
ax_array[r, c].imshow(first_n_images[grid_size * r + c].reshape((pic_size, pic_size)))
plt.xticks(np.array([]))
plt.yticks(np.array([]))
face = np.reshape(X[3,:], (32, 32))
plt.imshow(face)
plt.show()
# 看起来很糟糕。 这些只有32 x 32灰度的图像（它也是侧面渲染，但我们现在可以忽略）。 我们的下一步是在面数据集上运行PCA，并取得前100个主要特征。
U, S, V = pca(X)
Z = project_data(X, U, 100)
# 现在我们可以尝试恢复原来的结构并再次渲染。
X_recovered = recover_data(Z, U, 100)
face = np.reshape(X_recovered[3,:], (32, 32))
plt.imshow(face)
plt.show()
# 注意，我们失去了一些细节，尽管没有像您预期的维度数量减少10倍 
1948
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
