机器学习数学原理专题——回归模型：损失函数推导

目录

一、从线性模型开始：回归

1.回归模型

        (1)基本形式

        (2)代数形式

2.回归模型损失函数的推导

     （1）感性直觉（最小二乘法）

      （2）理性推导（极大似然估计法）

---

一、从线性模型开始：回归

---

1.回归模型

        (1)基本形式

              线性模型基本表示为   

        其中y为预测变量，在回归问题中可以理解为想要预测的响应变量，如股票未来价格、预测房价、预测个人可能工资等；

       x为特征变量，是用于训练模型的核心数据，代表了对问题现实描述的影响因子，如股票价格预测中的股市技术指标、房价影响因素中的房屋面积，楼层数，过往成交价格等、个人工资中个人学历，年龄，性别等。对于现实中的任务，其结果的影响因素可能很多，此处假设存在n个影响因子x；

      w为模型参数，可以理解为每个影响因子x对预测值y的重要程度，是权值参数，如股票短期预测中是技术指标更重要，还是宏观因素更重要；影响房价的众多因素中，房屋面积是不是占主要地位；个人工资又是不是大部分由个人学历决定。对于这些问题的回答，将决定对应影响因子前的权值大小。

      为误差项，误差项代表了数据的随机性和不可预测性，是数据中的噪音。可能包括测量误差、数据收集过程中的误差，或是模型未能包含的其他变量的影响。

        (2)代数形式

             线性模型代数表示为                     

                      其中，                  ,

            在代数模型中，将误差项加入了特征矩阵中，是为了简化了模型表达，本质上和基本形式是一样的。

2.回归模型损失函数的推导

        模型的预测值 和实际样本的观测值 。上述构建的线性回归模型将样本的特征变量 以权重参数 的方式求和，得到模型的预测结果  。实际机器学习中有一个训练模型的过程，此时还需要对预测结果进行评估，这就需要一个“标准答案”，这就是样本的观测实际值 。

        为了训练回归的模型参数，需要一个度量训练输出 和实际数据   “差异”的函数，这就是损失函数。损失函数在机器学习中发挥关键作用，就如同我们学习过程中对我们学习现状（做试卷）打分的“老师”一样。

        损失函数更像是一个“文科老师”（不同于数学结果只有对错一种评判结果），损失函数的“打分方式”可以有很多，一个好的评分方式对我们学习很重要（比如如果政治主观题只以字数多少作为得分标准显然不合适），因此选择合适的损失函数形式在机器学习过程中很重要。

     （1）感性直觉（最小二乘法）

         均方误差MSE (Mean Squared Error），是回归任务常用的损失函数。通过回归模型的基本形式可知，模型中存在一个误差项，既是数学模型无法解释实际观测值的部分，也是模型预测值和实际值的差距（欧式距离）。

                                  

                                     

       误差项表示观测值和模型预测值的差异，最小二乘法MSE旨在最小化所有误差项的平方和。这个误差就是下图中样本点到预测线的绿色虚线距离，MSE就是要找到一条这样的线，使得所有样本点到线性直线上对应点的距离和最小。

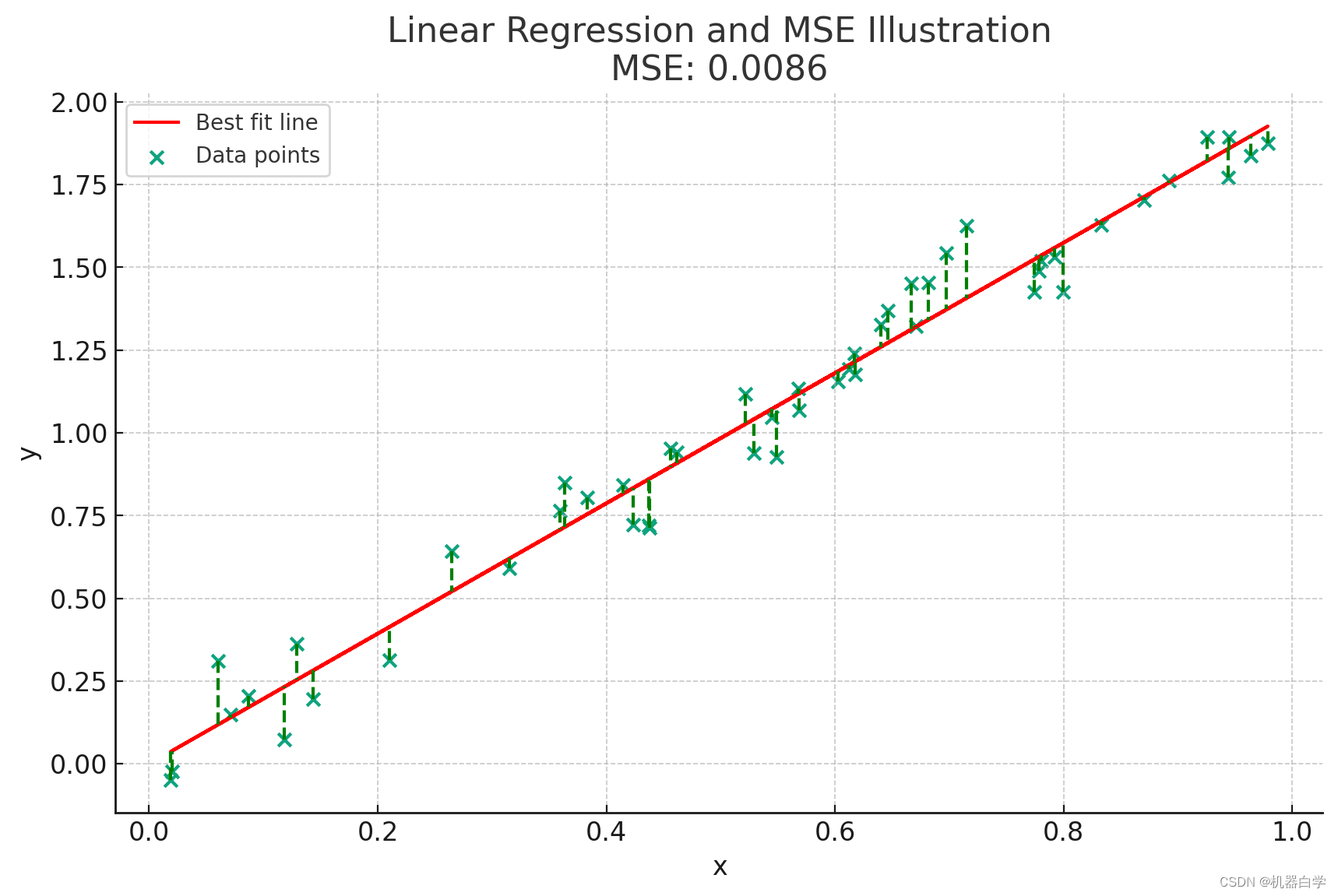
       上述内容用数学表示如下。

                                                      

                          

       在损失函数输入的所有变量中， 都为观测固定，只有参数 可变。取平方是为了防止数值的正负相消。

       在实际中，损失函数作为度量模型表现的测度，更关心的是相对值，而不是绝对大小。因此常常对上述所有样本的和再取平均值。下式中 是总共样本的个数。

                            

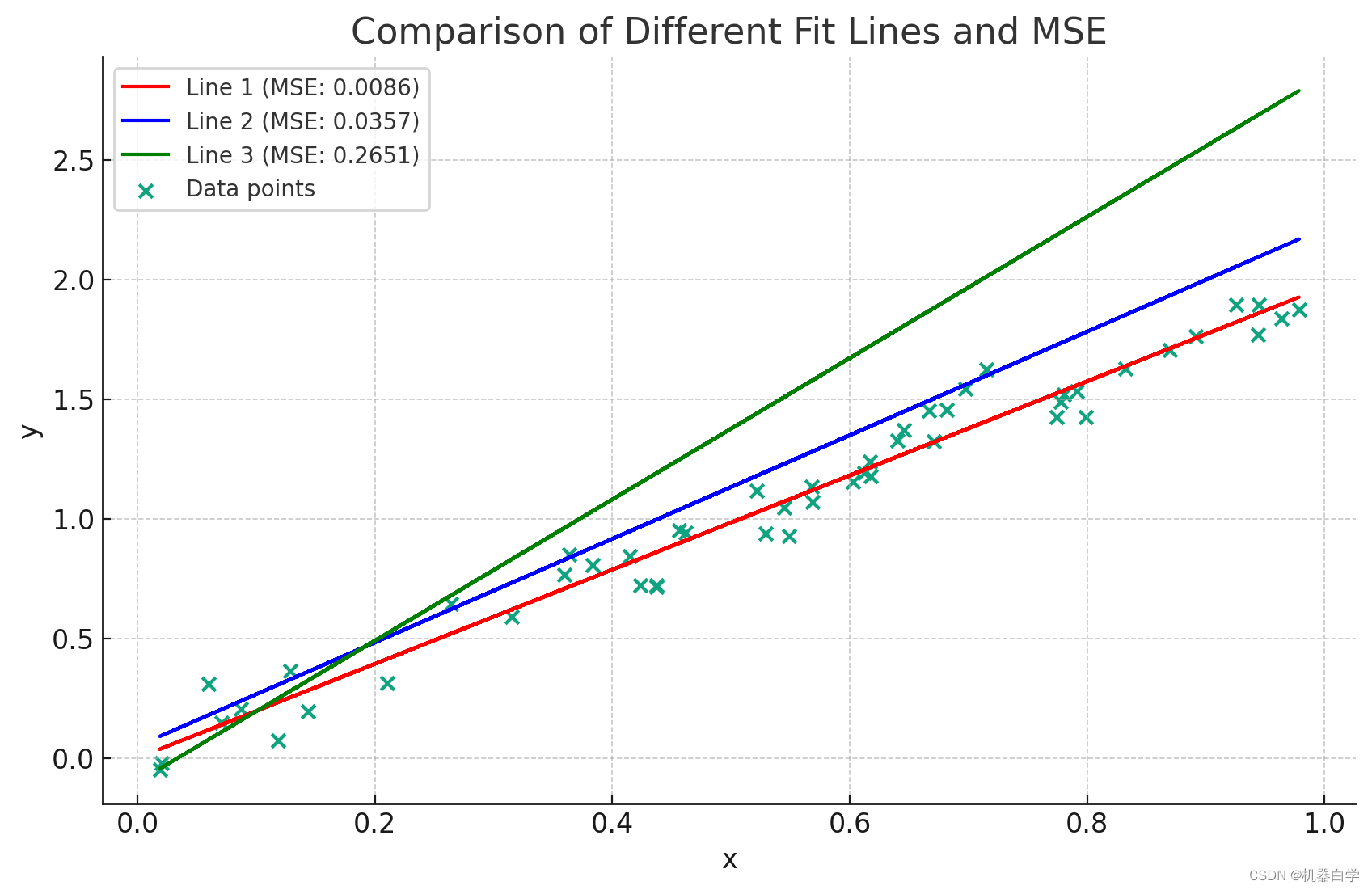
       下图展示了找到最优曲线的一种过程，可以看到和样本点“拟合”程度最高的红色曲线，对应的损失函数MSE取值也最小。因此最小化损失函数以找到最优曲线的方法，至少看上去是十分合理有效的。