ICLR2018 | PGD | 迈向抵御对抗攻击的深度学习模型

四口鲸鱼爱吃盐

已于 2025-02-25 10:50:32 修改

阅读量1.7k

点赞数 15

分类专栏：文献阅读文章标签：深度学习人工智能计算机视觉对抗样本

于 2025-01-01 10:36:59 首次发布

本文链接：https://blog.csdn.net/qq_60090693/article/details/144861850

版权

文献阅读专栏收录该内容

107 篇文章

订阅专栏

Towards Deep Learning Models Resistant to Adversarial Attacks

摘要
Introduction-引言
对抗鲁棒性的优化视角-An Optimization View on Adversarial Robustness
迈向通用鲁棒网络-Towards Universally Robust Networks
实验: 对抗鲁棒的深度学习模型-Experiments: Adversarially Robust Deep Learning Models
相关工作-Related Work
结论-Conclusion

论文链接

本文 “Towards Deep Learning Models Resistant to Adversarial Attacks” 通过稳健优化方法研究神经网络对抗攻击的鲁棒性，提出用鞍点（最小 - 最大）公式精确描述对抗攻击的安全性，为攻击和防御构建统一理论框架，训练出对多种对抗攻击有高抗性的模型，推动深度学习模型在对抗攻击方面的安全性研究

摘要

Recent work has demonstrated that deep neural networks are vulnerable to adversarial examples—inputs that are almost indistinguishable from natural data and yet classified incorrectly by the network. In fact, some of the latest findings suggest that the existence of adversarial attacks may be an inherent weakness of deep learning models. To address this problem, we study the adversarial robustness of neural networks through the lens of robust optimization. This approach provides us with a broad and unifying view on much of the prior work on this topic. Its principled nature also enables us to identify methods for both training and attacking neural networks that are reliable and, in a certain sense, universal. In particular, they specify a concrete security guarantee that would protect against any adversary. These methods let us train networks with significantly improved resistance to a wide range of adversarial attacks. They also suggest the notion of security against a first-order adversary as a natural and broad security guarantee. We believe that robustness against such well-defined classes of adversaries is an important stepping stone towards fully resistant deep learning models.

近期的研究表明，深度神经网络容易受到对抗样本的攻击——这些输入与自然数据几乎无法区分，但却被网络错误分类。事实上，一些最新的研究结果表明，对抗攻击的存在可能是深度学习模型的一个固有弱点。为了解决这个问题，我们从鲁棒优化的角度研究神经网络的对抗鲁棒性。这种方法为我们提供了一个广泛而统一的视角，涵盖了该主题的许多先前工作。其原则性本质还使我们能够确定用于训练和攻击神经网络的方法，这些方法是可靠的，并且在某种意义上是通用的。特别是，它们指定了一个具体的安全保证，可以防范任何对抗攻击。这些方法使我们能够训练出对广泛的对抗攻击具有显著提高的抗性的网络。它们还提出了针对一阶对抗攻击的安全性概念，作为一种自然而广泛的安全保证。我们认为，针对此类明确界定的对抗攻击类别的鲁棒性是迈向完全抗性的深度学习模型的重要一步。

Introduction-引言

该部分主要介绍了深度学习模型面临的对抗攻击问题，引出通过鲁棒优化研究对抗鲁棒性的方法，具体内容如下：

研究背景
- 深度学习模型的广泛应用与安全问题：计算机视觉和自然语言处理领域的突破使训练分类器在安全关键系统中愈发重要，如自动驾驶汽车视觉、人脸识别和恶意软件检测等。然而，尽管训练模型在分类良性输入时有效，但容易受到对抗样本攻击，即输入微小变化可导致模型误分类，这不仅影响安全，还表明模型未稳健学习底层概念，引发如何训练鲁棒神经网络的问题。
- 对抗攻击研究现状与不足：已有大量工作提出各种对抗攻击和防御机制，但这些工作对其提供的保证缺乏深入理解，难以评估和应对对抗鲁棒性问题。
研究方法
- 优化视角的引入：从优化角度研究对抗鲁棒性，考虑标准分类任务，目标是最小化风险，但经验风险最小化（ERM）得到的模型常对对抗样本脆弱。
- 攻击模型与鞍点问题定义
  - 攻击模型：引入允许扰动集 $S$ （如 $\ell_{\infty}$ - 球）定义对抗鲁棒性，用于形式化对抗攻击操纵能力。
  - 鞍点问题：修改总体风险定义，得到鞍点问题 $\min _{\theta} \rho(\theta)$ （ $\rho(\theta)=\mathbb{E}_{(x, y) \sim \mathcal{D}}\left[\max _{\delta \in \mathcal{S}} L(\theta, x+\delta, y)\right]$ ），内部最大化问题是攻击神经网络，外部最小化问题是训练鲁棒分类器，此视角统一了先前对抗鲁棒性相关工作。
研究贡献
- 从优化角度研究对抗鲁棒性，用鞍点问题表述，涵盖先前工作，明确理想鲁棒分类器目标和定量鲁棒性度量。
- 提出通过鲁棒优化训练鲁棒神经网络，确定PGD为“通用”一阶对抗攻击，训练网络对多种攻击有显著抗性，为实现完全抗性模型提供重要思路。

对抗鲁棒性的优化视角-An Optimization View on Adversarial Robustness

该部分主要从优化视角深入剖析对抗鲁棒性，阐述了相关的理论基础、与先前工作的联系以及对后续研究的启示，具体内容如下：

优化视角的理论阐述
- 标准分类任务与风险最小化目标
  - 以标准分类任务为背景，涉及数据分布 $D$ （包含示例 $x$ 和标签 $y$ ）以及损失函数 $L(\theta, x, y)$ ，通常目标是通过最小化 $\mathbb{E}_{(x, y) \sim D}[L(x, y, \theta)]$ 来寻找最优模型参数 $\theta$ .
  - 然而，经验风险最小化（ERM）在面对对抗样本时存在缺陷，无法确保模型的鲁棒性。
- 引入攻击模型与鞍点问题
  - 为解决上述问题，引入攻击模型，通过定义允许扰动集 $S$ （如 $\ell_{\infty}$ - 球）来描述对抗攻击的操纵能力，从而将对抗因素纳入考量。
  - 基于此，提出鞍点问题 $\min _{\theta} \rho(\theta)$ （其中 $\rho(\theta)=\mathbb{E}_{(x, y) \sim \mathcal{D}}\left[\max _{\delta \in \mathcal{S}} L(\theta, x+\delta, y)\right]$ ）。该问题的内部最大化旨在寻找能使损失最大的对抗样本（对应攻击神经网络），外部最小化则是为了找到使内部攻击问题的 “对抗损失” 最小的模型参数（即训练鲁棒分类器）。
统一先前工作的视角
- 攻击方法的解读
  - 前人提出的攻击方法，如Fast Gradient Sign Method（FGSM）及其变体，可视为解决鞍点问题内部最大化问题的尝试。FGSM通过 $x+\varepsilon sgn\left(\nabla_{x} L(\theta, x, y)\right)$ 计算对抗样本，是一种简单的一步攻击方案；而多步变体（如PGD）则是在负损失函数上进行投影梯度下降，具有更强的攻击能力。
- 防御机制的分析
  - 训练防御机制中，用FGSM生成的对抗样本扩充训练数据集的方法，可看作是在解决简化的鲁棒优化问题时，对内部最大化问题的一种近似处理。更复杂的防御机制（如训练对抗多个对抗攻击）则是对内部最大化问题更好的近似。
对后续研究的意义
- 这种优化视角为研究对抗鲁棒性提供了一个统一的框架，将攻击和防御方法纳入共同的理论体系中，有助于深入理解对抗样本的产生和防御原理。
- 为后续研究提供了明确的方向，如通过解决鞍点问题来实现鲁棒分类器的训练，以及探索更有效的攻击和防御方法。同时，也为评估模型的对抗鲁棒性提供了定量的依据，即通过最小化鞍点问题中的风险来衡量模型的鲁棒性程度。

迈向通用鲁棒网络-Towards Universally Robust Networks

对抗样本的损失景观-The Landscape of Adversarial Examples

内部问题的可处理性探讨
- 内部问题是为给定网络和数据点找到对抗样本（受攻击模型约束），由于需最大化一个高度非凹函数，是被认为棘手的。先前工作常通过线性化内部最大化问题来处理，如FGSM就是这种方法的产物，但FGSM作为一步攻击方法存在局限性，更复杂的对抗攻击仍可找到高损失点。
实验方法与现象观察
- 实验使用投影梯度下降（PGD）探索MNIST和CIFAR10数据集上多个模型的局部最大值情况，通过从数据点周围 $\ell_{\infty}$ 球内的许多点重新启动PGD来探索损失景观。
- 实验发现，从 $x + S$ 内随机选择起始点执行投影 $\ell_{\infty}$ 梯度下降时，对抗损失以相当一致的方式增加并迅速趋于平稳（见图1）。
- 对最大值的集中性进一步研究发现，经过大量随机重启，最终迭代的损失遵循集中分布，无极端异常值（见图2）。通过测量局部最大值之间的 $\ell_{2}$ 距离和角度，发现它们明显不同，距离分布接近 $\ell_{\infty}$ 球内两个随机点的预期距离，角度接近90°，且沿局部最大值之间的线段，损失是凸的，在端点处达到最大值，中间降低，但整个线段的损失仍高于随机点。
- 还观察到最大值的分布表明，近期对抗样本的子空间观点未完全捕捉攻击的丰富性，存在与示例梯度内积为负的对抗扰动，且随着扰动规模增加，与梯度方向的相关性恶化。

在这里插入图片描述
图1：从MNIST和CIFAR10评估数据集中创建对抗样本时的交叉熵损失值。这些图展示了在20次投影梯度下降（PGD）运行过程中损失是如何演变的。每次运行都从同一自然样本周围的 $\ell_{\infty}$ 球内的均匀随机点开始（不同示例的额外图见图11）。经过少量迭代后，对抗损失趋于平稳。优化轨迹和最终损失值也相当集中，特别是在CIFAR10上。此外，经过对抗训练的网络的最终损失值明显小于其标准对应网络的损失值.

在这里插入图片描述
图2：来自MNIST和CIFAR10评估数据集的五个示例的交叉熵损失给出的局部最大值的值。对于每个示例，我们从示例周围的 $\ell_{\infty}$ 球内的105个均匀随机点开始投影梯度下降（PGD），并迭代PGD直到损失趋于平稳。蓝色直方图对应于标准网络上的损失，而红色直方图对应于经过对抗训练的网络。经过对抗训练的网络的损失明显更小，并且最终损失值非常集中，没有任何异常值.

结论与意义
- 这些现象表明，至少从一阶方法的角度来看，内部问题是可处理的，PGD找到的局部最大值损失值相似，这为后续将PGD视为“通用”一阶对抗攻击的讨论提供了基础，为研究对抗鲁棒性提供了新的视角，对理解对抗样本的生成和防御具有重要意义。

一阶对抗攻击-First-Order Adversaries

该部分主要阐述了基于实验现象对一阶对抗攻击的分析与猜想，探讨了PGD作为“通用”一阶对抗攻击方法的合理性，以及模型对PGD攻击的鲁棒性在不同攻击场景下的意义，具体内容如下：

PGD攻击下的损失集中现象：实验表明，无论是正常训练还是对抗训练的网络，PGD找到的局部极大值损失值都相似。这一集中现象表明，对PGD攻击具有鲁棒性，可能意味着对所有仅依赖一阶信息的攻击都具有鲁棒性。因为只要攻击者仅使用损失函数相对于输入的梯度，就不太可能找到比PGD更好的局部极大值。
PGD作为“通用”一阶对抗攻击的依据：虽然不排除存在孤立的、函数值大得多的极大值，但实验发现用一阶方法很难找到它们。即便大量随机重启PGD，也未发现损失值有显著差异的函数值。在机器学习中，多数优化问题用一阶方法求解，随机梯度下降（SGD）的变体是训练深度学习模型的有效方式。因此，依赖一阶信息的攻击在某种意义上对当前深度学习实践具有普遍性，PGD可被视为“通用”的一阶对抗攻击方法。
模型鲁棒性在不同攻击场景下的体现：如果训练网络对PGD攻击具有鲁棒性，它将对包括当前所有方法在内的广泛攻击具有鲁棒性。在黑盒攻击场景中，这种鲁棒性保证会更强。因为黑盒攻击中，攻击者无法直接访问目标网络，只能获取有限信息，可看作“零阶”攻击。增加网络容量和强化训练时对抗的对手（如采用FGSM或PGD训练而非标准训练），能够提高模型对迁移攻击的抵抗力，且最佳模型对这类攻击的抵抗力明显强于对最强一阶攻击的抵抗力。

对抗训练的下降方向-Descent Directions for Adversarial Training

内部优化与外部优化的关系
- 内部优化问题可通过PGD解决，而训练对抗鲁棒网络还需解决鞍点公式（2.1）的外部优化问题，即找到使“对抗损失”（内部最大化问题的值）最小化的模型参数。
计算外部问题梯度的方法与理论依据
- 计算外部问题 $\nabla_{\theta} \rho(\theta)$ 梯度的自然方法是计算内部问题最大值处的损失函数梯度，这相当于用对抗扰动替换输入点后正常训练网络。对于连续可微函数，Danskin定理表明内部最大化问题的梯度对应于鞍点问题的下降方向。
实际情况与实验验证
- 虽然Danskin定理假设不完全适用于该问题（因神经网络中ReLU和最大池化单元使函数非连续可微，且仅计算内部问题近似最大值），但实验发现用对抗样本处损失梯度应用SGD可降低鞍点问题损失（见图5），表明能可靠优化鞍点公式，训练出鲁棒分类器。

网络容量与对抗鲁棒性-Network Capacity and Adversarial Robustness

网络容量对鲁棒分类的重要性阐述
- 解决优化问题（公式2.1）只是第一步，还需保证对抗样本的最终损失值小，才能确保分类器性能良好。对抗样本改变了决策边界，使其更复杂，所以需要更强（即更大容量）的分类器来实现稳健分类（图3）。

在这里插入图片描述
图3：标准决策边界与对抗决策边界的概念性图示。
左图：一组可以用简单（在此情况下为线性）决策边界轻松分离的点。
中图：简单决策边界无法分离数据点周围的 $\ell_{\infty}$ - 球（此处为正方形）。因此存在会被错误分类的对抗样本（红色星号）。
右图：分离 $\ell_{\infty}$ - 球需要一个明显更复杂的决策边界。由此产生的分类器对具有有界 $\ell_{\infty}$ - 范数扰动的对抗样本具有鲁棒性.

MNIST数据集上的实验及发现
- 实验设置与网络结构变化：使用简单卷积网络，通过翻倍网络规模（卷积滤波器数量和全连接层大小）研究其对不同对抗攻击的行为变化。初始网络结构为含2个和4个滤波器的卷积层、64单元全连接隐藏层及2×2最大池化层，构建对抗样本时 $\varepsilon = 0.3$ .
- 不同训练方式下的性能表现
  - 自然样本训练：仅用自然样本训练时，容量增加使自然样本准确率提高，对较小 $\varepsilon$ 的一步扰动（如FGSM攻击）鲁棒性增强，说明容量提升有助于模型捕捉更多数据特征，增强对简单对抗攻击的防御。
  - FGSM对抗样本训练：用FGSM对抗样本训练会导致网络过拟合（标签泄漏），在自然样本上性能差且对PGD对抗攻击不鲁棒，因为FGSM产生的对抗样本有限，网络过度适应这些特定样本，缺乏泛化能力。
  - PGD对抗样本训练：小容量网络对抗PGD对抗攻击时，可能无法学习有效分类器，会收敛到固定类别预测，牺牲自然样本性能来换取有限对抗鲁棒性，无法平衡两者关系。
- 容量与其他因素的关系
  - 固定对抗攻击训练时，鞍点问题值随容量增加而降低，表明模型能更好拟合对抗样本，体现容量对降低对抗损失、提高鲁棒性的重要性。
  - 增加容量或使用更强对抗攻击可降低对抗样本转移性，通过计算源网络和转移网络在大量输入示例上损失函数梯度的角度分布，发现容量增加使梯度相关性降低，对抗样本在不同网络间有效性降低，减轻了实际应用中的对抗攻击威胁。
CIFAR10数据集上的实验及结论
- 实验设置与网络调整：采用ResNet模型，通过数据增强（随机裁剪、翻转和图像标准化）及修改网络结构（增加层宽10倍，形成特定滤波器数量的5个残差单元网络）来提高容量，构建对抗样本时 $\varepsilon = 8$ .
- 容量对性能和转移性的影响
  - 与MNIST实验类似，容量增加在不同训练方式（自然、FGSM对抗、PGD对抗训练）下对网络性能有积极影响，如自然样本准确率提升、对抗鲁棒性增强等。
  - 研究对抗样本转移性发现，更强对抗攻击（PGD训练）降低转移攻击成功率，增加网络容量（从简单架构到宽架构）也有助于降低转移性，从不同对抗数据集转移攻击时效果更明显，再次证明网络容量和训练对抗攻击强度对转移性的重要影响，且与MNIST实验结论呼应，表明相关规律具有一定普遍性。

在这里插入图片描述
图4：网络容量对网络性能的影响。我们在以下情况下训练了不同容量的MNIST和CIFAR10网络：
a: 自然样本;
b: 使用FGSM生成的对抗样本;
c: 使用PGD生成的对抗样本.
在每个数据集的前三个图/表中，我们展示了在每种训练机制下，标准准确率和对抗准确率如何随容量变化。在最后一个图/表中，我们展示了网络在其上进行训练的对抗样本的交叉熵损失值。这对应于我们的鞍点公式（2.1）对于不同允许扰动集的值。

实验: 对抗鲁棒的深度学习模型-Experiments: Adversarially Robust Deep Learning Models

训练方法与对抗攻击选择依据
- 根据前文研究，训练鲁棒分类器需关注两个关键要素：高容量网络和强对抗攻击。对于MNIST和CIFAR10数据集，选择投影梯度下降（PGD）作为对抗攻击，从自然样本周围随机扰动开始。训练时采用多轮训练，每轮遇到样本时选择新的随机扰动，而非多次重启PGD。实验观察到训练过程中对抗损失稳步下降，表明成功解决原始优化问题。

在这里插入图片描述
图5：训练期间对抗样本的交叉熵损失。这些图展示了在针对投影梯度下降（PGD）对抗攻击训练MNIST和CIFAR10网络时，训练样本的对抗损失是如何演变的。CIFAR10图中的急剧下降对应于训练步长的减小。这些图说明我们能够持续降低鞍点公式（2.1）内部问题的值，从而产生一个越来越鲁棒的分类器.

MNIST实验结果详情
- 网络结构与训练准确率：使用特定结构网络（两个卷积层分别有32和64个滤波器，后接2×2最大池化，再连接1024单元的全连接层），用自然样本训练时在评估集上准确率达99.2%，但用FGSM评估时准确率降至6.4%。
- 对抗不同对抗攻击的性能表现
  - 对抗多种 $\ell_{\infty}$ 有界对抗攻击时，网络表现出鲁棒性。对不同迭代和重启次数的PGD攻击，准确率有所变化，如40次迭代、1次重启时准确率为93.2%，100次迭代、1次重启时为91.8%等。对黑盒攻击（如来自独立训练网络、仅用自然样本训练的同一网络版本以及不同卷积架构的网络）准确率较高，对某些攻击（如CW+）也有一定抗性。
  - 对 $\ell_{2}$ 有界攻击，PGD在较大 $\varepsilon$ 值（如 $\varepsilon = 4.5$ ）时无法找到对抗样本，但后续研究表明PGD高估了模型的 $\ell_{2}$ 鲁棒性，不过 $\ell_{\infty}$ 训练的模型仍比标准模型对 $\ell_{2}$ 攻击更鲁棒。
- 模型参数分析：对训练后的MNIST模型参数分析发现，第一个卷积层学习到阈值输入像素（仅3个滤波器且每个滤波器仅1个权重非零，卷积退化为图像缩放和阈值操作），第二层滤波器权重稀疏且范围宽，与第一层的3个通道相关，软max层权重在不同网络版本中相似，但对抗训练网络的类偏差差异大且相似，表明网络通过调整偏差对易受攻击的类更保守预测，且这些特性是通过对抗训练学习到的，手动引入未成功。

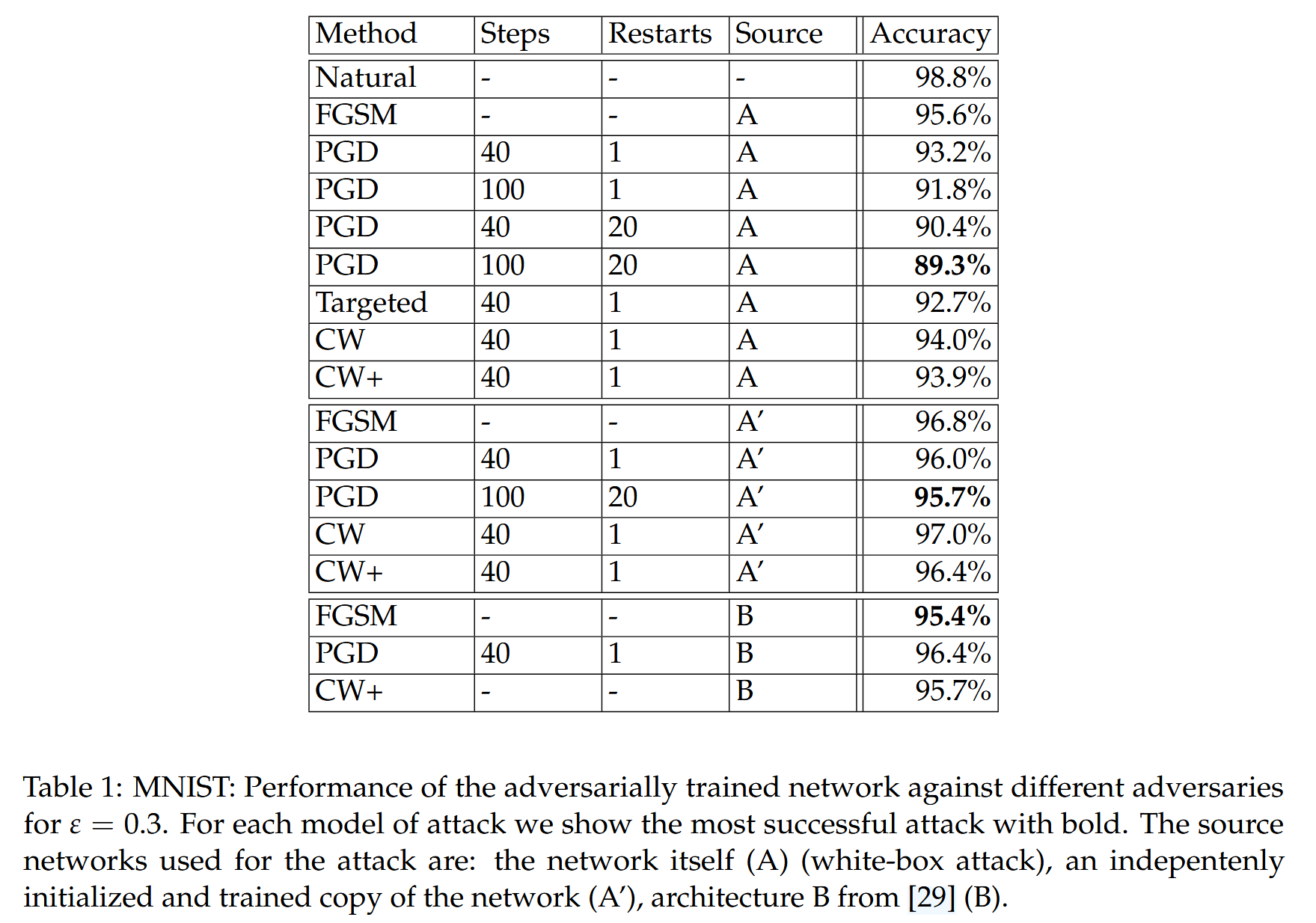
在这里插入图片描述
表1:MNIST： $ε = 0.3$ 时，对抗训练网络对不同对抗攻击的性能。对于每种攻击模式，我们都会用粗体显示最成功的攻击。用于攻击的源网络是：网络本身（ $A$ ）（白盒攻击），网络的独立初始化和训练副本（ $A^{'}$ ），[29]中的架构B（ $B$ ）。

CIFAR10实验结果展示
- 使用ResNet模型及其10倍宽变体，经PGD对抗攻击训练后，网络对迭代对抗攻击有一定鲁棒性，如7步PGD攻击时准确率为50.0%，20步时为45.8%，但与理想状态仍有差距，相信通过进一步增加网络容量等探索可提升性能。

在这里插入图片描述
表2:CIFAR10： $ε = 8$ 时，对抗训练网络对不同对抗攻击的性能。对于每种攻击模式，我们以粗体显示最有效的攻击。被考虑用于攻击的源网络是：网络本身（ $A$ ）（白盒攻击），独立初始化和训练的网络副本（ $A^{'}$ ），在自然样本上训练的网络的副本（ $A_{nat}$ ）。
4. 额外实验结果分析

为更全面评估模型对抗鲁棒性，进行了两个额外实验。一是研究对不同 $\varepsilon$ 值的 $\ell_{\infty}$ 有界攻击的抗性，发现小于训练 $\varepsilon$ 值时模型准确率如预期般相等或更高，MNIST模型在稍大 $\varepsilon$ 值时鲁棒性下降明显（可能因阈值算子调谐问题），CIFAR10模型衰减较平滑。二是检查模型对 $\ell_{2}$ 有界攻击的抗性，MNIST模型中PGD在较大 $\varepsilon$ 值下表现异常（无法找到对抗样本但实际可能不鲁棒），后续研究证实PGD高估其 $\ell_{2}$ 鲁棒性，不过 $\ell_{\infty}$ 训练模型仍更抗 $\ell_{2}$ 攻击。

在这里插入图片描述
图6：我们经过对抗训练的网络针对不同强度的PGD对抗攻击的性能表现。MNIST和CIFAR10网络分别针对 $\varepsilon = 0.3$ 和 $\varepsilon = 8$ 的PGD $\ell_{\infty}$ 对抗攻击进行训练（训练 $\varepsilon$ 在 $\ell_{\infty}$ 图中用红色虚线表示）。对于经过对抗训练的MNIST网络，我们还评估了决策边界攻击（DBA）在标准模型和对抗训练模型上进行2000步的性能以及PGD的性能。我们观察到，当 $\varepsilon$ 小于或等于训练期间使用的值时，性能相等或更好。对于MNIST，在稍大 $\varepsilon$ 值后不久性能急剧下降。此外，我们观察到在MNIST $\ell_{2}$ 训练的网络上PGD的性能较差，并且明显高估了模型的鲁棒性。这可能是由于模型学习到的阈值滤波器掩盖了损失梯度（基于决策的攻击不使用梯度）.

结论-Conclusion

研究成果回顾
- 从鲁棒优化角度对对抗鲁棒性展开研究，将诸多关于对抗鲁棒性的前期工作通过鞍点问题的形式进行了统一表述，为该领域提供了一个较为宽泛且整合性的视角。
- 经过实验探索，发现内部最大化问题（对应寻找对抗样本）有着相对易于处理的局部最大值结构，这一发现很关键，并且据此提出可将投影梯度下降（PGD）视为一种“通用”的一阶对抗攻击。
- 通过利用上述成果开展对抗训练，能够训练出对各式各样对抗攻击具备显著更强抗性的网络，比如在MNIST和CIFAR10数据集上的实验都展现出良好的鲁棒性表现。
对未来研究的展望
- 强调尽管当前研究取得了一定进展，但距离实现完全抗对抗攻击的深度学习模型还有很长的路要走，仍有诸多挑战需要攻克。
- 指出未来研究可聚焦于进一步提升网络的对抗鲁棒性，探索更有效的训练方法、优化网络架构等方面，朝着构建出完全能抵御对抗攻击的深度学习模型这一目标持续迈进。