ICLR2021 | IR | 一种解释和提高对抗性迁移能力的统一方法

---

原文链接

本文 “A Unified Approach To Interpreting And Boosting Adversarial Transferability” 从对抗扰动内部交互的角度，解释对抗样本的可迁移性，并提出新方法提升其可迁移性。

---

摘要-Abstract

In this paper, we use the interaction inside adversarial perturbations to explain and boost the adversarial transferability. We discover and prove the negative correlation between the adversarial transferability and the interaction inside adversarial perturbations. The negative correlation is further verified through different DNNs with various inputs. Moreover, this negative correlation can be regarded as a unified perspective to understand current transferability-boosting methods. To this end, we prove that some classic methods of enhancing the transferability essentially decease interactions inside adversarial perturbations. Based on this, we propose to directly penalize interactions during the attacking process, which significantly improves the adversarial transferability.

在本文中，我们利用对抗扰动内部的相互作用来解释和提升对抗样本的可迁移性。我们发现并证明了对抗样本的可迁移性与对抗扰动内部的相互作用之间存在负相关关系。这种负相关关系通过不同的深度神经网络（DNN）和各种输入进一步得到验证。此外，这种负相关关系可以被视为理解当前提升可迁移性方法的统一视角。为此，我们证明了一些经典的提升可迁移性的方法本质上是减少了对抗扰动内部的相互作用。基于此，我们提出在攻击过程中直接惩罚相互作用，这显著提高了对抗样本的可迁移性。

---

引言-Introduction

该部分主要介绍研究背景、创新视角、研究发现及验证、提出方法和研究贡献，具体内容如下：

1. 研究背景：近年来，深度神经网络（DNNs）的对抗样本备受关注，其扰动的可迁移性被发现后，虽有诸多方法试图增强可迁移性，但提升本质尚不明晰。
2. 创新视角：将对抗扰动内部的相互作用视为解释对抗样本可迁移性的新视角，利用博弈论中的Shapley交互指数定义这种相互作用。具体来说，给定输入样本 $x$，对抗攻击旨在添加不可察觉的扰动 $\delta$ 误导DNN。用Shapley值衡量扰动单元 ${\delta }_i$ 的重要性 ${\varphi }_i$，${\delta }_i$ 和 ${\delta }_j$ 之间的相互作用定义为 ${\delta }_j$ 扰动时 ${\varphi }_i$ 相较于 ${\delta }_j$ 未扰动时的变化。
3. 研究发现及验证：发现并部分证明了对抗样本可迁移性与对抗扰动单元间相互作用呈负相关，即可迁移性低的对抗扰动，其扰动单元间相互作用往往更大。通过理论证明和对比研究对该相关性进行了验证。
4. 提出方法：基于上述相关性，提出在攻击过程中惩罚相互作用以提升可迁移性，即通过引入一个新的损失函数来减少扰动单元间的相互作用。
5. 研究贡献：揭示了对抗样本可迁移性与对抗扰动内部相互作用的负相关关系；为理解现有提升可迁移性的方法提供统一视角；提出新的损失函数，通过惩罚对抗扰动内部的相互作用，有效提升了对抗样本的可迁移性。

---

相关工作-Related Work

该部分主要介绍了对抗可迁移性和交互两方面的相关研究，具体内容如下：

1. 对抗可迁移性：攻击方法分为白盒攻击和黑盒攻击，基于对抗可迁移性的黑盒攻击通过将代理/源DNN上的对抗扰动迁移到目标DNN来实现攻击。过往研究聚焦于对抗攻击的可迁移性，如Liu等人证明非针对性攻击比针对性攻击更易迁移；Wu等人和Demontis等人探索了影响可迁移性的因素，包括网络架构、模型容量和梯度对齐等。此外，还有多种提升对抗扰动可迁移性的方法，如动量迭代攻击（MI Attack）利用梯度动量提升可迁移性；方差减少攻击（VR Attack）通过平滑梯度生成高可迁移性的扰动；多样性输入攻击（DI Attack）对随机变换的输入图像进行对抗攻击；跳跃梯度方法（SGM Attack）利用跳跃连接的梯度提升可迁移性；平移不变攻击（TI Attack）用于规避经过鲁棒训练的DNN；Li等人利用随机失活侵蚀和跳跃连接侵蚀提升可迁移性。
2. 交互：输入变量间的交互研究广泛，Michel和Marc基于博弈论中的Shapley值提出Shapley交互指数；Daria Sorokina定义了加法模型中K个输入变量的交互；Scott Lundberg量化了树集成模型中输入变量对之间的交互。部分研究聚焦于用交互分析DNN，如Tsang等人基于DNN权重测量统计交互；Murdoch等人提出通过消除不同门的信息歧义来提取LSTM中的交互，Singh等人将该方法扩展到CNN；Jin等人量化单词的上下文独立性以分层解释LSTM；Janizek等人基于Hessian矩阵扩展了集成梯度方法来量化输入特征的成对交互，该方法要求DNN使用SoftPlus操作替代ReLU操作；Chen等人扩展归因方法，使用Shapley交互指数生成NLP任务的分层解释。相比之下，本文使用Shapley交互指数解释和改进对抗扰动的可迁移性。

---

可迁移性和相互作用之间的关系-The Relationship Between Transferability and Interactions

对抗攻击在博弈论中的理论理解-Theoretical Understanding Of The Adversarial Attack In Game Theory

该部分从博弈论角度深入剖析对抗攻击，为研究对抗样本迁移性与扰动交互关系提供理论依据，具体内容如下：

1. Shapley值在对抗攻击中的应用：在对抗攻击场景里，把扰动向量 $\delta$ 的各个维度视为参与博弈的“玩家”。利用Shapley值来衡量每个扰动单元 $i$ 对攻击效果的贡献。为此，需要定义扰动单元子集 $S$ 对于攻击的效用函数 $v(S)$，它表示在添加仅包含 $S$ 中扰动单元的扰动 ${\delta }^{(S)}$ 后，模型对样本分类结果偏离真实标签的程度，通过对比不同类别得分来衡量 ，即 $v(S)={\max }_{y^{\prime }\ne y}{h}_{y^{\prime }}(x+{\delta }^{(S)})-h_y(x+{\delta }^{(S)})$.
2. 扰动单元交互的定义与计算：引入Shapley交互指数来刻画扰动单元之间的交互作用。对于两个扰动单元 $i$ 和 $j$，其Shapley交互指数 $I_{ij}(\delta )$ 定义为 ϕ ( S i j ∣ Ω ′ ) − [ ϕ ( i ∣ Ω ∖ { j } ) + ϕ ( j ∣ Ω ∖ { i } ) ] \phi(S_{ij}|\Omega') - [\phi(i|\Omega\setminus\{j\})+\phi(j|\Omega\setminus\{i\})] ϕ(Sij​∣Ω′)−[ϕ(i∣Ω∖{j})+ϕ(j∣Ω∖{i})]。其中，$\varphi (S_{ij}|{\Omega }^{\prime })$ 是将 $i$ 和 $j$ 看作一个整体 $S_{ij}$ 时的Shapley值， ϕ ( i ∣ Ω ∖ { j } ) \phi(i|\Omega\setminus\{j\}) ϕ(i∣Ω∖{j}) 和 ϕ ( j ∣ Ω ∖ { i } ) \phi(j|\Omega\setminus\{i\}) ϕ(j∣Ω∖{i}) 分别是 $i$ 和 $j$ 单独作用时的Shapley值。该指数反映了在考虑其他扰动单元存在的情况下，$i$ 和 $j$ 共同作用对攻击效果的额外贡献。若 $I_{ij}(\delta )>0$，表明 ${\delta }_i$ 和 ${\delta }_j$ 相互协作，存在正交互；若 $I_{ij}(\delta )<0$，则表示两者相互冲突，存在负交互。
3. 多步攻击与单步攻击的交互差异分析：证明了多步攻击生成的对抗扰动中，扰动单元间的交互期望大于单步攻击。多步攻击通过梯度下降逐步更新扰动，最终扰动为 ${\delta }_{multi}^m=\alpha {\sum }_{t=0}^{m-1}{\nabla }_x\ell (h(x+{\delta }_{multi}^t),y)$；而单步攻击仅依据原始输入的梯度生成扰动，即 ${\delta }_{single}=\alpha m{\nabla }_x\ell (h(x),y)$。理论推导得出，多步攻击生成的扰动 ${\delta }_{multi}^m$ 中扰动单元间交互的期望 ${\mathbb{E}}_{a,b}[I_{ab}({\delta }_{multi}^m)]$ 大于单步攻击生成的扰动 ${\delta }_{single}$ 中扰动单元间交互的期望 ${\mathbb{E}}_{a,b}[I_{ab}({\delta }_{single})]$。这意味着多步攻击生成的扰动往往具有更强的扰动单元间协作关系，而这种强协作可能导致对抗扰动过度拟合源DNN，进而影响其在目标DNN上的迁移性 。

负相关关系的实验验证-Empirical Verification Of The Negative Correlation

该部分通过实验验证了对抗样本迁移性与扰动内部交互之间的负相关关系，具体内容如下：

1. 实验目的：验证对抗样本的可迁移性与对抗扰动内部交互之间是否存在负相关，即低可迁移性的对抗扰动是否比高可迁移性的扰动表现出更大的交互。
2. 实验设置
   • 衡量指标：用迁移效用（Transfer Utility）衡量对抗扰动的可迁移性，计算为 $[{\max }_{y^{\prime }\ne y}{h}_{y^{\prime }}^{(t)}(x+\delta )-h_y^{(t)}(x+\delta )]-[{\max }_{y^{\prime }\ne y}{h}_{y^{\prime }}^{(t)}(x)-h_y^{(t)}(x)]$；用 ${\mathbb{E}}_{i,j}[I_{ij}(\delta )]$ 衡量交互，为降低计算成本，通过证明将其简化为 1 n − 1 E i [ v ( Ω ) − v ( Ω ∖ { i } ) − v ( { i } ) + v ( ∅ ) ] \frac{1}{n - 1} \mathbb{E}_{i}[v(\Omega)-v(\Omega \setminus\{i\})-v(\{i\})+v(\emptyset)] n−11​Ei​[v(Ω)−v(Ω∖{i})−v({i})+v(∅)].
   • 实验数据与模型：从ImageNet数据集的验证集中随机抽取50张图像，在包括ResNet34/152和DenseNet - 121/201在内的四种DNN上生成对抗扰动，并将在每个ResNet上生成的扰动迁移到DenseNets，反之亦然。
   • 生成对抗扰动：通过求解 ${\min }_{\delta }-\ell (h(x+\delta ),y)+c\cdot \Vert \delta {\Vert }_p^p$ s.t. $x+\delta \in [0,1{]}^n$ 生成对抗扰动，通过改变超参数 $c$ 和 $p$ 的值来得到不同的对抗扰动。为保证不同超参数生成的扰动具有可比性，以 $\Vert \delta {\Vert }_2=\tau$ 作为所有对抗攻击的停止标准。
3. 实验结果：实验结果验证了负相关关系，如图1所示，每个子图对应特定的源DNN和目标DNN对，图中的点表示不同测试图像上对抗扰动的平均迁移效用和平均交互，不同点由不同超参数生成。结果表明，迁移效用与交互之间呈负相关，即对抗扰动的可迁移性越高，其内部交互往往越小。

图1：迁移效用与交互之间的负相关关系。相关性通过皮尔逊相关性计算得出。每个子图中的蓝色阴影表示线性回归的95%置信区间。

---

对可迁移性增强攻击的统一理解-Unified Understanding Of Transferability-Boosting Attacks

该部分从理论和实验两方面，证明经典提升对抗样本迁移性的方法本质是降低扰动单元间交互，为理解这些方法提供统一视角，具体内容如下：

1. VR Attack分析：VR Attack在攻击时用高斯噪声平滑分类损失，其梯度计算方式为 $g^t={\mathbb{E}}_{\xi \sim N(0,{\sigma }^{2}I)}[{\nabla }_x\ell (h(x+{\delta }^t+\xi ),y)]$。理论证明方面，通过对比VR Attack生成的扰动 ${\delta }_{vr}^m=\alpha {\sum }_{t=0}^{m-1}{\nabla }_x\hat{\ell }(h(x+{\delta }_{vr}^t),y)$（其中 $\hat{\ell }(h(x+{\delta }_{vr}^t),y)={\mathbb{E}}_{\xi \sim N(0,{\sigma }^{2}I)}[\ell (h(x+{\delta }_{vr}^t+\xi ),y)]$ ）和多步攻击生成的扰动 ${\delta }_{multi}^m=\alpha {\sum }_{t=0}^{m-1}{\nabla }_x\ell (h(x+{\delta }_{multi}^t),y)$，得出 ${\mathbb{E}}_x{\mathbb{E}}_{a,b}[I_{ab}({\delta }_{vr}^m)]\le {\mathbb{E}}_x{\mathbb{E}}_{a,b}[I_{ab}({\delta }_{multi}^m)]$，即VR Attack生成的扰动单元间交互更小。实验也表明，VR Attack的扰动单元间交互低于基线多步攻击，这验证了其降低交互的特性。
2. MI Attack分析：MI Attack在更新对抗扰动时结合了梯度动量，原始MI Attack与多步攻击因生成扰动幅度难以公平控制而无法直接比较，因此对MI Attack进行了轻微修改，修改后的梯度计算为 $g_{mi}^t=\mu g_{mi}^{t-1}+(1-\mu ){\nabla }_x\ell (h(x+{\delta }_{mi}^{t-1}),y)$（$\mu =(t-1)/t$） 。理论证明显示，修改后的MI Attack生成的扰动 ${\delta }_{mi}^m=\alpha {\sum }_{t=0}^{m-1}{g}_{mi}^t$，其扰动单元间的交互小于多步攻击生成的扰动，即 ${\mathbb{E}}_{a,b}[I_{ab}({\delta }_{mi}^m)]\le {\mathbb{E}}_{a,b}[I_{ab}({\delta }_{multi}^m)]$。这表明MI Attack在大多数情况下能减少扰动单元间的交互。
3. SGM Attack分析：SGM Attack利用ResNets中跳跃连接的梯度信息提升对抗扰动的迁移性，该方法在反向传播中修改梯度，类似在反向传播中添加特定的随机失活操作。由于已有研究证明随机失活操作可降低交互的显著性，从而减少DNN的过拟合，因此SGM Attack也降低了扰动单元间的交互。实验同样验证了SGM Attack的扰动单元间交互低于基线多步攻击，进一步支持了这一结论。

---

可迁移性增强的相互作用损失-The Interaction Loss For Transferability Enhancement

该部分主要介绍了为提升对抗样本迁移性而设计的交互损失方法，通过理论分析和大量实验验证其有效性，具体内容如下：

1. 交互损失的提出：基于前文发现的对抗样本迁移性与扰动内部交互的负相关关系，提出交互损失（interaction loss）来直接惩罚攻击过程中的交互，以提升对抗扰动的迁移性。在生成对抗扰动时，联合优化分类损失和交互损失，该方法称为交互减少攻击（IR Attack），其目标函数为 ${\max }_{\delta }[\ell (h(x+\delta ),y)-\lambda {\ell }_{interaction}]$，其中 ${\ell }_{interaction}={\mathbb{E}}_{i,j}[I_{ij}(\delta )]$ 是交互损失，$\lambda$ 是控制交互损失权重的常数。

2. 计算优化：由于高维图像中计算交互损失的成本过高，采取了两项优化措施。一是将输入图像划分为 $16\times 16$ 的网格，在网格级别而非像素级别测量和惩罚交互；二是运用高效采样方法近似计算交互损失中的期望操作，以此在保证一定准确性的同时降低计算成本。
   
   图2：有交互损失和无交互损失情况下生成的相邻扰动单元之间交互的可视化。可视化中的颜色是根据 $color[i]\propto E_{j\in N_i}[I_{ij}(\delta )]$ 计算得出的，其中 $N_i$ 表示扰动单元 $i$ 的相邻扰动单元集合。在这里，为简化可视化，我们忽略了非相邻单元之间的交互。这是因为相邻单元通常比其他单元编码更显著的交互。交互损失迫使扰动编码更多的负交互。

3. 实验验证

   • 实验设置：在包括Alexnet、VGG - 16等在内的六个不同源DNN上生成对抗扰动，并在多个目标DNN上测试其迁移性，同时使用了经过集成对抗训练的安全目标DNN进行测试。对比方法包括PGD Attack、MI Attack、VR Attack、SGM Attack、TI Attack等，还将交互损失应用于其他攻击方法（如MI + IR、VR + IR、SGM + IR）以及结合多种减少交互技术的HybridIR Attack。所有攻击实验均在ImageNet数据集的验证集上进行，设置了不同的参数，如 $ϵ$、步长、$\lambda$ 等，并采用留一法（LOO）验证来评估迁移性 。
   • 实验结果：IR Attack显著提升了对抗扰动的迁移性。在 $L_{\infty }$ 和 $L_2$ 攻击中，相比基线PGD Attack，IR Attack在不同源模型和目标模型上的迁移性提升明显，多数情况下提升幅度超过10%。在对集成模型的攻击实验以及针对安全目标DNN的攻击实验中，交互损失同样提升了迁移性。此外，将交互损失应用于其他攻击方法也进一步提升了其迁移性，HybridIR Attack的成功率提升尤为显著。
     表1：在包括AlexNet、VGG16、ResNet - 34/152、DenseNet - 121/201在内的六个源模型上生成的$L_{\infty }$和$L_2$黑盒攻击对七个目标模型的成功率。通过惩罚交互作用可以提高对抗扰动的可迁移性。
     
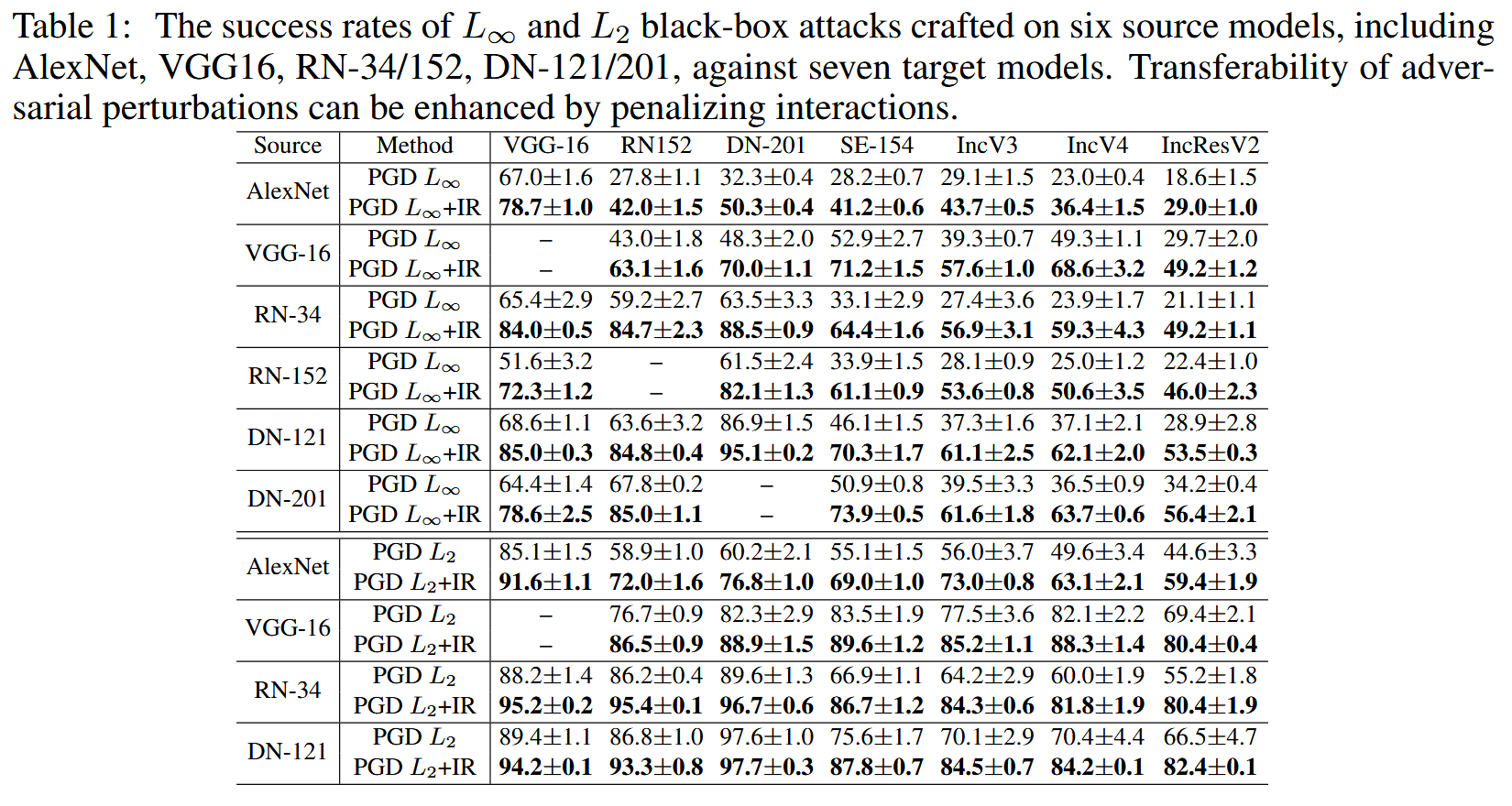
     表2：在集成模型（RN - 34+RN - 152+DN - 121）上生成的 $L_{\infty }$ 黑盒攻击对九个目标模型的成功率。
     
     表3：针对安全模型的迁移性：在RN-34和DN-121源模型上生成的 $L_{\infty }$ 黑盒攻击对三个安全模型的成功率。
     
     表4：不同方法在四个源模型（ResNet-34/152、DenseNet-121/201）上生成的 $L_{\infty }$ 黑盒攻击对七个目标模型的成功率。通过惩罚交互作用可以提高对抗扰动的可迁移性。
     

4. 交互损失的效果分析

   • 权重影响：测试了不同交互损失权重 $\lambda$ 对IR Attack迁移性的影响，发现随着 $\lambda$ 增加，IR Attack的迁移性提高。
   • 仅使用交互损失的情况：仅使用交互损失（不使用分类损失）生成的扰动仍具有一定的对抗迁移性。这表明此类扰动减少了DNN中的大部分交互，破坏了输入图像的推理模式，从而对模型产生对抗效果。
     
     图3：(a) 使用不同 $\lambda$ 值的IR攻击进行黑盒攻击的成功率。随着 $\lambda$ 值的增加，成功率也随之提高。(b) 仅使用交互损失（不使用分类损失）生成的对抗扰动的可迁移性。这类对抗扰动仍表现出一定程度的对抗可迁移性。位于最后一个epoch的点代表作为基线的噪声扰动的可迁移性。

---

结论-Conclusion

文章结论部分从多个角度对研究成果进行总结，涵盖理论证明、方法统一理解、新方法提出及新视角发现，具体内容如下：

1. 理论成果：从博弈论中交互的角度，深入分析了对抗扰动的可迁移性。证明了多步攻击相较于单步攻击，更易产生具有较大内部交互的对抗扰动。在此基础上，发现并部分证明了对抗扰动的可迁移性与内部交互之间存在负相关关系，即具有较高可迁移性的对抗扰动通常表现出更多的负交互。
2. 统一理解现有方法：证明了一些经典的提升对抗扰动可迁移性的方法，其本质是降低了扰动单元之间的交互。这一发现为理解现有提升可迁移性的方法提供了统一的视角，有助于深入认识这些方法的内在机制。
3. 新方法提出及效果：提出了一种新的损失函数——交互损失，该损失函数通过在攻击过程中直接惩罚扰动单元之间的交互，显著提升了先前方法中对抗扰动的可迁移性。在多个实验中，无论是针对不同的源模型和目标模型，还是在不同的攻击设置下，交互损失都展现出了良好的效果，有效提高了对抗攻击的成功率。
4. 新视角发现：发现仅使用交互损失而不使用分类损失生成的对抗扰动，仍然具有一定程度的可迁移性。这一现象为理解对抗扰动的可迁移性提供了新的视角，表明即使不依赖传统的分类损失，通过调整扰动的交互特性也能实现对抗攻击的效果，进一步拓展了对抗攻击研究的思路。