K-means聚类算法

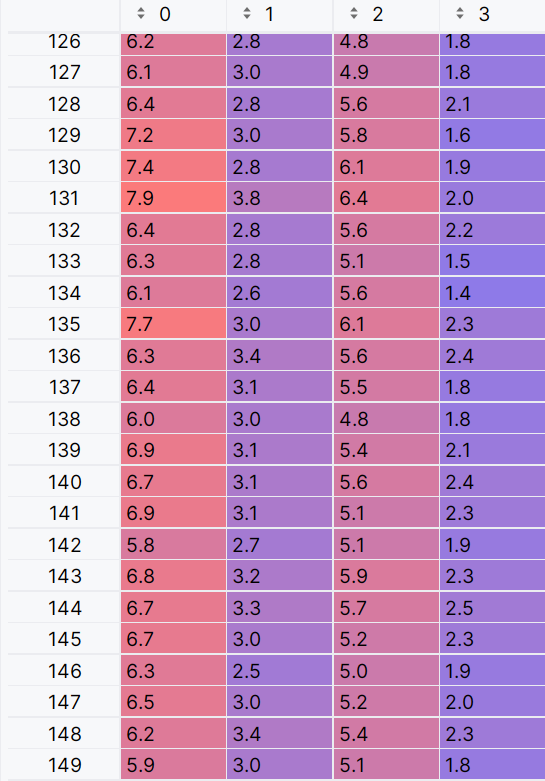
加载鸢尾花数据集，观察数据集特征。

鸢尾花数据集是一个经典的机器学习数据集，包含150个样本，每个样本有4个特征（花萼长度、花萼宽度、花瓣长度、花瓣宽度），共有3个目标类别（setosa、versicolor、virginica）。

实现K-Means算法, 运行并观察聚类结果

• 参数 K=3
• epochs(平均) =10

选取了两个指标（内部指标和外部指标）对聚类算法进行评估

1. 轮廓系数（Silhouette Coefficient）：轮廓系数度量聚类结果中每个样本的紧密度和分离度。它考虑了样本与其所属聚类的平均距离以及样本与最近邻聚类的平均距离。轮廓系数的取值范围在[-1, 1]之间，值越接近1表示聚类结果的紧密度和分离度较好。
2. 调整兰德指数（ARI）：ARI是一种用于评估聚类结果的外部指标，它衡量了聚类结果与真实标签之间的相似度。ARI的取值范围在[-1, 1]之间，值越接近1表示聚类结果与真实标签越相似，值越接近0表示两者之间的相似度接近于随机，而值越接近-1表示聚类结果与真实标签之间的相反关系。

实验结果

• 内部指标——轮廓系数: 0.5511916046195919
• 外部指标——调整兰德指数: 0.7163421126838476

本次实验的初始化中心的设置如下图所示

• 随机选取minJ和maxJ之间的数

初始聚类中心的设置 （K=3）

1. 不在minJ和maxJ之间的数

实验结果

• 内部指标——轮廓系数（只有一个类别，无法得出）
• 外部指标——调整兰德指数: 0（两者之间的相似度接近于随机）
• 此时只有一个类别（一个有效质点，两个无效质点）函数无法收敛，说明初始化中心点会影响聚类函数

2. 在minJ和maxJ之间的数，而且指定数字，尽量不会离得太远，对比随机选择，具有稳定性，但对应的不具有随机性

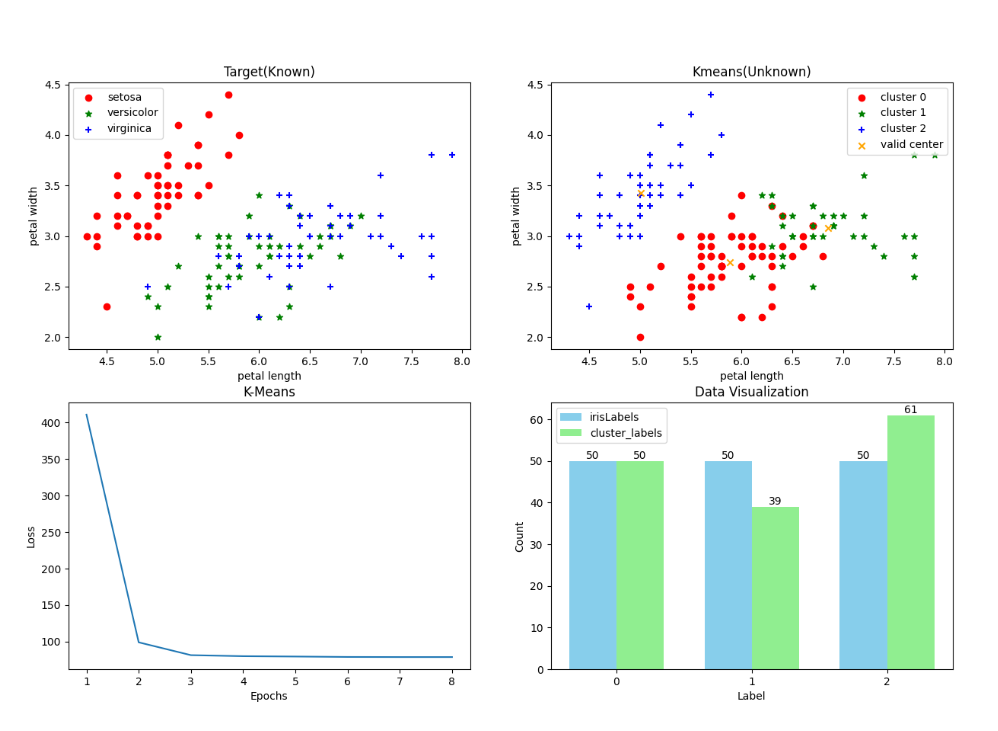
实验结果

• 内部指标——轮廓系数: 0.5511916046195919
• 外部指标——调整兰德指数: 0.7163421126838476
• epoch = 8

3. 在minJ和maxJ之间的数，而且指定数字，离得远一点

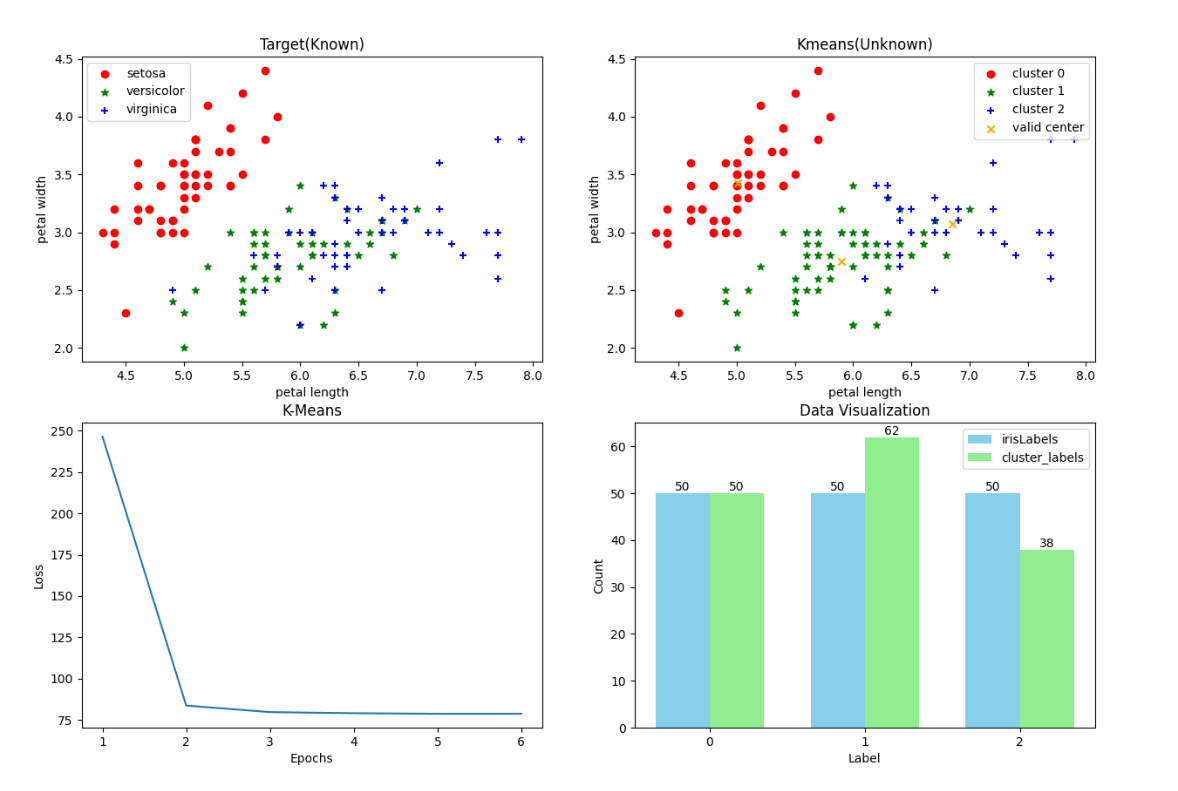
实验结果：

• 内部指标——轮廓系数: 0.5528190123564095
• 外部指标——调整兰德指数: 0.7302382722834697
• 此时收敛速度相对较快

4. Kmeans++算法

• 初始化第一个聚类中心：从数据集中随机选择一个样本作为第一个聚类中心。
• 计算每个样本与当前聚类中心之间的距离，并计算每个样本被选择为下一个聚类中心的概率。距离越远的样本被选中的概率越大，以确保聚类中心能够更好地分布在数据集中。
• 重复选择下一个聚类中心的过程，直到选择了k个聚类中心（k为预设的聚类数目）。在选择每个聚类中心时，使用加权概率的随机选择，以保证每个样本被选择为聚类中心的概率与其与最近的聚类中心的距离成正比。
• 使用选定的聚类中心进行标准的K-means迭代过程，包括样本分配到最近的聚类中心和更新聚类中心的步骤。
• 迭代步骤4，直到达到收敛条件（例如，聚类中心不再发生变化，或达到最大迭代次数）。

实验结果

• 内部指标——轮廓系数: 0.5528190123564095
• 外部指标——调整兰德指数: 0.7302382722834697
• 迭代次数相对较快

研究参数K对聚类结果的影响

不考虑无法收敛的情况
K = 4时

实验结果

• 内部指标——轮廓系数: 0.49764331793219224
• 外部指标——调整兰德指数: 0.5983278434991391
• 分成了4类

K = 5时

实验结果

• 内部指标——轮廓系数: 0.49308040671935205
• 外部指标——调整兰德指数: 0.6154838709677419
• 分成了5类

聚类算法的优缺点

K-means算法：

1. 优点：

• 简单、易于实现和理解。
• 可扩展性好，适用于大规模数据集。
• 对于球状簇具有较好的效果。

2. 缺点：

• 需要预先指定聚类数目k。
• 对于非球状簇或具有不同尺寸、密度的簇效果较差。
• 对初始聚类中心的选择敏感，可能陷入局部最优解。