离散234

原创已于 2022-11-11 12:28:17 修改 · 280 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法 #c语言

于 2022-11-05 16:19:18 首次发布

离散专栏收录该内容

2 篇文章

订阅专栏

本文介绍了一种基于布尔表达式的消解算法，通过不断解析和简化输入的布尔公式来判断其是否可满足。此外，还展示了矩阵的输入、运算及输出方法，并讨论了如何找出给定关系矩阵中的极小元与极大元。

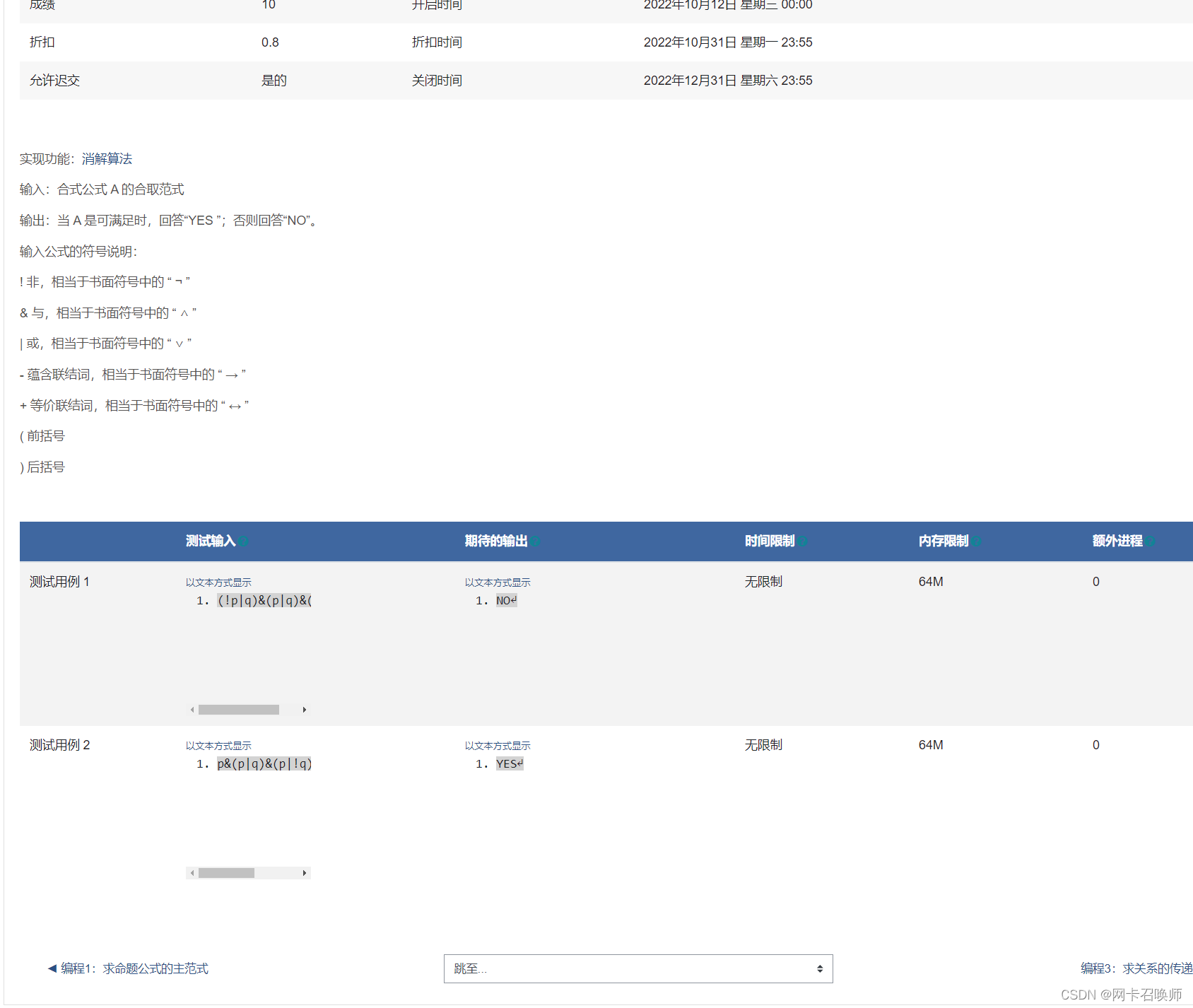
#include <bits/stdc++.h>  
using namespace std;//默认为主合取范式  
#define N 101  
int s[30][30];  
int s0,s1,s2;       //0-s0行 s0+1-s1 s2表示三个集合前两个代表跑1页s0，s1   
//书上说s2中没有任何元素结束shuchuyes ，指的是s1》=s2  
void baocun(char str[])  
{  
    int i,j,len=strlen(str);  
    for(i=0;i<30;i++)      
        for(j=0;j<30;j++)   
            s[i][j]=0;    
    s0=-1;  
    s1=-1;  
    s2=0;  
    for(i=0;i<len;i++)  
    {  
        if(str[i]<='z'&& str[i]>='a')  
        {  
            s[s2][str[i]-'a']=1;//是命题变元  
        }  
        else if(str[i]=='&')  
        {  
            s2++;  
        }  
        else if(str[i]=='!')  
        {  
            s[s2][str[++i]-'a']=2;//是否定的命题变元  
        }  
    }  
}  
int xiangtong(int s1[],int cc[])//判断两个析取式是否相等，? 这里有待争议不同则放入s2中  
{  
    for(register int i=0;i<26;i++)  
    {  
        if(s1[i]!=cc[i])  
        {  
            return 0;  
        }  
    }  
    return 1;  
}  
int judge(int c[]) //检查是否有重复 检查集合0，集合1，集合2中是否有重复  
{  
    int i;  
    for(i=0;i<=s2;i++)  
    {  
        if(xiangtong(s[i],c))  
        {  
            return 0;  
        }  
          
    }return 1;  
}  
int res(int a[],int b[])  
{  
    int yes=0;//成对可消解  
    int no=0;//不能消解  
    int c[30];           //中间用来存储res（c1,c2) 指的是s1中的每一对字句,s的每一行存储一个简单析取式 0-25 一开始赋值为0，代表a-z，有就赋值为1  
    for(register int i=0;i<26;i++)  
    {  
        if(!a[i]&&!b[i])   
            continue;  
        if((a[i]==1&&b[i]==2)||(a[i]==2&&b[i]==1))  
        {  
            yes++;  
        }  
        else  
            no++;  
    }  
  
        if(yes!=1) //没有可以消解或者多对可以消解  
        {  
            return 1;  
        }  
        if(!no) //全都可以消解  
        {  
            return 0;  
        }  
        for(register int i=0;i<26;i++) //计算res（c1,c2)  
        {  
            if((a[i]+b[i]==3)||(!a[i]&&!b[i])) //消没了或者本来就没有  
            {  
                c[i]=0;  
            }  
            else if(a[i]==1||b[i]==1) //两个析取式至少一个有该项变元  
            {  
                c[i]=1;  
            }  
            else   
            {  
                c[i]=2;  
            }  
        }  
        if(judge(c))//判断新得到的析取式是否已经存在  
        {  
            s2++;//s2-s1临时集合范围+1  
            for(int i=0;i<26;i++)  
            {  
                s[s2][i]=c[i];  
            }  
        }    
        return 1;   
}  
int main()  
{  
    char str[N];  
    scanf("%s",str);  
    baocun(str);  
    int i,j;  
    do  
    {  
        s0=s1;  
        s1=s2;  
        for( i=0;i<=s0;i++)//至少经过一次消解的情况  
        {  
            for( j=s0+1;j<=s1;j++)  
            {  
                if(!res(s[i],s[j]))  
                {  
                    cout<<"NO"<<endl;  
                    return 0;  
                }  
            }  
        }  
        for( i=s0+1;i<=s1;i++)//第一次进行消解的情况,s1内部进行消解  
        {  
            for( j=i+1;j<=s1;j++)  
            {  
                if(!res(s[i],s[j]))  
                {  
                    cout<<"NO"<<endl;  
                    return 0;  
                }  
            }  
        }  
    }while(s2>s1);//将新加的简单析取式仍然利用s2计数，若无新出现的简单析取式，s2集合为0，则跳出循环  
    cout<<"YES"<<endl;  
}  
//分为s0,s1,s2三个集合，每次循环之后将新出现的简单析取式加入s2中，之后将s2赋值给s1，将上一次的s1赋值给s0，再次进行消解，若中间过程出现完全消解，即得到0，直接得结果，不能得到可满足式，若之后的循环中s2中再无新元素加入，则可得到可满足式

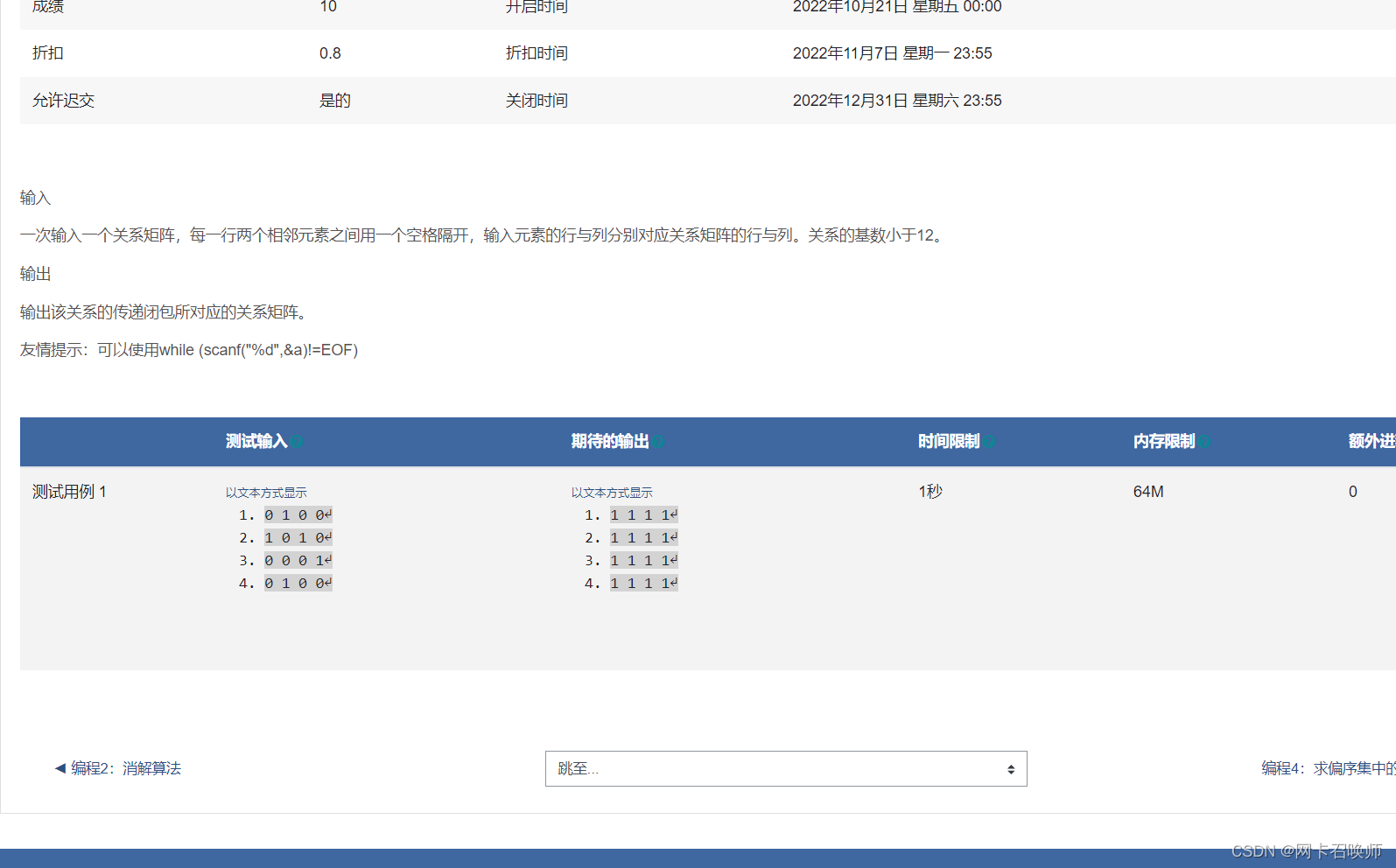
#include <bits/stdc++.h>  
using namespace std;  
int N;  
int a[25][25];  
void juzhen()//因为不知道N行列，所以先统一输在一行  
{  
    int tong[100];  
    int n=0;  
    int num;  
    while(scanf("%d",&num)==1)  
    {  
        tong[n++]=num;  
    }  
    N=(int)sqrt(n);  
    n=0;  
    for(int i=0;i<N;i++)  
    {  
        for(int j=0;j<N;j++)  
        {  
            a[i][j]=tong[n++];  
        }  
    }  
}  
void output()  
{  
    for(int i=0;i<N;i++)  
    {  
        for(int j=0;j<N;j++)  
        {  
            cout<<a[i][j];  
            if(j<N-1) cout<<" ";  
        }  
        cout<<endl;  
    }  
}  
void warshall()  
{  
    for(int k=0;k<N;k++)  
    {  
        for(int i=0;i<N;i++)  
        {  
            for(int j=0;j<N;j++)  
            {  
                a[i][j]=a[i][j]|a[i][k]*a[k][j];  
            }  
        }  
    }  
}  
int main()  
{  
    juzhen();  
    warshall();  
    output();  
    return 0;  
}

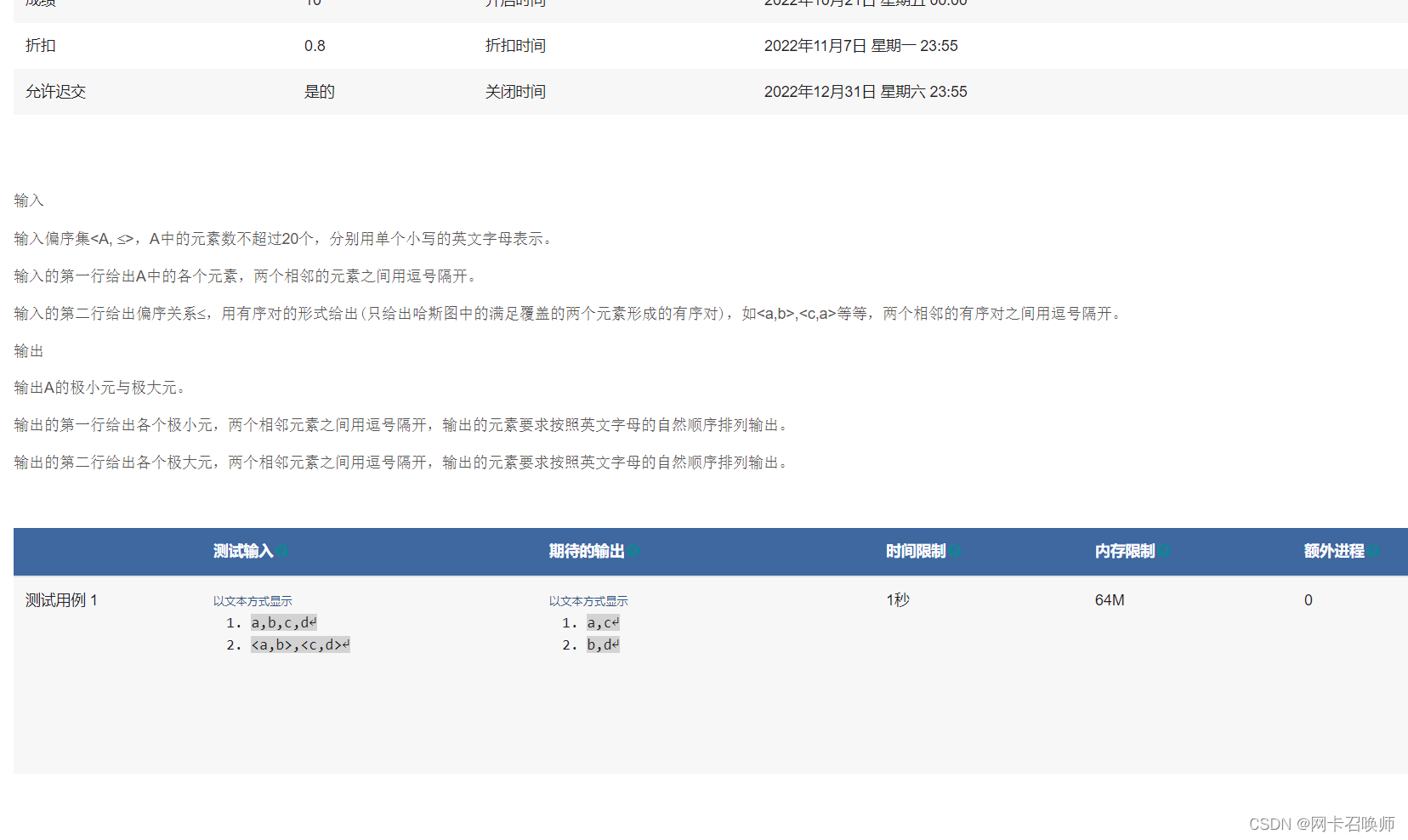
#include <bits/stdc++.h>  
using namespace std;  
#define N 50  
int d[N],min1[N],max1[N];  
void xiao()//shuchu极小元  
{  
    int i=0;  
    while(!d[i]||!min1[i]) i++;  
    printf("%c",i+'a');  
    for(int j=i+1;j<26;j++)  
    {  
        if(d[j]&&min1[j])   
            printf(",%c", j + 'a');  
    }  
    cout<<endl;  
}  
void da()  
{  
    int k=0;  
    while(!d[k]||!max1[k]) k++;  
    printf("%c",k+'a');  
    for(int j=k+1;j<26;j++)  
    {  
        if(d[j]&&max1[j])  
            printf(",%c",j+'a');  
    }  
    cout<<endl;  
}  
int main()  
{  
    memset(d,0,sizeof(d));//元素是否存在  
    memset(min1,1,sizeof(min1));  
    memset(max1,1,sizeof(max1));  
    char c;  
    while((c=getchar())!='\n')  
    {  
        if(c>='a'&& c<='z')  
            d[c-'a']=1;//标记有该元素  
    }  
    c=getchar();//换行符  
    while(c!='\n')  
    {  
        while(c<'a'||c>'z') c=getchar();//吸收掉<和，  
        max1[c-'a']=0;  
        c=getchar();//吸收掉，  
        while(c<'a'||c>'z')//吸收掉，  
        c=getchar();//一直到找到一个元素，因为在《=号后面，因此不是极小值  
        min1[c-'a']=0;  
        c=getchar();  
        while(c!='\n'&&(c<'a'||c>'z'))  
        c=getchar();  
    }  
    xiao();  
    da();  
}