FOC中的Clark变换一步步推导+Simulink仿真+仿真工程

本人水平有限，难免会有纰漏，如果发现哪里不对，望大家指出

1：理论推导

1-1：目的：将复杂的三相系统（在abc坐标系中）解耦成可以独立控制的两相系统，从而降低控制的复杂度。

1-2：推导过程：利用三角函数来实现三相坐标系(abc)到两相正交坐标系(αβ)

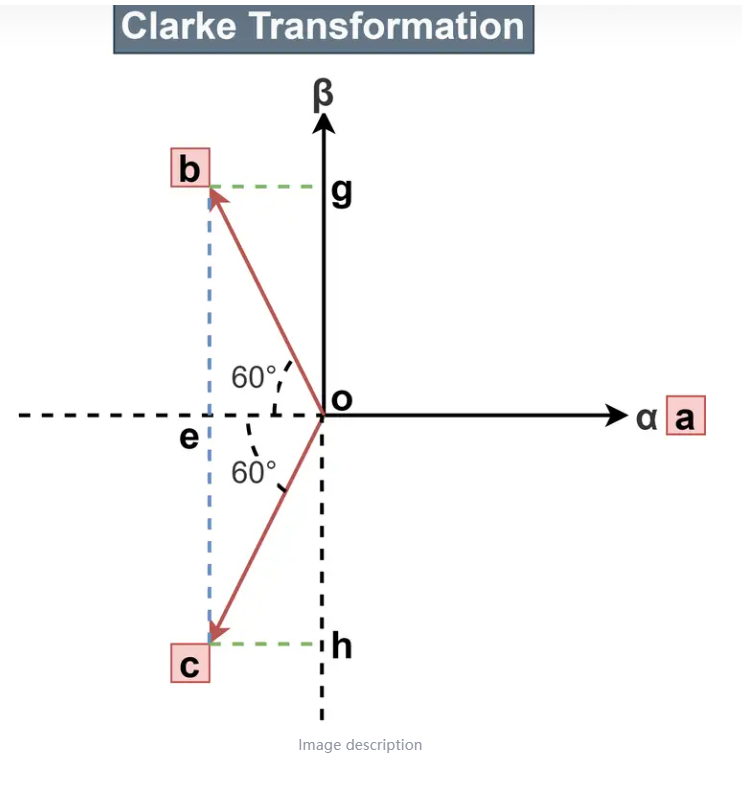
网上大多是用矩阵推导的，对新手可能不太好理解，下面我将用正交分解的方法推导

已知三相系统中的三相电流（Ia Ib Ic是幅值一样，频率一样，相位互差120度），且根据基尔霍夫电流定律，流入流出节点的电流代数和为0，Ia + Ib + Ic = 0

对于α轴，规定α为正方向，la与α轴重合，Ib,Ic与α轴负方向的夹角为60°，投影到上面的分量就是 Ib * cos60° 和 Ic * cos60°。所以Iα = Ia - cos60° * （Ic + Ib）。

对于β轴，以为Ia与β轴垂直（cos90°），所以在β轴不存在Ia的分量。只有Ib * cos30° 和** Ic * cos30°**，那个Iβ = cos30° * (Ib - Ic)

经过上面的操作 *Iα = Ia - 1/2 * (Ic + Ib) Iβ = sqrt(3) / 2 (Ib - Ic)

又因为 Ia + Ib + Ic = 0 所以将Ic = -(Ia + Ib带入得到)

Iα = 3 / 2 * Ia Iβ = sqrt(3) /2 * (Ia + 2 * Ib)

因为是基于等幅值的变换 所以 Iα 和 Iβ 要乘以一个系数 2/3。这个系数会在SVPWM中乘回来，不会对控制有什么影响，乘以这个系数是为了确保变换前后信号的幅值不变。
乘2/3后 ：Iα = Ia Iβ = sqrt(3) /3 * (Ia + 2Ib)
以上就是Clark变换的理论部分，接下来simulink仿真！！！！

2：Simulink模型搭建

2-1：添加信号源

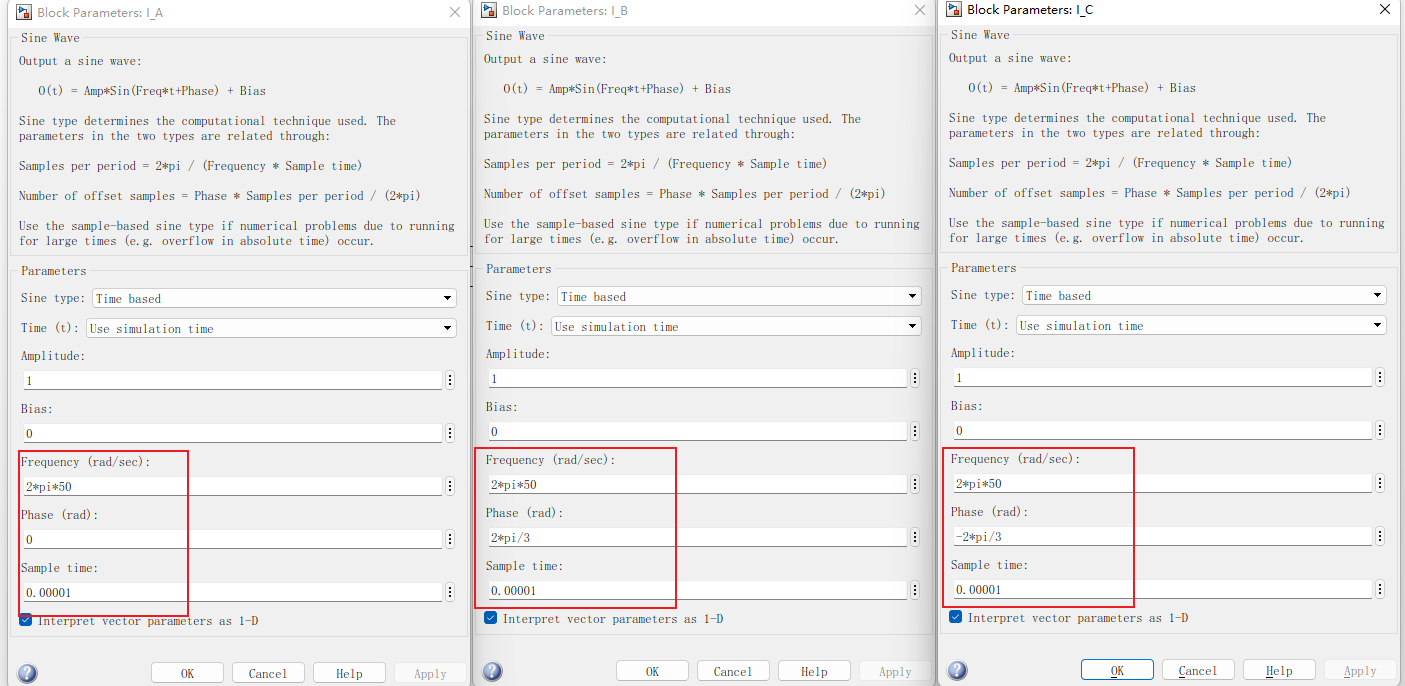
在simulink添加 Sine wave 具体信号源设置如下 ，要保持幅值（1A），频率一致（50HZ），且相位互差120°

添加个Scope模块查看产生的三相电流

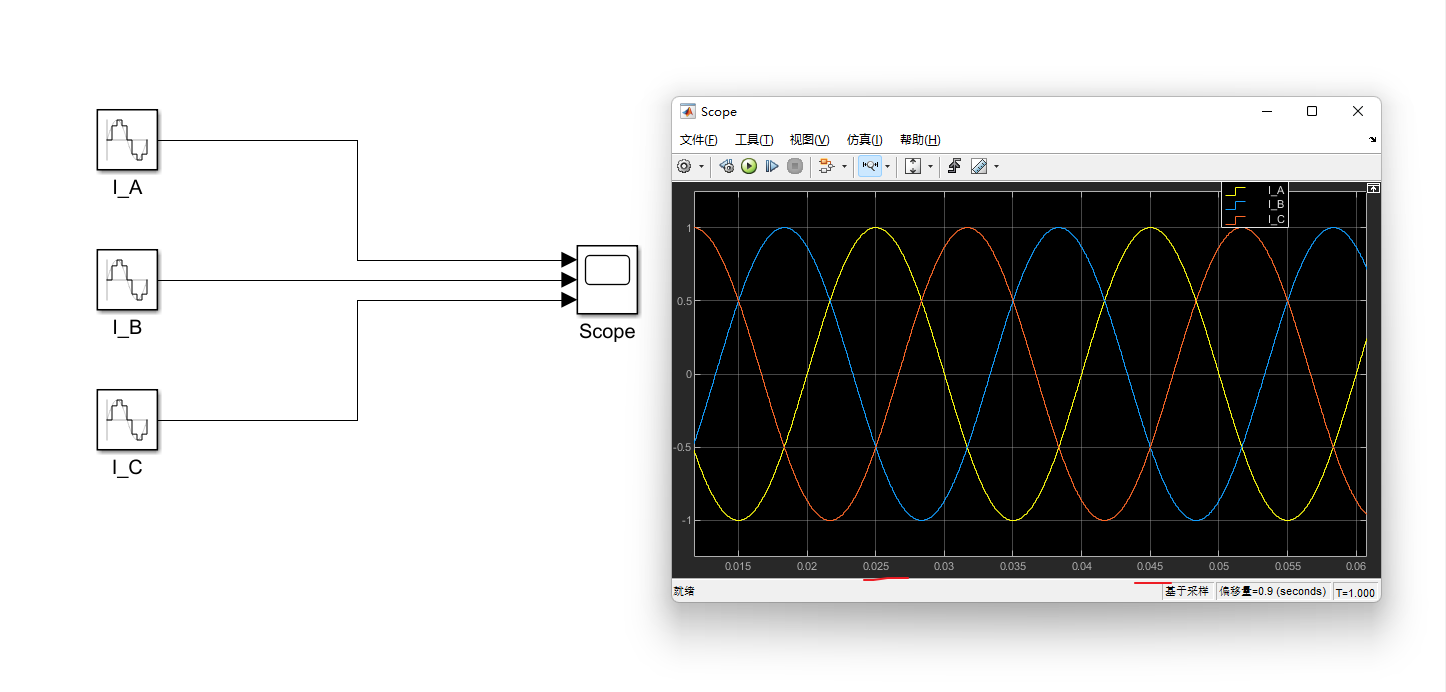
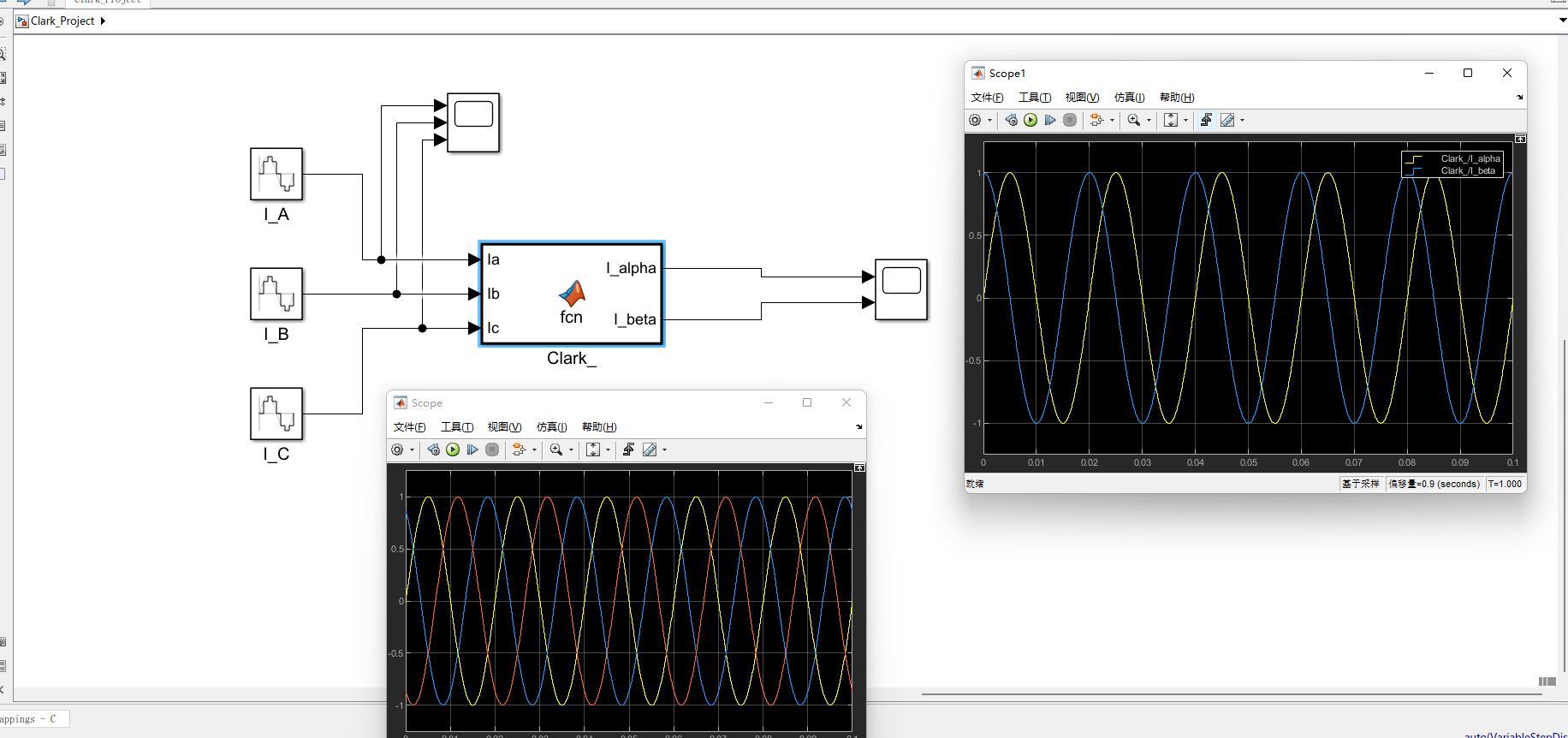
发出来的三相波形如上，验证了 幅值（1A），频率一致（50HZ），且相位互差120°的三相电流。

2-2：公式编写 + 验证

在simulink添加 MATLAB Function1 模块 双击 MATLAB Function1进入编辑器

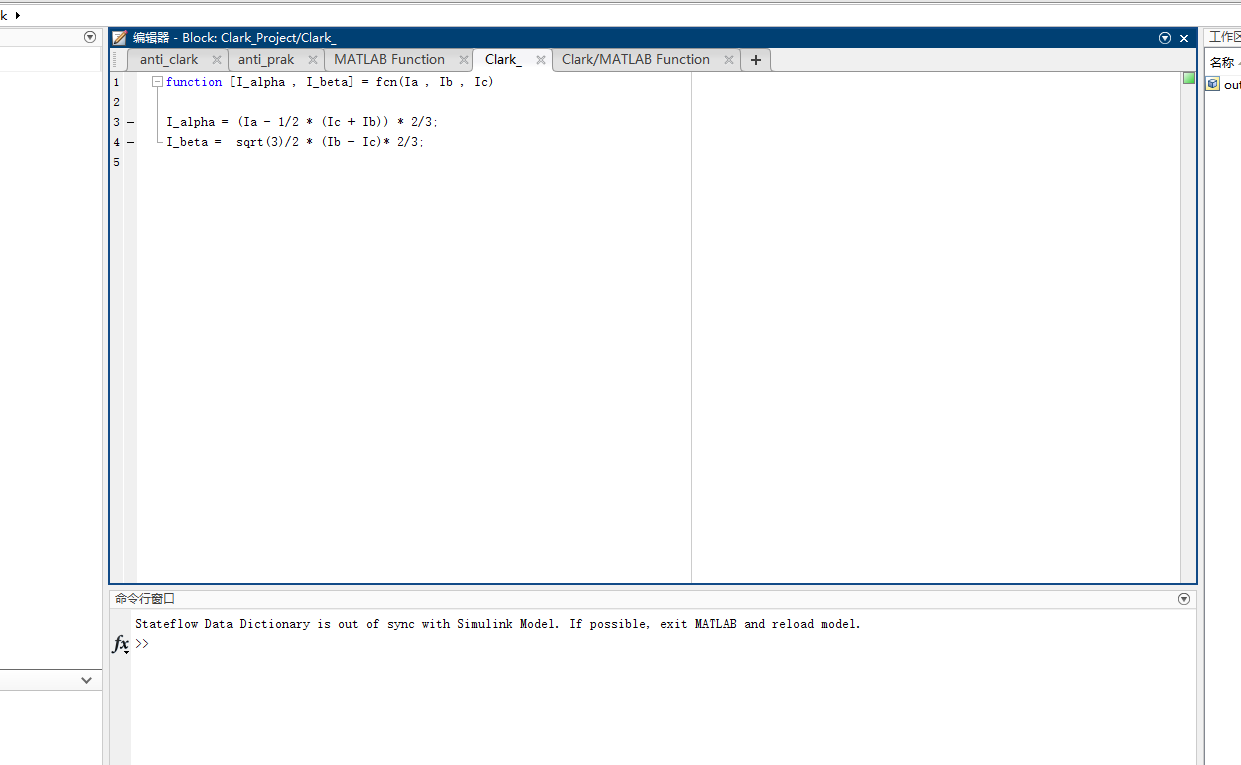
function [I_alpha , I_beta] = fcn(Ia , Ib , Ic)
I_alpha = (Ia - 1/2 * (Ic + Ib)) * 2/3;
I_beta =  sqrt(3)/2 * (Ib - Ic)* 2/3;

仿真后的波形就从最开始的三相变为两相，变换后的波形幅值和频率不变，相位互差90°。

如果把2/3这个系数去掉：

function [I_alpha , I_beta] = fcn(Ia , Ib , Ic)
I_alpha = (Ia - 1/2 * (Ic + Ib));
I_beta =  sqrt(3)/2 * (Ib - Ic);

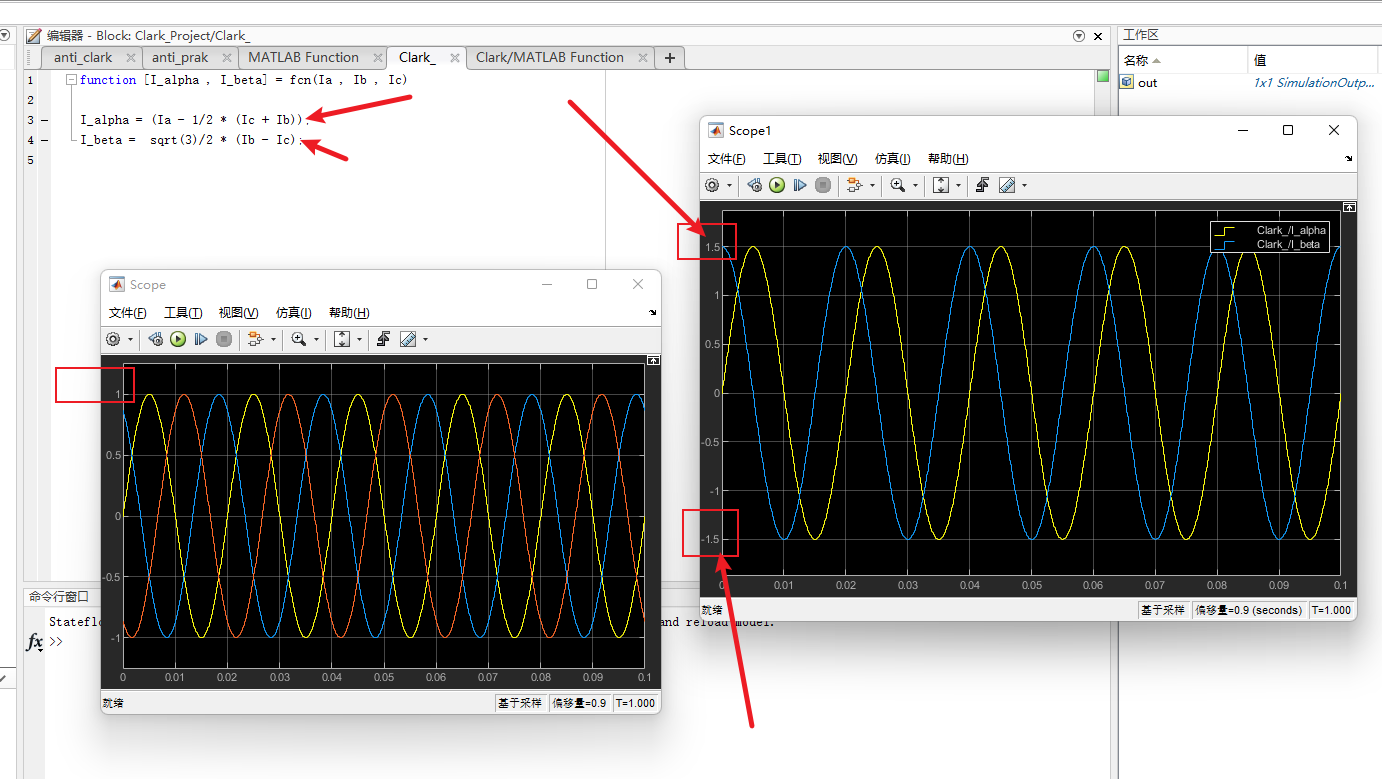
去掉系数后，经过Clark变换后的波形幅值就会变为原来的1.5倍，变换前后幅值发送了变化，就不是等幅值变化了。

这里clark变换的公式用了Ia Ib Ic三个变量

function [I_alpha , I_beta] = fcn(Ia , Ib , Ic)
I_alpha = (Ia - 1/2 * (Ic + Ib)) * 2/3;
I_beta =  sqrt(3)/2 * (Ib - Ic)* 2/3;

当然也可以采用上面推导的，都是一样的，就是把Ic = -(Ia + Ib)带入做抵消了

function [I_alpha , I_beta] = fcn(Ia , Ib)
I_alpha =  Ia;
I_beta = sqrt(3) /3  * (Ia + 2*Ib);

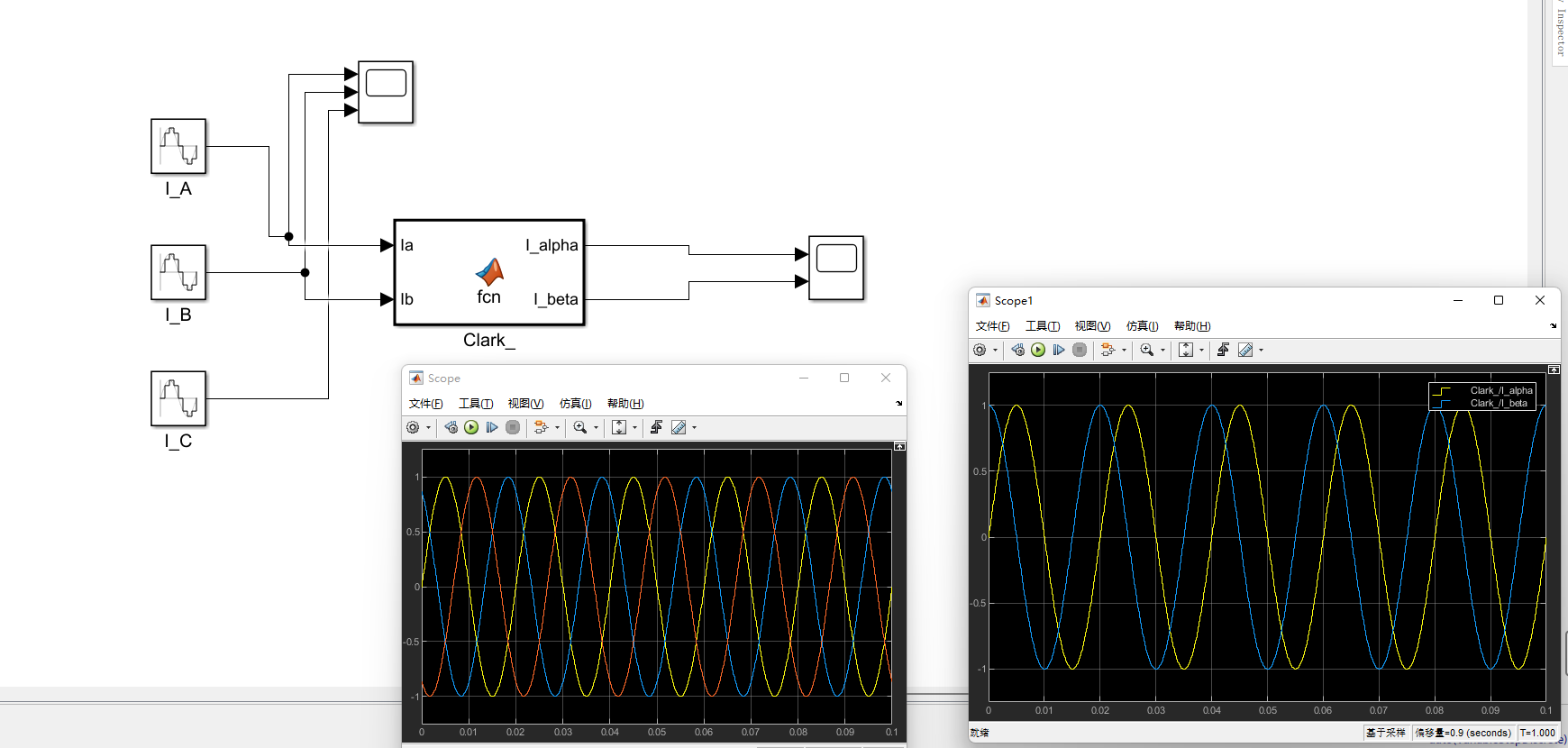
至此，已经将Clark变换的推导和仿真验证完。

3：simulink工程
通过百度网盘分享的文件：clark.zip
链接：https://pan.baidu.com/s/1T0UJqrr9zMmU0iNpyyPRLA
提取码：lina