时间序列预测——一文搞懂什么是时间序列

最新推荐文章于 2025-02-06 22:53:32 发布

G.E.N.

最新推荐文章于 2025-02-06 22:53:32 发布

阅读量3k

点赞数 27

文章标签：人工智能算法机器学习

本文链接：https://blog.csdn.net/qq_63708623/article/details/144872224

版权

一、为什么要做序列预测

万物皆序列。序列预测是基于历史数据推测未来趋势或状态的过程，广泛应用于各个行业。无论是股票市场、天气预测、生产调度还是流量预测，序列预测为我们提供了对未来的洞察力，帮助做出更加科学的决策。

序列数据本质上包含了随时间变化的模式、趋势和周期性。通过对这些历史数据的分析，我们可以识别出潜在的规律，并使用这些规律来预测未来。序列预测不仅是为了单纯的预测未来，而是为了提供数据支持的决策依据。无论是在商业决策、生产计划还是资源分配方面，预测的结果都可以帮助我们做出更好的决策。

二、什么是时间序列

时间序列（Time Series）是指按照时间顺序排列的一系列数据点，每个数据点通常在特定时间戳上被收集和记录。简而言之，时间序列是一种按时间维度组织的数据，它能够反映一个变量在不同时间段的变化趋势或行为模式。

时间序列数据的核心特征在于时间依赖性，即数据点之间通常存在某种内在的时间序列关系，当前时刻的数据往往受到之前时刻数据的影响。这种依赖关系是时间序列分析和预测的关键所在。

时间序列的特点如下：

顺序性：时间序列数据具有时间顺序特征，时间是数据的一个重要维度，数据点不是独立的，它们的顺序性对分析至关重要。每个数据点与时间戳相关联，且往往根据时间流逝而有一定的顺序。
时间依赖性：时间序列中的数据点通常是相互依赖的，即某一时刻的数据通常与之前或之后的时间点有着统计上的关系，这种依赖关系决定了如何预测未来的数据。
周期性：许多时间序列数据展示出周期性变化，例如每年夏季的温度变化、股票市场的季节性波动等。
趋势性：趋势是指时间序列数据在较长时间段内表现出的上升或下降趋势。例如，股票市场价格的长期上涨趋势、经济数据的增长趋势等。
季节性和噪声：季节性波动通常是由季节、节假日等因素引起的规律性变化，而噪声则是指数据中的随机波动部分，通常不携带有意义的信息。

为了能够更加清晰的讲述时间序列数据，我们使用ETDataset作为示例。ETDataset下载地址如下：

GitHub：GitHub - zhouhaoyi/ETDataset：收集 Electricity Transformer 数据集是为了支持对长序列预测问题的进一步研究。https://github.com/zhouhaoyi/ETDataset也可以在我的百度网盘下载：
链接: https://pan.baidu.com/s/1rvWZoJcFau3a-bHCdZJP-A?pwd=ekcg 提取码: ekcg

数据集介绍

电力分配问题是将电力分配到不同地区的问题，这取决于电力的使用顺序。但是，预测特定区域的后续需求非常困难，因为它随工作日、节假日、季节、天气、气温等因素而变化。因此，目前由于没有一种有效的方法来预测未来的用电量，管理人员只能根据经验数字做出决策，而这个数字远远高于现实世界的需求。这会造成不必要的电力浪费和设备折旧。另一方面，油温可以反映电力变压器的状况。最有效的策略之一就是预测电力变压器的油温是否安全，避免不必要的浪费。因此，为了解决这一问题，ETDataset团队与北京国网富达科技发展有限公司共同建立了一个真实世界平台，并收集了两年的数据。利用它来预测变压器的油温，并研究极端负荷能力。
ETDataset提供了两年的数据，其中每个数据点每分钟记录一次（以 m 标记），它们来自中国某省的两个地区，分别命名为 ETT-small-m1 和 ETT-small-m2。每个数据集包含 2 年 * 365 天 * 24 小时 * 4 次 = 70,080 个数据点。此外，ETDataset还提供了用于快速开发的小时级变体（以 h 标记），即 ETT-small-h1 和 ETT-small-h2。每个数据点由 8 个特征组成，包括点的日期、预测值 “油温 ”和 6 种不同类型的外部功率负荷特征。

我们选择数据量较小的ETTh1.csv文件作为案例。ETTh1同样是两年的数据，只不过每小时采样一次，共有17420个数据点。

打开ETTh1.csv，数据内容如下：

数据一共有8列，含义分别如下：

date	记录数据的时间
HUFL	高有效负载
HULL	高无效负载
MUFL	中有效负载
MULL	中无效负载
LUFL	低有效负载
LULL	低无效负载
OT	电力变压器的油温（需要预测的值）

我们将除时间外的7个列，称为7个特征。其中6个负载特征是电力系统中的专用语，我们不需要知道具体的含义。OT则是我们需要预测的油温。

数据分析

数据分析是探索数据内部规律的最常用的手段。

我们可以在Jupyter Notebook中，对ETTh1.csv进行分析，代码如下：

import pandas as pd

df = pd.read_csv('ETTh1.csv')
df.head()

我们可以看到文件前五行的数据：

跟前面的截图一致，证明数据读取成功。

接下来我们可以使用describe函数，对数据的统计值进行分析。

df.describe()

可以看到，7个特征的统计量都被展示了出来，其中8个统计量含义如下：

count	有效值个数
mean	平均值
std	标准差
min	最小值
25%	25%分位数
50%	中位数
75%	75%分位数
max	最大值

我们也可以从中发现以西数据的规律，例如OT（油温）的标准差最大，说明油温的波动程度最大；LULL的标准差最小，说明LULL的波动程度最小。

为了更加直观的观察数据的变化，我们可以取前200条数据，并绘制出来。

import matplotlib.pyplot as plt

# 取前200条数据
data_show = df.iloc[:200, :]

# 取所有特征列
features = data_show.iloc[:, 1:]

# 创建3x3的子图
fig, axes = plt.subplots(3, 3, figsize=(15, 10))

# 将axes数组展平成一维数组，方便进行迭代
axes = axes.flatten()

# 绘制每个特征的变化
for i, col in enumerate(features.columns):
    axes[i].plot(features[col])
    axes[i].set_title(f'Feature {col}')
    axes[i].set_xlabel('Time')
    axes[i].set_ylabel(f'{col}')

# 如果子图数量少于9个，可以将多余的子图隐藏
for j in range(i+1, 9):
    axes[j].axis('off')  # 隐藏多余的子图

# 调整布局
plt.tight_layout()
plt.show()

得到结果如下：

此外，还可以将所有特征绘制在一张图上，以对比不同数据的差异。

plt.show()
#%%
for col in features.columns:
    # 将所有数据绘制在一张图
    plt.plot(features[col], label=col)

# 显示图例
plt.legend()
plt.xlabel('Time')
plt.ylabel('Value')

plt.show()

结果如下：

我们可以发现，6个负载特征的变化趋势比较相似，而油温与负载之间的关系难以肉眼观察。

我们可以通过计算相关性矩阵，得到7个特征之间的相关性。

import seaborn as sns

# 获取所有数据的特征
features = df.iloc[:, 1:]
# 计算相关性矩阵
correlation_matrix = features.corr()
# 使用热图可视化相关性矩阵
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', linewidths=0.5, fmt='.2f', vmin=-1, vmax=1)
plt.title('Correlation Matrix Heatmap')
plt.show()

相关性分析是用来评估不同特征之间的相关程度。对于数值型数据，可以使用皮尔逊相关系数（Pearson Correlation Coefficient）来量化两个变量之间的线性相关性。相关系数的值范围从 -1 到 1，分别表示完全负相关、无相关性和完全正相关。X与Y两个随机变量的皮尔逊相关系数计算如下：

$\rho _{X,Y}=\frac{Cov(X,Y))}{\sigma X\sigma Y}$

我们可以将数据中的每一个列视作为一个随机变量。

相关性矩阵是每个特征两两之间形成的皮尔逊相关系数矩阵，是一个对称矩阵，矩阵如下：

我们可以从相关性矩阵中得到以下几点信息：

HUFL与MUFL高度相关，相关性高达0.99
HULL与MULL高度相关，相关性高达0.93
HULL与MULL与预测值OT具有微弱的相关性，相关性为0.22

对于高相关性的特征，为了节省计算资源，我们可以考虑将其中一个特征删除，因为高度相关的特征表达的信息一致，容易造成信息的冗余。但也可以不采取措施，毕竟相关性不是完全为1。

时间序列

在了解了数据特性之后，我们接下来要将数据处理成序列。

我们前面介绍的数据是一个表格，还无法称之为时间序列。时间序列是由多个时间点组成的、在一定时间范围内的序列，简单来说，时间序列是表格的一个连续的部分。

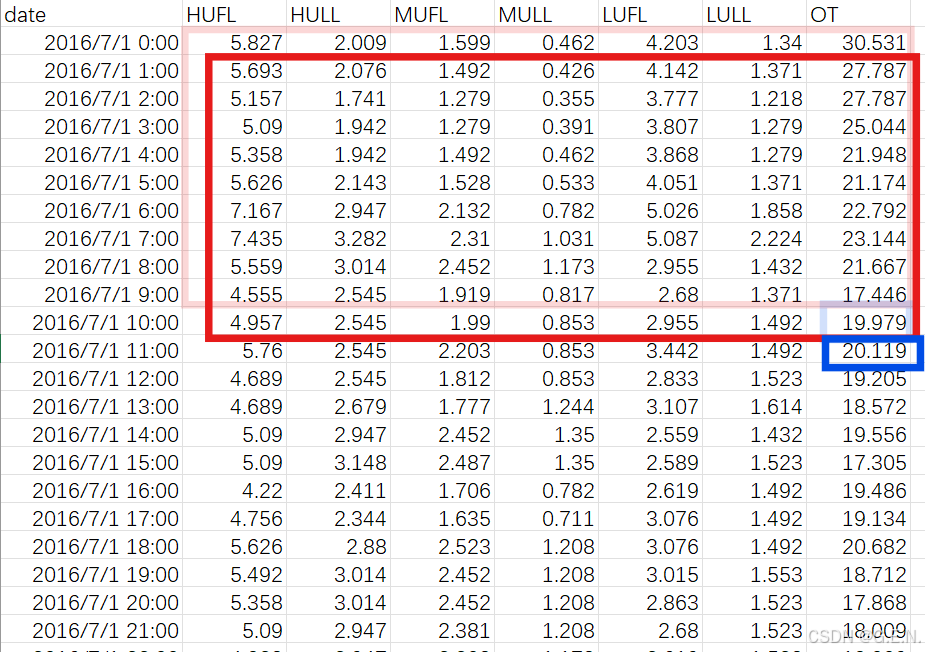
在上面的图中，我用红色的框框选了2016/7/1 0:00至 2016/7/1 9:00这10行数据，这10行数据是10个连续的时间点，因此我们将这10行数据，称作为长度为10的时间序列。

我们最终要做的任务就是，根据用红色框框选的数据，预测出蓝色框框选的值。

换句话说，红色数据是过去10小时数据的数据，蓝色框是未来1小时的值。要用过去10小时的数据预测未来1小时的油温。

时间序列的视任务不同要求而定，有时希望用过去60个时间点，预测出未来1个时间点，那么此时时间序列的长度为60。

一个表格数据可以切分出多个时间序列。例如，在切分完第一个时间序列后，我们可以将窗口向下移动一个时间点，此时就可以来切割第二条时间时间序列。

时间序列分割代码如下：

# 所有时间序列
sequences = []
# 所有时间序列的标签
labels = []

# 时间序列长度
seq_length = 10
features = df.iloc[:, 1:].values

# 计算可以切割出多少个序列
num_sequences = len(features) - seq_length

# 按照时间序列长度切分数据
for i in range(num_sequences):
    # 截取时间序列
    sequence = features[i: i + seq_length, :]  # 获取从i到i+seq_length的数据
    # 获取标签
    label = features[i + seq_length, -1]
    
    # 保存序列与标签
    sequences.append(sequence)
    labels.append(label)

for seq, label in zip(sequences, labels):
    print(seq.shape, label)

在完成时间序列的切分后，打印时间序列的形状与标签值，其中部分输出如下：

(10, 7) 19.97900009155273
(10, 7) 20.11899948120117
(10, 7) 19.20499992370605
(10, 7) 18.57200050354004

（10，7）为时间序列的形状，10表示时间序列的长度（10个时间点），7表示特征的数量（7个特征），后面的数字表示未来一小时的油温。

因此，时间序列预测任务，实际上就是寻找一个从时间序列矩阵到预测值的映射，使得输入时间序列（形状为10，7的矩阵），输出一个值，并使得输出值与标签值尽可能的相似。