微分方程的建立
目的:为建立LTI系统的数学模型,需要列写微分方程式。
以RLC电路为例:
以Us为输入,Uc为输入,则可以得出以下微分方程式:
抽去物理意义后,得到一般的常微分线性方程:
相似系统
指性质不同的两个物理系统,它们的数学模型却能一一对应(或者说由这两个系统得出的微分方程形式完全相同),则称这两个系统互为相似系统。
用微分方程不仅可以建立描述电路、机械等工程系统的数学模型,而且还可以用于构建生物系统、经济系统、社会系统等各种科学领域。
模拟框图表示
模拟框图:指将抽象的微分方程用基本部件的相互连接所表达出的直观的图。简称:框图。
基本公式:
或者写为:
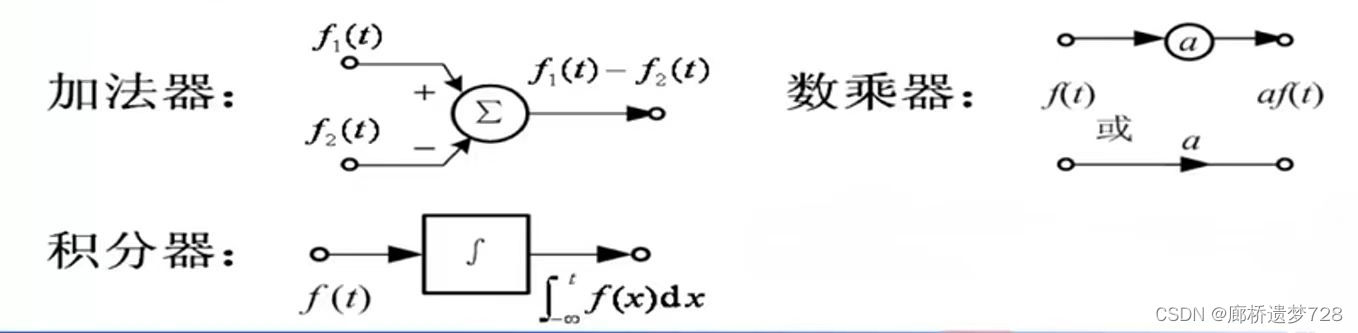
基本运算:数乘、微分、积分、相加
基本部件:加法器、数乘器、积分器(通常不用微分器,抗干扰性差、不稳定)
微分方程转化为框图
中间变量法
设激励f(t)产生x(t),x(t)产生响应y(t)。
设f(t)=关于x(t)的一个函数式,其函数式与原式中y(t)函数式相同;y(t)=关于x(t)的另一个函数式,其函数式与原式中f(t)函数式相同。
证明:
将原微分方程记作
的形式
令f(t)线性变换为
,由LTI系统的线性规则可得:
又
,可得:
例题:

对于其输入带微分的常微分方程常使用此方法求框图。当输入无微分时,可直接求框图。
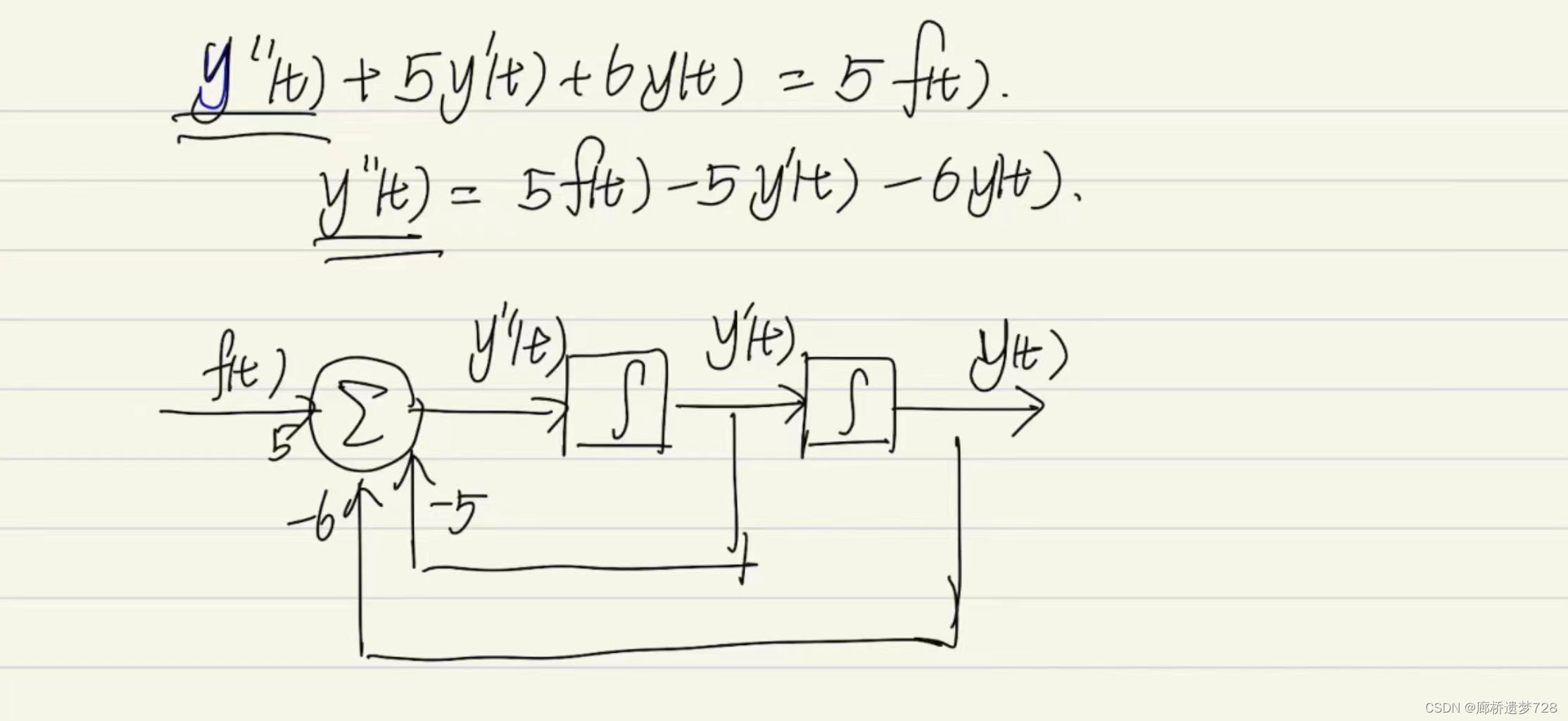







 本文介绍了如何通过微分方程建立LTI系统的数学模型,以RLC电路为例,并探讨了相似系统的概念。同时,通过模拟框图和中间变量法,展示了如何将微分方程转化为直观的图形表示,特别适用于处理输入带微分的常微分方程.
本文介绍了如何通过微分方程建立LTI系统的数学模型,以RLC电路为例,并探讨了相似系统的概念。同时,通过模拟框图和中间变量法,展示了如何将微分方程转化为直观的图形表示,特别适用于处理输入带微分的常微分方程.

















 1367
1367

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








