【金融量化分析】#期权相关定价方法与代码表达

期权主要使用的定价方法有偏微分方程法、鞅方法和数值方法。而数值方法又包括了二叉树方法、有限差分法和蒙特卡洛模拟方法。

想了解下不？

不想？滚

想，那得先知道 Black-Scholes 期权定价公式

Black-Scholes 期权定价公式（偏微分方程SDE）

简单推导期权定价模型：https://zhuanlan.zhihu.com/p/399851702

说人话就是：模型在推导过程中运用到了一个很重要的微分方程：

其中，式子中的 f 表示看涨期权价格，S表示期权基础资产的价格，r为连续复利的无风险收益率，σ为基础资产价格百分比变化(收益率)的波动率，t是时间变量。

欧式看涨期权

欧式看跌期权

L=K(不同版本的表达)

其中

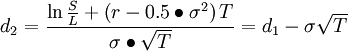
Code:

function Call = blsprice(S,K,r,T,sigma)
% BS formula for European call pricing

d1 = (1./(sigma.*sqrt(T))).*( log(S/K) + (r+sigma.^2/2).*T);
d2 = d1 - sigma.*sqrt(T);
Z1 = normcdf(d1,0,1);
Z2 = normcdf(d2,0,1);
Call = Z1*S - Z2*K*exp(-r*T);
end

python代码实现

import numpy as np
from scipy.stats import norm
 
def call_BS(S,K,sigma,r,T):
    '''用bs模型计算欧式看涨期权价格
    S 期权基础资产价格
    K 期权执行价格
    sigma 基础资产价格百分比变化（收益率）的年化波动率
    r 无风险收益率
    T 期权合约剩余年限
    '''
    d1 = (np.log(S/K) + (r + pow(sigma,2)/2)*T) / (sigma*np.sqrt(T))
    d2 = d1 - sigma*np.sqrt(T)
    return S*norm.cdf(d1) - K*np.exp(-r*T)*norm.cdf(d2)<