共轭函数

共轭函数

共轭函数的定义：

设函数$f:R^n \rightarrow R$，定义函数$f^*:R^n \rightarrow R$为：

$$f^*(y)=\sup_{x \in \mathbf{dom}f}(y^Tx-f(x))$$
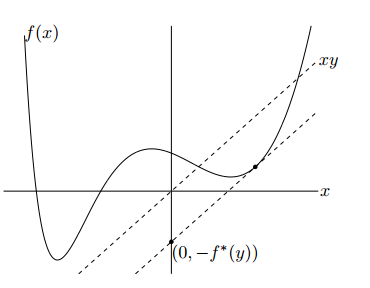
此函数称为函数 $f$的共轭函数。即函数$yx$和函数 $f(x)$之间差值的上确界。
如下图，两条虚线平行，函数 $f_1(x)=yx$是通过原点的一条直线,y是常数。下面的虚线交点
$(0,-f^*(y))$，即是两条平行线之间的y方向上的距离，即差值。

对偶范数

范数的对偶还是范数。
定义：
令$||\cdot||$是$\mathbf R^n$上 的范数。对应的对偶范数，用$||\cdot||$表示，定义为：

$$||z||_*=\text{sup} \{z^Tx | ||x|| \leq 1 \}$$
也可以写成：
$$\begin{equation} \max_x z^T x \\ s.t. ||x|| \leq 1 \end{equation}$$
因为范数具有非负性，因此我们也可以写成：
$$||z||_*=\text{sup} \{z^Tx | ||x|| \leq 1 \}$$

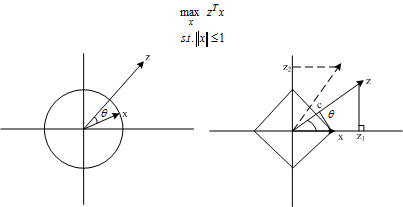
左图表示 $l2$范数对偶的示意图，很容易理解，当向量 $z$和$x$同方向时，两个向量的内积最大，即
$z^Tx=<z,x>=|z||x|\cdot cos \theta=|z|=||z||_2$

右图表示$l_1$范数对偶的示意图，当向量$z$在实线位置,两个向量的内积最大时，向量$x$取$(1,0)$(对于二维情况).则：
$z^Tx=<z,x>=|z||x|\cdot cos\theta=|z|\cdot cos\theta=z_1$
当向量$z$在虚线位置时：
$z^Tx=<z,x>=|z||x|\cdot cos\theta=|z|\cdot cos\theta=z_2$
故：
$z^Tx=max(z_1,z_2)=||z||_{\infty}$
即： $l2$范数的对偶范数还是$l2$范数，$l1$的对偶范数是$l\infty$范数 ;
即满足：如果$l_p$核$l_q$互为对偶范数，那么：

$$\frac{1}{p} + \frac{1}{q} = 1$$

范数的共轭函数

令$||\cdot||$表示$\mathbf R^n$上的范数，其对偶范数为$||\cdot ||_*$,那么函数$f(x)=||x||$的共轭函数为：

$$\begin{equation} f^*(y)= \begin{cases} 0 &||y||_* \leq 1 \\ \infty & 其他情况 \end{cases} \end{equation}$$
即范数的共轭函数是对偶范数的单位球的示性函数，即范数定义的单位球内值为0，在单位球外值为无穷大。对于损失函数来说，在单位球内损失函数为0，相当于一个ball约束，而在单位球外会导致损失函数无穷大，是不可取的。

证明：对于上左图，即对于$l2$范数的对偶，如果$||y||_*>1$，根据对偶范数的定义，存在$z\in \mathbf R^n，||z|| \leq 1$，使得$y^T z >1$。（这里的$y$对应上图的$z$,而$z$对应$x$，从图中可以看到$||z||\leq 1$即表示单位球形区域，要使得$||y||_* >1$，则一定满足$||y||>1$,一个大于1一个小于1，很自然存在$y,z$，满足$y^Tz>1$）。取$x=tz$，并令$t \rightarrow \infty$，可得：

$$y^Tx-||x||=t(y^Tz-||z||) \rightarrow \infty$$
即 $f^*(y)=\infty$，没有上界。反之，若 $||y||_* \leq 1$,对于任意的 $x$，有$y^T \leq ||x||y||_*$，即对任意 $x$，y^Tx-||x|| \leq 0$。因此，$x=0 $处，函数$y^Tx-||x||$达到最大值0.
可以通过下面的图进行一维情况的简单描述：

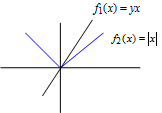
当 $y>1$时，即直线的斜率大于1时，则两个函数的差值为 $\infty$，两个函数都延伸到无穷远。当 $y\leq1$，函数 $f_1(x)$在函数 $f_2(x)$的下面，并且相交，因此最大y方向上的距离为0. 对于 $y<-1$和 $y\geq -1$具有类似的结论。

范数的平方的共轭函数：
函数:

$$f(x)=\frac{1}{2} ||x||^2$$
其共轭函数为：
$$f^*(y)=\frac{1}{2}||y||_*^2$$

参考文献：
1 Convex Optimization_Stephen Boyd.pdf
2. 摘自：凸优化_王书宁译, 第三章 凸函数， 第3.3小节共轭函数的例3.26(102页)。